动态规划？马尔可夫的计算美学

随机过程

随机游走

马尔可夫模型

马尔可夫过程

马尔可夫过程（Markov Process）是一类随机过程。它的原始模型马尔可夫链，由俄罗斯数学家Andrey Markov于1907年提出。该过程具有如下特性：在已知目前状态的条件下，它未来的演变不依赖于除目前状态以外的以往的演变。

换句话说，每个状态的转移只依赖于之前的 $n$ 个状态，这个过程被称为 $n$ 阶的马尔可夫过程， $n$ 是影响转移状态的数目。显然， $AR(p)$ 模型就是假设数据演变满足 $p$ 阶马尔可夫过程。

马尔可夫链

当取马尔可夫模型的阶 $n=1$ 时，得到的一阶马尔可夫过程就是原始的马尔可夫链（Markov Chain）。这表明每一个状态的转移只依赖于其之前的那一个状态，这种性质也叫作马尔可夫性质。其数学表达如下：

$P(X_{t+1} \mid X_0,...,X_{t-2}, X_{t-1}, X_{t} ) = P(X_{t+1} \mid X_{t})$

Note: 当我们谈起马尔可夫链时，一般就是指一阶马尔科夫过程。也有 $n$ 阶马尔可夫链的说法，这与 $n$ 阶马尔可夫过程的意思等价。

根据马尔科夫性质，如果我们求出系统中任意两个状态之间的转换概率，那么就确定了一个马尔科夫模型。

以股市模型为例，设有三种状态：牛市（Bull market）, 熊市（Bear market）和横盘（Stagnant market）。每一个状态都以一定的概率转化到下一个状态。比如，牛市以 0.025 的概率转化到横盘的状态。
可以绘制该示例的概率图如下：

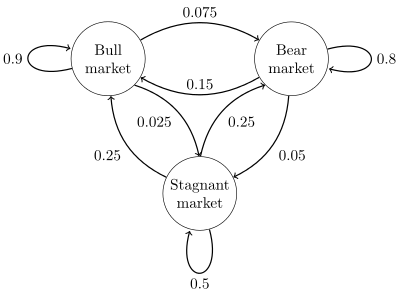
股市模型的马尔可夫链

上面这个状态概率转化图可以以矩阵的形式表示。
定义矩阵 $P$ 某一元素 $P_{i,j}=P(j|i)$ ，表示从状态 $i$ 转化到状态 $j$ 的概率，然后定义牛市为状态0，熊市为状态1, 横盘为状态2.。这样我们得到了该马尔科夫模型的状态转移矩阵：

$P=\left( \begin{array}{ccc} 0.9&0.075&0.025 \\ 0.15&0.8& 0.05 \\ 0.25&0.25&0.5 \end{array} \right)$

当对每个状态给定初始概率 $\pi_0=[\pi_0(0),\pi_0(1),\pi_0(2)]^T$ ，例如假设当前股市的概率分布为： $\pi_0=[0.3,0.4,0.3]^T$ ，即30%概率的牛市，40%概率的熊盘与30%的横盘。那么经过一次转移之后得到 $\pi_1=\pi_0P$ ，如此计算下去， $\pi_n=\pi_0P^{n}$ .

实验证明，当 $n$ 足够大时， $\pi_n$ 趋于稳定。不仅如此，选取不同的初始状态 $\pi_0$ ，最后的 $\pi_n$ 也趋于相同的值，这说明收敛的行为和初态无关，而是由概率转移矩阵 $P$ 决定的。这就是马尔科夫链的收敛性质。

平稳分布

马尔科夫链的收敛性质更进一步可以描述为：如果一个非周期的马尔科夫链有状态转移矩阵 $P$ ，并且它的任何两个状态是连通的，则：

$\lim_{n \to \infty}P^n = \left( \begin{array}{ccc} \pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\ \pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\ \ldots&\ldots&\ldots&\ldots&\ldots \\ \pi(1)&\pi(2)&\ldots&\pi(j)&\ldots \\ \ldots&\ldots&\ldots&\ldots&\ldots \end{array} \right)$