MLA 多头潜在注意力 | DeepSeek 技术拆解

本文对读者略有要求，需要对注意力机制事先就有些许了解，本站也做了相关的记录和它在线性化上的努力的收集. 👉注意力机制及其线性化之路 | SLie’s Blog | 琴弦之轮

KV Cache

MHA 即 Multi-Head Attention，多头注意力机制，是 Transformer 的核心机制，我们想必对其已经谈不上陌生了。在其线性化之路中，我们关注的是它的时空复杂度的优化，主要是希望在训练和推理阶段，其计算复杂度能从原来的二次复杂性降低到线性的 $\mathcal O(n)$ 级。而 MHA 在 LLM 中的应用已经充分印证了其强大的能力，LLM 得以成功也与 Scaling Law （参数量越大性能越好）密不可分。也因此，在训练一个大语言模型时，我们并不会对训练过程中的时空复杂度有着过大的需求；但反过来，在推理过程中，我们希望相同长度的上下文能尽可能地在更小的缓存空间内进行，以实现更快的推理速度或者更大的吞吐总量。要实现这一点，我们就需要对 MHA 中的 KV Cache 进行优化。

能一张卡部署的，就不要跨多张卡；能一台机部署的，就不要跨多台机。这是因为“卡内通信带宽 > 卡间通信带宽 > 机间通信带宽”，由于“木桶效应”，模型部署时跨的设备越多，受设备间通信带宽的的“拖累”就越大。

现如今的 LLM 都是 Decoder-only 的，所以实际上上采用的 MHA 是 Masked 的，换句话说是一种 Causal Attention。它使得第 $t+1$ 个 token 的输出只依赖前 $t$ 个token，而与未来的 token 无关。写成公式就是下面这样：

$\begin{gathered} \boldsymbol{o}_t = \left[\boldsymbol{o}_t^{(1)}, \boldsymbol{o}_t^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\right] \\[10pt] \boldsymbol{o}_t^{(s)} = Attention\left(\boldsymbol{q}_t^{(s)}, \boldsymbol{k}_{\leq t}^{(s)} ,\boldsymbol{v}_{\leq t}^{(s)}\right)\triangleq\frac{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)\boldsymbol{v}_i^{(s)}}{\sum_{i\leq t}\exp\left(\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top}\right)} \\[15pt] \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\ \boldsymbol{k}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d\times d_k} \\ \boldsymbol{v}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d\times d_v} \end{gathered}$

其中，第 $t$ 个 token 的第 $s$ 个注意力头的输出表示为 $\boldsymbol{o}_t^{(s)}$ ，共有 $h$ 个注意力头，所有向量这里用行向量表示。

可见，只要我们将输入至今的 token 的所有 key 和 value，并增量式地继续存储下去，那么每新来一个 token 我们都可以基于已有的结果继续计算（推理）下去，这就是 KV Cache。

一个最直观的想法自然就是从所谓的“多头”中去优化，因为每多一个“头“就多一份参数 $\boldsymbol{W}_k^{(s)},\boldsymbol{W}_v^{(s)}$ 的存储。所以接下来我们要介绍的优化方案，包括 MQA、GQA、以及 DeepSeek v2 & v3 中使用的 MLA 都是在这个思路上继续的。

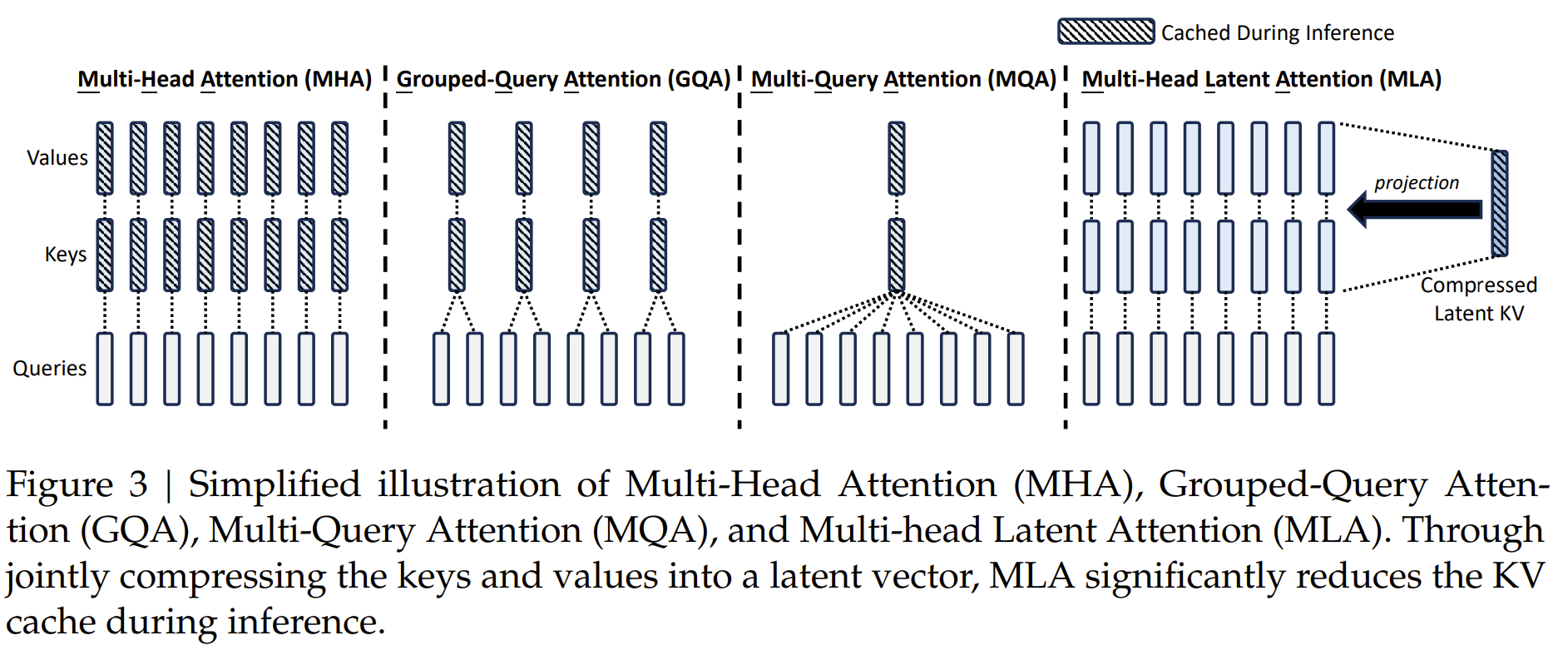
图源：DeepSeek v2 原论文

MQA

MQA (Multi-Query Attention)，是减少 KV Cache 的一次非常朴素的尝试，在2019年首次在论文《Fast Transformer Decoding: One Write-Head is All You Need》中被提出。

MQA的思路很简单，前面所给出的图示中也能够很明显地看出来，那就是直接让所有 Attention Head 都共享同一个K、V，用公式来说，就是取消 MHA 所有 $\boldsymbol{k},\boldsymbol{v}$ 的上标 $^{(s)}$ .

很明显，MQA直接将KV Cache减少到了原来的 $1/h$ ，这是非常可观的，单从节省显存角度看已经是天花板了。效果方面，目前看来大部分任务的损失都比较有限，且MQA的支持者相信这部分损失可以通过进一步训练来弥补回。此外，注意到MQA由于共享了K、V，将会导致Attention的参数量减少了将近一半，而为了模型总参数量的不变，通常会相应地增大FFN/GLU的规模，这也能弥补一部分效果损失。

使用MQA的模型包括PaLM、StarCoder、Gemini等。

GQA

MQA 对 KV Cache 的压缩直觉来讲确实有点严重，特别是 $h$ 较大的时候，可能会影响模型的学习效率以及最终效果。为此，一个 MHA 与 MQA 之间的过渡版本GQA（Grouped-Query Attention）应运而生，出自论文《GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints》.

GQA的思想也很朴素，它就是将所有 Head 分为 $g$ 个组（ $g$ 可以整除 $h$ ），每组共享同一对K、V，如下列公式所示。

$\begin{gathered} \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\ \boldsymbol{k}_i^{\color{red}{(\lceil sg/h\rceil)}} = \boldsymbol{x}_i\boldsymbol{W}_k^{\color{red}{(\lceil sg/h\rceil)}}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{\color{red}{(\lceil sg/h\rceil)}}\in\mathbb{R}^{d\times d_k} \\ \boldsymbol{v}_i^{\color{red}{(\lceil sg/h\rceil)}} = \boldsymbol{x}_i\boldsymbol{W}_v^{\color{red}{(\lceil sg/h\rceil)}}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{\color{red}{(\lceil sg/h\rceil)}}\in\mathbb{R}^{d\times d_v} \end{gathered}$

仍然以上面的示意图为例，图中 $h=8$ ， $g=4$ ，所以就有 $h/g=2$ 个 Head 为一组。当 $s=1,2$ 时，上标 $\lceil sg/h\rceil=1$ ，即他们俩被分为同一组，以此类推。在计算时属于同一组的 KV 是共享的。值得一提的是，当 $g=1$ 时 GQA 就退化成了 MHA，当 $g=h$ 时 GQA 就变成了 MQA。

虽然 GQA 的压缩率不如 MQA，但同时也提供了更大的自由度，效果上更有保证。

GQA最知名的使用者，大概是Meta开源的LLAMA2-70B，以及LLAMA3全系列，此外使用GQA的模型还有TigerBot、DeepSeek-V1、StarCoder2、Yi、ChatGLM2、ChatGLM3等。

MLA

MLA（Multi-head Latent Attention）由 DeepSeek v2 的技术报告首次提出，报告里是从低秩投影的角度引入 MLA 的，而苏剑林苏神对 MLA 进行解读时，考虑到了 MLA 的另一个解释的视角（苏神认为这个视角可能更接近MLA的本质），即“MLA 是 GQA 的一般化形式”。

低秩压缩视角

DeepSeek 为了解决 KV Cache 问题进而引入了MLA，其核心想法是将 $\boldsymbol{k},\boldsymbol{v}$ 联合起来，一并通过低秩投影压缩（由下投影矩阵 $\boldsymbol W_c$ 完成，原论文中写作 $\boldsymbol W^{DKV}$ ，Down-projection matrix）到某个潜在空间（Latent Space）中得到一个潜在KV向量 $\boldsymbol c$ 。

如果想要还原出 $\boldsymbol{k},\boldsymbol{v}$ ，可以分别利用两个上投影矩阵（Up-projection matrices，原论文写作 $\boldsymbol W^{UK}$ 和 $\boldsymbol W^{UV}$ ）作用到 $\boldsymbol c$ 上以还原。具体来说 QKV 由下式给出。

$\begin{gathered} \boldsymbol{q}_i^{(s)} = \boldsymbol{x}_i\boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_q^{(s)}\in\mathbb{R}^{d\times d_k}\\ \boldsymbol{k}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_k},\quad \boldsymbol{W}_k^{(s)}\in\mathbb{R}^{d_c\times d_k} \\ \boldsymbol{v}_i^{(s)} = \boldsymbol{c}_i\boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_v},\quad \boldsymbol{W}_v^{(s)}\in\mathbb{R}^{d_c\times d_v} \\[10pt] \boldsymbol{c}_i = \boldsymbol{x}_i \boldsymbol{W}_c\in\mathbb{R}^{d_c},\quad \boldsymbol{W}_c\in\mathbb{R}^{d\times d_c} \end{gathered}$

GQA增强视角

回看 GQA 的核心做法：首先将向量对半分为两份分别作为K、V，然后每一份又均分为 $g$ 组，每组复制 $h/g$ 次，以此来“凑”够 $h$ 个 Attention Head 所需要的K、V。

实际上，分别针对 K 和 V 的 $g$ 个组进行线性投影（分别有 $g$ 个投影矩阵，共 $2g$ 个），等价于使用一次线性投影将 token 向量 $\boldsymbol{x}_i$ 投影生成出维度是 $g(d_k+d_v)$ 的新向量，然后再对新向量进行拆分，最后对每一份复制 $h/g$ 次。如果我们把最后这个复制的过程也替换成一般的线性变换，也就是再通过一次线性投影将维度是 $g(d_k+d_v)$ 的新向量投影成维度是 $h(d_k+d_v)$ 的新向量，然后再拆开成每一个 Attention Head 所需的 K、V。而这，其实就是 MLA 的处理方案，通过将分割、复制操作（可以视为某种更特殊而又简单的线性变换）替换成更一般的线性变换，以增强模型的能力。

更形式化一点，我们将上面的描述用公式表达，将 GQA 的所有 $g$ 个组的 $\boldsymbol{k},\boldsymbol{v}$ 拼起来视作某个向量 $\boldsymbol c$ 的话，就能得到：

$\underbrace{\left[\boldsymbol{k}_i^{(1)},\cdots,\boldsymbol{k}_i^{(g)},\boldsymbol{v}_i^{(1)},\cdots,\boldsymbol{v}_i^{(g)}\right]}_{\boldsymbol{c}_i\in\mathbb{R}^{g(d_k+d_v)}} = \boldsymbol{x}_i \underbrace{\left[\boldsymbol{W}_k^{(1)},\cdots,\boldsymbol{W}_k^{(g)},\boldsymbol{W}_v^{(1)},\cdots,\boldsymbol{W}_v^{(g)}\right]}_{\boldsymbol{W}_c\in\mathbb{R}^{d\times g(d_k+d_v)}}$

由于 $d_c = g(d_k+d_v) < d$ 的，所以这个过程就是一个低秩投影（而“复制”的过程就是一个上投影）。也就是说，其实 GQA 所做的事情，也是在做一个低秩投影！

事实上，MLA的本质改进不是低秩投影，而是低秩投影之后的工作，包括重新定义所需缓存的向量以及在新定义下如何处理 RoPE 的问题。

矩阵参数的吸收化简

如前文所述，MLA 在低秩投影后通过不同的上投影矩阵（替换掉GQA的复制操作）增强了模型能力。但是这样一来，因为使用了不同的投影，所以 KV Cache 里我们仍然需要存储每个 Head 的 $\boldsymbol{k},\boldsymbol{v}$ （大小又恢复成跟 MHA一样大了），这违背了GQA的初衷。为此，MLA 结合 Dot-Attention 的具体形式，通过一个简单但不失巧妙的恒等变换来规避这个问题。

我们知道计算注意力分数需要计算 $\boldsymbol{q} \boldsymbol{k}^{\top}$ ，如果用 MLA 的投影策略将其写开：

$\boldsymbol{q}_t^{(s)} \boldsymbol{k}_i^{(s)}{}^{\top} = \left(\boldsymbol{x}_t\boldsymbol{W}_q^{(s)}\right) \left(\boldsymbol{c}_i\boldsymbol{W}_k^{(s)}\right){}^{\top} = \boldsymbol{x}_t\left(\boldsymbol{W}_q^{(s)}\boldsymbol{W}_k^{(s)}{}^{\top}\right)\boldsymbol{c}_i^{\top}$

作者指出，我们可以把针对第 $s$ 个头的 key 的上投影矩阵 $\boldsymbol{W}_k^{(s)}$ 包含进前面针对 query 的矩阵 $\boldsymbol{W}_q^{(s)}$ 里面去，也就是把 $\boldsymbol{W}_q^{(s)}\boldsymbol{W}_k^{(s)}{}^{\top}$ 这个整体看作是 Q 的投影矩阵，这样一来这一步的计算可以化简为 $\boldsymbol{q}_t^{(s)} \boldsymbol{c}^{\top}$ （理论上只有在无限精度下这种合并才能成立）。

而针对第 $s$ 个头的 value 的上投影矩阵 $\boldsymbol{W}_v^{(s)}$ 实际上也可以合并到注意力层的输出层的投影矩阵里去（得到 $\boldsymbol{o}_t = \left[\boldsymbol{o}_t^{(1)}, \boldsymbol{o}_t^{(2)}, \cdots, \boldsymbol{o}_t^{(h)}\right]$ 之后通常还要再过一层线性层得到输出）。