基本介绍 1986 年,Rumelhart、Hinton 和 Williams 首次提出了自编码器 (Autoencoder,AE),旨在学习以尽可能低的误差重建 输入观测值x i \boldsymbol x_i x i
Rumelhart D E , Hinton G E , Williams R J .Learning Internal Representation by Error Propagation[M]. 1986.
定义与架构 Definition : An autoencoder is a type of algorithm with the primary purpose of learning an “informative” representation of the data that can be used for different applicationsa by learning to reconstruct a set of input observations well enough.
上述定义是 Bank, D., Koenigstein, N., and Giryes, R. 在他们的文章 Autoencoders, https://arxiv.org/abs/2003.05991 中给出的自编码器的定义。
我们需要明确的是,自编码器是一种无监督学习/自监督学习 方法,而它学习到的潜在表示 蕴含有输入数据的大量丰富的信息,可以用于各种其他下游任务。所以具体来说自编码器还属于一类表示学习 方法,生成式自监督学习方法 ,还可以说,它实现了一种降维 的作用。
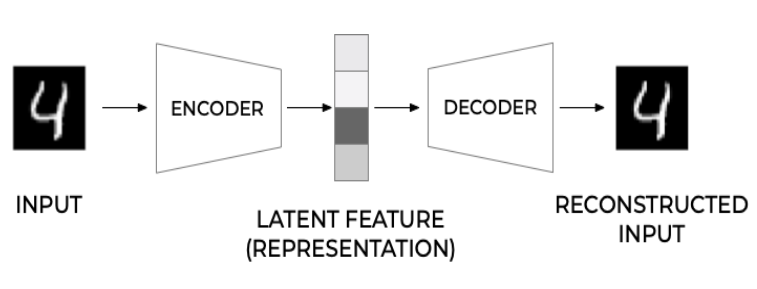
一个自编码器的经典架构如下图所示:
我们将输入的数据x \bf x x E ( ⋅ ) E(·) E ( ⋅ ) 1 h \bf h h D ( ⋅ ) D(·) D ( ⋅ ) x ~ \tilde{\bf x} x ~ x ~ = D ( h ) = D ( E ( x ) ) \tilde{\bf x}=D(\mathbf h)=D(E(\mathbf x)) x ~ = D ( h ) = D ( E ( x ))
为了使得重建的数据与原输入数据尽可能地相似,自动编码器最常用的损失函数就是均方误差 (MSE:mean squared error) 或二进制交叉熵 (BCE:binary cross-entropy),具体取决于输入数据的性质。
在大多数经典架构中,Encoder 和 Decoder 都是神经网络,可以用成熟的梯度下降法进行训练。自然,这些可以很容易地用现有的深度学习框架(TensorFlow 或 PyTorch)实现。
注1:这里的潜在特征(Latent Feature) 亦可以叫做潜在编码(Latent Code)、潜在向量(Latent Vector),或是潜在表示(Latent Represetation) 也可直接叫做表示(Represetation),甚至嵌入(Embedding)。
深度学习中对经过神经网络处理后得来的、蕴含了输入数据的丰富信息的“变量”进行了许多不同的命名,但是它们的本质是一样的。
类比PCA 我们知道PCA是机器学习中最常见的数据降维算法,也属于无监督学习范畴。x \bf x x W W W z \bf z z W T z W^T\bf z W T z x ~ \tilde{\bf x} x ~ x \bf x x x ~ \tilde{\bf x} x ~
事实上,机器学习中PCA可以通过对协方差矩阵 进行特征值分解 求得解析解 (即 变换矩阵W W W
其实,PCA还可以从深度学习的角度来理解——可以将PCA理解为一类特殊的自编码器的训练过程,编码器和解码器由互为转置的权重矩阵W , W T W,W^T W , W T 瓶颈层 (Bottleneck Layer),训练的方式就是利用梯度下降 来极小化x \bf x x x ~ \tilde{\bf x} x ~
前馈自编码器 前馈自编码器 (Feed-Forward Autoencoder,FFA)也可以称为普通自编码器(Vanilla Autoencoder)或深度自编码器(网络层堆叠较多的话)。它由具有特定结构的密集神经网络层组成。
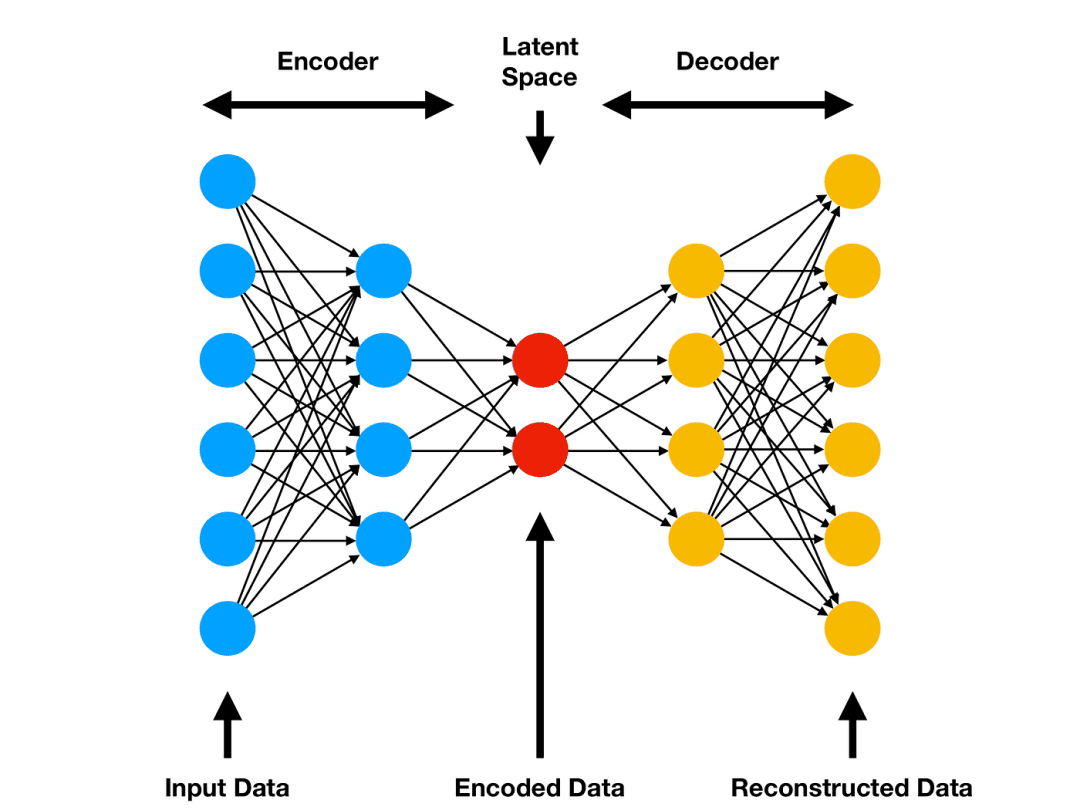
下图展现的是由全连接层构成的前馈自编码器,图源: Amor, “Comprehensive introduction to Autoencoders,” ML Cheat Sheet, 2021
经典的 FFA 架构层的数量为奇数 (尽管不是强制性要求),并且与中间层对称 。
具体地,每经过一层网络,新一层网络的神经元数量都会有所下降。中间层有着最少的神经元,这就是前面提到的「瓶颈」,我们也是在这一层得到其潜在表示的。随后对称地 ,每一层的神经元数量开始上升。在几乎所有的实际应用中,中间层之后的网络层都是中间层之前的镜像版本 。中间层在及之前的所有层就构成了所谓的编码器 。
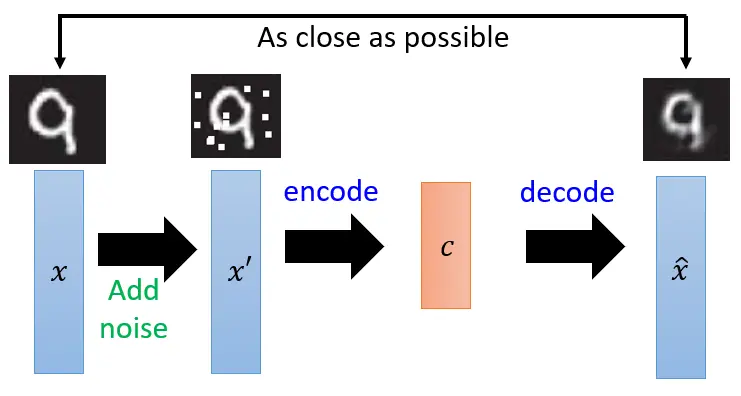
降噪自编码器 降噪自编码器 (Denoising Autoencoder2 )可以使学习到的低维表示具备更高的鲁棒性 ,因为该方法让模型在学习重构数据的同时也学习到了如何去除数据中的噪声。
具体原理是先在原始数据中添加噪声,然后将加噪的数据输入到自编码器中,要求输出的重构数据要尽可能与原来未加噪的数据接近。
注2:Vincent,Pascal, et al. “Extracting and composing robust features with denoising autoencoders.” ICML,2008.
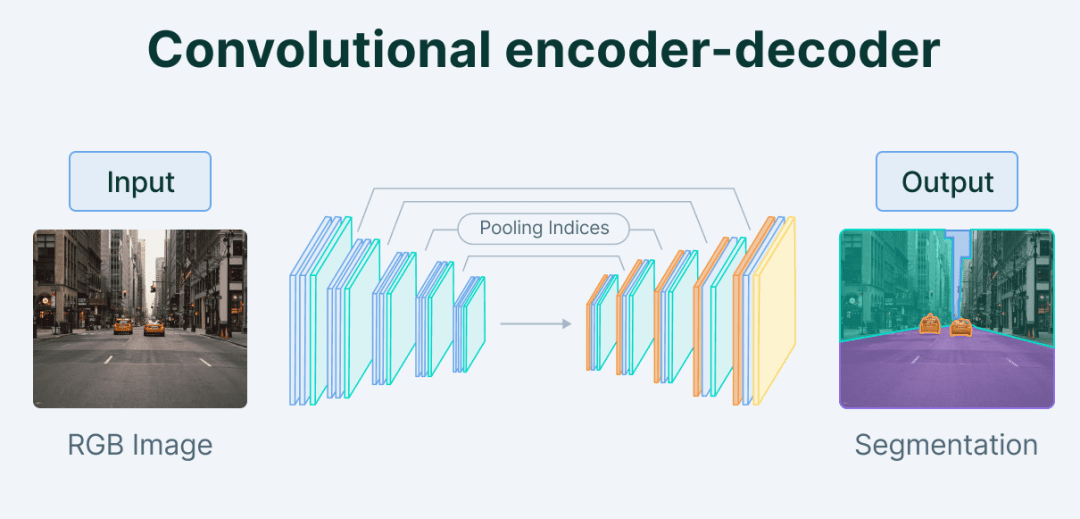
卷积自编码器 卷积自编码器 (Convolutional Autoencoder,CAE)在编码器和解码器中利用卷积层,使其适用于处理图像数据 。通过利用图像中的空间信息,CAE可以比普通自动编码器更有效地捕获复杂的模式和结构,并完成图像分割等任务。
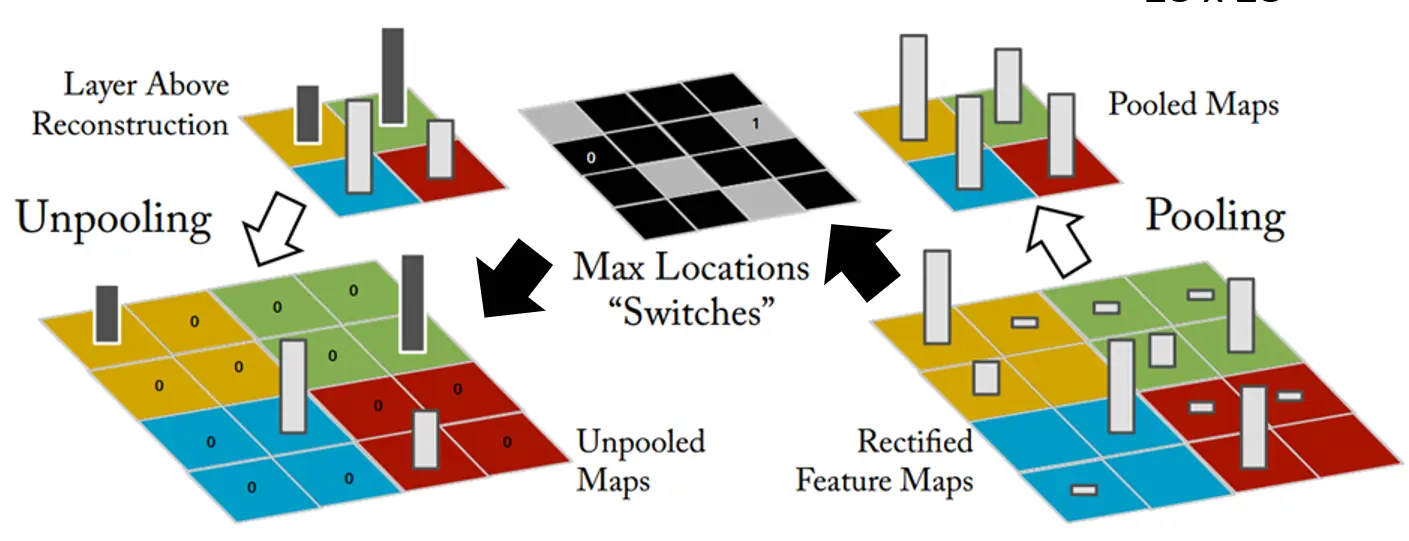
和CNN一样,前期的编码过程自编码器需要对原始图像进行卷积和池化等操作。而后续的解码过程,相应地需要实现 反池化“Unpooling ” 和 反卷积“Deconvolution ” 操作。
UnPooling 我们知道做池化操作时,比如利用2 × 2 2\times2 2 × 2 2 2 2 16 × 16 16\times16 16 × 16 max pooling 。那么特征图将被分成4 4 4 4 × 4 4\times4 4 × 4
以右下角的特征图为例,它被分成4 4 4
在卷积自编码器中,一种常见的 Unpooling 方法是 在编码时记录下选取元素的位置 ,然后在重建时扩大特征图并在对应位置填上最大值 ,其余位置置零。
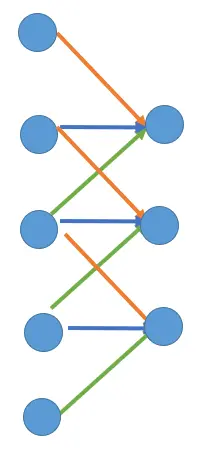
Deconvolution 为了理解反卷积,我们以一维数据的卷积为例探讨其本质行为。
Convolution Deconvolution
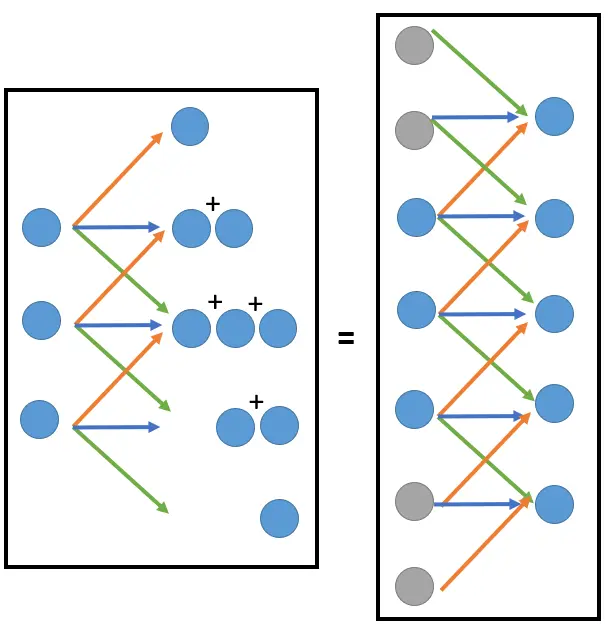
如上图所示,以大小是5 5 5 3 3 3 1 1 1 3 3 3 加权求和 得到输出特征图的其中一个元素,然后滑动一个单位,下一组3 3 3 共享权重 (图中的红蓝绿三条线)地再一次加权求和,以此类推。
最终我们得到大小是3 3 3 5 5 5
也就是说,Deconvolution某种程度上也是一种Convolution 。
稀疏自编码器 稀疏自编码器 (Sparse Autoencoders)通过向损失函数添加稀疏性惩罚项约束 强迫潜在表示具备稀疏性,从而实现更高效、更稳健的特征提取。
具体来说,常使用的惩罚项由 KL散度 给出。
待更:稀疏自编码器-CSDN博客 [自编码器] [稀疏自编码器] Auto Encoder原理详解 - virter - 博客园 (cnblogs.com) Introduction to autoencoders. - jeremyjordan.me Machine Learning|稀疏编码和矩阵分解_华北小龙虾的博客-CSDN博客 『ML笔记』深入浅出字典学习1(Dictionary Learning)-CSDN博客
事实上,从它的名字——稀疏自编码器 就能得出,其渊源是机器学习中的稀疏编码和字典学习 领域。详见本站文章:
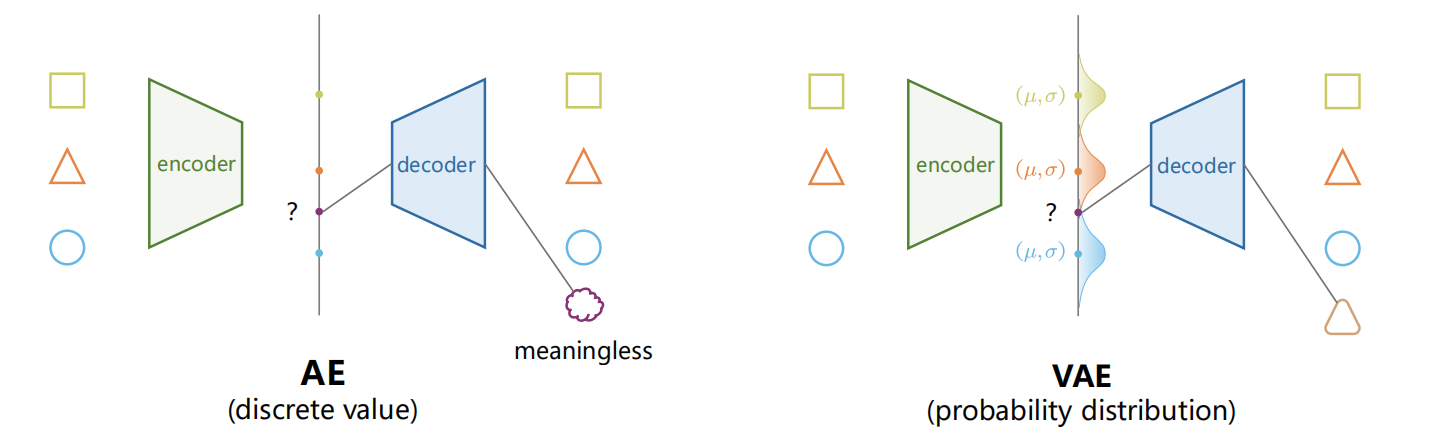
变分自编码器 当我们欲将训练的解码器看作是某种”生成器 “,使得潜在表示空间中随机生成的向量也能解码出某种图像或与原数据相同类型的数据时,原始的自编码器算法就很难有效、可控地完成任务了。这是因为原始的自编码器 Latent Space 往往是离散的,无法从该空间中任意采样并 decode 出有意义的输出(如下图所示)。
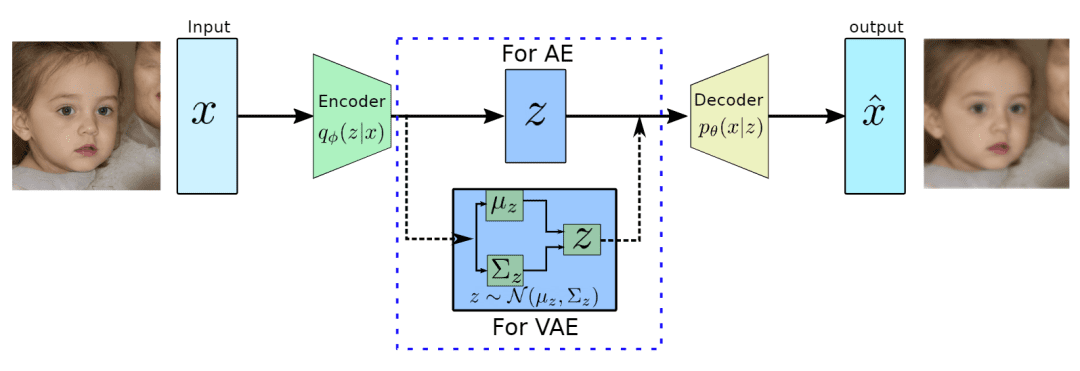
变分自编码器 (Variational Auto-Encoders,VAE)作为深度生成模型 的一种形式,是由 Kingma 等人于 2014 年提出的基于变分贝叶斯(Variational Bayes,VB)推断 的生成式网络结构。与传统的自编码器通过数值的方式描述潜在空间不同,它以概率 的方式描述对潜在空间的观察,在数据生成方面表现出了巨大的应用价值。
VAE一经提出就迅速获得了深度生成模型领域广泛的关注,并和生成对抗网络 (Generative Adversarial Networks,GAN)被视为无监督式学习领域最具研究价值的方法之一,在深度生成模型领域得到越来越多的应用。
变分推导
如上图所示,VAE 的目标是希望将输入x \mathbf x x z \mathbf z z p θ ∗ ( z ) p_{\theta^*}(\mathbf z) p θ ∗ ( z ) z ( i ) \mathbf z^{(i)} z ( i ) p θ ∗ ( x ∣ z = z ( i ) ) p_{\theta^*}(\mathbf x\vert \mathbf z=\mathbf z^{(i)}) p θ ∗ ( x ∣ z = z ( i ) ) x ( i ) \mathbf x^{(i)} x ( i ) θ ∗ \theta^* θ ∗ p p p
为了优化得到最优参数,我们考虑通过极大似然估计(MLE):
θ ∗ = arg max θ ∏ i = 1 n p θ ( x ( i ) ) = arg max θ ∑ i = 1 n log p θ ( x ( i ) ) \begin{aligned} \theta^{*} &= \arg\max_\theta \prod_{i=1}^n p_\theta(\mathbf{x}^{(i)})\\ & = \arg\max_\theta \sum_{i=1}^n \log p_\theta(\mathbf{x}^{(i)}) \end{aligned} θ ∗ = arg θ max i = 1 ∏ n p θ ( x ( i ) ) = arg θ max i = 1 ∑ n log p θ ( x ( i ) )
这里待优化参数θ \theta θ 似然函数 ”使用的是x \bf x x 边缘似然 ,因为它是仅与参数θ \theta θ x \bf x x θ \theta θ p θ ( x ∣ z ) p_\theta(\mathbf x\vert\mathbf z) p θ ( x ∣ z ) 条件似然 ,这个概率还与隐变量z \bf z z z \bf z z θ \theta θ z \bf z z θ \theta θ x \bf x x
上式中对应的似然函数展开来如下式所示,不幸的是我们很难遍历所有可能的z \bf z z
p θ ( x ) = ∫ p θ ( x , z ) d z = ∫ p θ ( x ∣ z ) p θ ( z ) d z p_\theta(\mathbf x)=\int p_\theta(\mathbf {x},\mathbf {z})\;\mathrm d\mathbf z=\int p_\theta(\mathbf {x}\vert\mathbf {z})p_\theta(\mathbf {z})\;\mathrm d\mathbf z p θ ( x ) = ∫ p θ ( x , z ) d z = ∫ p θ ( x ∣ z ) p θ ( z ) d z
另一方面,真实分布下的后验概率p θ ∗ ( z ∣ x ) p_{\theta^*}(\mathbf z\vert \mathbf x) p θ ∗ ( z ∣ x ) p θ ( x ) p_\theta(\mathbf x) p θ ( x ) 变分推断(Variational Inference,VI) ,我们可以设计一种近似函数q ϕ ( z ∣ x ) q_{\phi}(\mathbf z\vert \mathbf x) q ϕ ( z ∣ x )
这个近似函数我们可以使用神经网络进行拟合,参数为ϕ \phi ϕ ϕ \phi ϕ D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) D_\text{KL}\big( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x})\big) D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) )
将其展开:
D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) = ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) p θ ( z ∣ x ) d z = ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) p θ ( x ) p θ ( z , x ) d z ; Because p ( z ∣ x ) = p ( z , x ) / p ( x ) = ∫ q ϕ ( z ∣ x ) ( log p θ ( x ) + log q ϕ ( z ∣ x ) p θ ( z , x ) ) d z = log p θ ( x ) + ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) p θ ( z , x ) d z ; Because ∫ q ( z ∣ x ) d z = 1 = log p θ ( x ) + ∫ q ϕ ( z ∣ x ) log q ϕ ( z ∣ x ) p θ ( x ∣ z ) p θ ( z ) d z ; Because p ( z , x ) = p ( x ∣ z ) p ( z ) = log p θ ( x ) + E z ∼ q ϕ ( z ∣ x ) [ log q ϕ ( z ∣ x ) p θ ( z ) − log p θ ( x ∣ z ) ] = log p θ ( x ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ) ) − E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) \begin{aligned} & D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) ) & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z} \vert \mathbf{x})} d\mathbf{z} & \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})p_\theta(\mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z \vert x) = p(z, x) / p(x)} \\ &=\int q_\phi(\mathbf{z} \vert \mathbf{x}) \big( \log p_\theta(\mathbf{x}) + \log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} \big) d\mathbf{z} & \\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z}, \mathbf{x})} d\mathbf{z} & \scriptstyle{\text{; Because }\int q(z \vert x) dz = 1}\\ &=\log p_\theta(\mathbf{x}) + \int q_\phi(\mathbf{z} \vert \mathbf{x})\log\frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{x}\vert\mathbf{z})p_\theta(\mathbf{z})} d\mathbf{z} & \scriptstyle{\text{; Because }p(z, x) = p(x \vert z) p(z)} \\ &=\log p_\theta(\mathbf{x}) + \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z} \vert \mathbf{x})}[\log \frac{q_\phi(\mathbf{z} \vert \mathbf{x})}{p_\theta(\mathbf{z})} - \log p_\theta(\mathbf{x} \vert \mathbf{z})] &\\ &=\log p_\theta(\mathbf{x}) + D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z})) - \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})}\log p_\theta(\mathbf{x}\vert\mathbf{z}) & \end{aligned} D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x )) = ∫ q ϕ ( z ∣ x ) log p θ ( z ∣ x ) q ϕ ( z ∣ x ) d z = ∫ q ϕ ( z ∣ x ) log p θ ( z , x ) q ϕ ( z ∣ x ) p θ ( x ) d z = ∫ q ϕ ( z ∣ x ) ( log p θ ( x ) + log p θ ( z , x ) q ϕ ( z ∣ x ) ) d z = log p θ ( x ) + ∫ q ϕ ( z ∣ x ) log p θ ( z , x ) q ϕ ( z ∣ x ) d z = log p θ ( x ) + ∫ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) p θ ( z ) q ϕ ( z ∣ x ) d z = log p θ ( x ) + E z ∼ q ϕ ( z ∣ x ) [ log p θ ( z ) q ϕ ( z ∣ x ) − log p θ ( x ∣ z )] = log p θ ( x ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z )) − E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) ; Because p ( z ∣ x ) = p ( z , x ) / p ( x ) ; Because ∫ q ( z ∣ x ) d z = 1 ; Because p ( z , x ) = p ( x ∣ z ) p ( z )
这样推导的好处时,我们把似然函数这一项log p θ ( x ) \log p_\theta(\mathbf{x}) log p θ ( x ) log p θ ( x ) \log p_\theta(\mathbf{x}) log p θ ( x ) 近似后验概率 的同时 最大化似然概率 。
最终得到 VAE 的损失函数:
L VAE ( θ , ϕ ) = − log p θ ( x ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x ) ) = − E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ) ) θ ∗ , ϕ ∗ = arg min θ , ϕ L VAE \begin{aligned} L_\text{VAE}(\theta, \phi) &= -\log p_\theta(\mathbf{x}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}\vert\mathbf{x}) )\\ &= - \mathbb{E}_{\mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x})} \log p_\theta(\mathbf{x}\vert\mathbf{z}) + D_\text{KL}( q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}) ) \\ \theta^{*}, \phi^{*} &= \arg\min_{\theta, \phi} L_\text{VAE} \end{aligned} L VAE ( θ , ϕ ) θ ∗ , ϕ ∗ = − log p θ ( x ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z ∣ x )) = − E z ∼ q ϕ ( z ∣ x ) log p θ ( x ∣ z ) + D KL ( q ϕ ( z ∣ x ) ∥ p θ ( z )) = arg θ , ϕ min L VAE
对于最终的损失,我们还可以将这两项分别理解为:最大化从潜在空间中重构出原数据的可能性 和 编码器与潜在空间分布的逼近 。
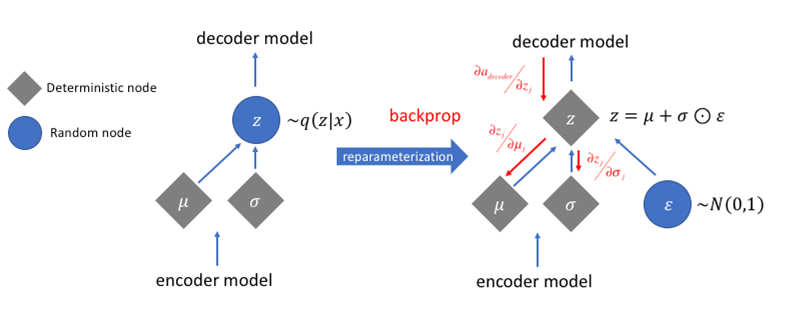
实现细节 在使用神经网络作为编码器(拟合函数q ϕ ( z ∣ x ) q_{\phi}(\mathbf z\vert \mathbf x) q ϕ ( z ∣ x ) z ∼ q ϕ ( z ∣ x ) \mathbf{z} \sim q_\phi(\mathbf{z}\vert\mathbf{x}) z ∼ q ϕ ( z ∣ x )
z ∼ q ϕ ( z ∣ x ( i ) ) = N ( z ; μ ( i ) , σ 2 ( i ) I ) z = μ + σ ⊙ ϵ , where ϵ ∼ N ( 0 , I ) ; Reparameterization trick. \begin{aligned} \mathbf{z} &\sim q_\phi(\mathbf{z}\vert\mathbf{x}^{(i)}) = \mathcal{N}(\mathbf{z}; \boldsymbol{\mu}^{(i)}, \boldsymbol{\sigma}^{2(i)}\boldsymbol{I}) & \\ \mathbf{z} &= \boldsymbol{\mu} + \boldsymbol{\sigma} \odot \boldsymbol{\epsilon} \text{, where } \boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I}) & \scriptstyle{\text{; Reparameterization trick.}} \end{aligned} z z ∼ q ϕ ( z ∣ x ( i ) ) = N ( z ; μ ( i ) , σ 2 ( i ) I ) = μ + σ ⊙ ϵ , where ϵ ∼ N ( 0 , I ) ; Reparameterization trick.
通常如果真的按照原来的分布来采样(并非标准正态分布),这样的采样数据是不可微的,亦即不能反传梯度,所以普遍采用重参数化技巧 (reparameterization trick )让模型能够把ϵ ∼ N ( 0 , I ) \boldsymbol\epsilon\sim\mathcal N(0,\mathbf I) ϵ ∼ N ( 0 , I )
NOTE: 其中的μ , σ \mu,\sigma μ , σ x x x
通常假设潜在空间的分布服从标准正态分布 ,即p θ ( z ) = N ( 0 , I ) p_\theta(z)=\mathcal{N}(0,\mathbf I) p θ ( z ) = N ( 0 , I ) x ( i ) x^{(i)} x ( i )
L ~ ( θ , ϕ ; x ( i ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + E ϵ ∼ p ( ϵ ) log p θ ( x ( i ) ∥ g ϕ ( ϵ , x ( i ) ) ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣ ∣ p θ ( z ) ) + 1 L ∑ l = 1 L log p θ ( x ( i ) ∣ z ( i , l ) ) = − 1 2 ∑ j = 1 J ( 1 + log σ ( i , j ) 2 − μ ( i , j ) 2 − σ ( i , j ) 2 ) + 1 L ∑ l = 1 L log p θ ( x ( i ) ∣ z ( i , l ) ) where z ( i , l ) = μ ( i ) + σ ( i ) ⊙ ϵ ( l ) , ϵ ( l ) ∼ N ( 0 , I ) \begin{aligned} \tilde{\mathcal{L}}(\theta, \phi; x^{(i)}) &= -D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z)) + \mathbb{E}_{\epsilon \sim p(\epsilon)} \log p_{\theta}(x^{(i)}\|g_{\phi}(\epsilon, x^{(i)})) \\ &= -D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z)) + \frac{1}{L} \sum_{l=1}^L \log p_{\theta}(x^{(i)}|z^{(i,l)}) \\ &= -\frac{1}{2} \sum_{j=1}^J \left(1 + \log \sigma^{(i,j)^2} - \mu^{(i,j)^2} - \sigma^{(i,j)^2} \right) + \frac{1}{L} \sum_{l=1}^L \log p_{\theta}(x^{(i)}|z^{(i,l)}) \\ \text{where } z^{(i,l)} &= \mu^{(i)} + \sigma^{(i)} \odot \epsilon^{(l)}, \epsilon^{(l)} \sim \mathcal{N}(0, \mathbf I) \end{aligned} L ~ ( θ , ϕ ; x ( i ) ) where z ( i , l ) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z )) + E ϵ ∼ p ( ϵ ) log p θ ( x ( i ) ∥ g ϕ ( ϵ , x ( i ) )) = − D K L ( q ϕ ( z ∣ x ( i ) ) ∣∣ p θ ( z )) + L 1 l = 1 ∑ L log p θ ( x ( i ) ∣ z ( i , l ) ) = − 2 1 j = 1 ∑ J ( 1 + log σ ( i , j ) 2 − μ ( i , j ) 2 − σ ( i , j ) 2 ) + L 1 l = 1 ∑ L log p θ ( x ( i ) ∣ z ( i , l ) ) = μ ( i ) + σ ( i ) ⊙ ϵ ( l ) , ϵ ( l ) ∼ N ( 0 , I )
其中,J J J z ∈ R J z\in\mathbb R^{J} z ∈ R J i i i L L L L L L 事实上,原官方实现对第二项直接采用 MSELoss 进行替代 。
Pytorch代码 此处给出使用 Pytorch 在 MNIST 数据集上训练 VAE 的简易实现代码,参考自 learn_vae/VAE/main.ipynb OxOOo .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 class VAE_Encoder (nn.Module): def __init__ (self, input_dim, hidden_dim, latent_dim ): super (VAE_Encoder, self).__init__() self.encoder = nn.Sequential( nn.Linear(input_dim, hidden_dim), nn.Tanh() ) self.fc_mu = nn.Linear(hidden_dim, latent_dim) self.fc_logvar = nn.Linear(hidden_dim, latent_dim) def forward (self, x ): h = self.encoder(x) return self.fc_mu(h), self.fc_logvar(h) class VAE_Decoder (nn.Module): def __init__ (self, input_dim, hidden_dim, latent_dim ): super (VAE_Decoder, self).__init__() self.decoder = nn.Sequential( nn.Linear(latent_dim, hidden_dim), nn.Tanh(), nn.Linear(hidden_dim, input_dim), nn.Sigmoid() ) def forward (self, z ): return self.decoder(z) class VAE (nn.Module): def __init__ (self, input_dim=784 , hidden_dim=500 , latent_dim=5 ): super (VAE, self).__init__() self.latent_dim = latent_dim self.encoder = VAE_Encoder(input_dim, hidden_dim, latent_dim) self.decoder = VAE_Decoder(input_dim, hidden_dim, latent_dim) def encode (self, x ): return self.encoder(x) def decode (self, z ): return self.decoder(z) def reparameterize (self, mu, logvar ): """ 重参数化技巧,先从标准正态分布中采样一个epsilon,然后根据隐变量分布的均值和方差,计算出隐变量. """ std = torch.exp(0.5 * logvar) epsilon = torch.randn_like(std, requires_grad=False ) return mu + epsilon * std def forward (self, x ): mu, logvar = self.encoder(x) z = self.reparameterize(mu, logvar) return self.decoder(z), mu, logvar device = torch.device("cuda" if torch.cuda.is_available() else "cpu" ) print (f"Using device: {device} " )model = VAE().to(device) def loss_function (x, recon_x, mu, logvar ): KLD = -0.5 * torch.sum (1 + logvar - mu.pow (2 ) - logvar.exp()) BCE = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum' ) return KLD + BCE optimizer = optim.Adam(model.parameters(), lr=1e-3 ) data_loader = DataLoader(images, batch_size=16 , shuffle=True ) for epoch in range (30 ): total_losses = [] for batch in data_loader: batch = batch.to(device) optimizer.zero_grad() recon_batch, mu, logvar = model(batch) loss = loss_function(batch, recon_batch, mu, logvar) loss = loss / len (batch) total_losses.append(loss.item()) loss.backward() optimizer.step() print (f"Epoch {epoch+1 } , Loss: {np.mean(total_losses)} " )
此处对重构损失使用的是 BCELoss / 二进制交叉熵,这是因为 MNIST 数据集 为二值图像,只有0或1,所以对其进行重构只需要进行 BCELoss 即可.
VAE 变种 序列间自编码器 序列间的自编码器,其实就是 Sequence-to-Sequence Autoencoder ,也称为循环自动编码器。这部分内容在本站讲解序列到序列模型以及 Transformer 模型的文章中已经介绍。
预训练与微调 其他代价函数设计 待更:李宏毅深度学习笔记-无监督学习-深度自动编码器 - yueqiudian - 博客园
特征分离技术 待更:李宏毅深度学习笔记-无监督学习-深度自动编码器 - yueqiudian - 博客园
📃附录:变分推断 https://blog.csdn.net/m0_46385527/article/details/121149701 https://zhuanlan.zhihu.com/p/94638850 https://www.cnblogs.com/tshaaa/p/18651129 https://bluefisher.github.io/2020/02/06/理解-Variational-Lower-Bound/ https://blog.csdn.net/m0_46385527/article/details/121149701 https://www.cnblogs.com/song-lei/p/16210740.html
参考 Introduction to Autoencoders - PyImageSearch An introduction to AutoEncoder - 2201.03898.pdf (arxiv.org) 自动编码器(AutoEncoder)简介 - 知乎 李宏毅深度学习笔记-无监督学习-深度自动编码器 - yueqiudian - 博客园 稀疏自编码器-CSDN博客 [自编码器] [稀疏自编码器] Auto Encoder原理详解 - virter - 博客园 Introduction to autoencoders. - jeremyjordan.me Variational autoencoders. - jeremyjordan.me 从自编码器到变分自编码器(其二) | ATYUN.COM 官网 VAE论文原教旨解读(含公式推导和代码实现) - 知乎