整体框架 基本解、可行解、最优解、局部最优解
适应度函数
分类:
进化类算法(Evolutionary Algorithms) :由生物进化机制启发得到,包含交叉、变异、选择等操作,典型代表为遗传算法(Genetic Algorithm)和差分进化算法(Differential Evolution)。
群智能类算法(Swarm-based Algorithms) :通过使用单个生物个体作为搜索代理来模仿生物集群的集体行为,典型代表为蚁群算法(Ant Colony Optimization)、粒子群算法(Particle Swarm Optimization)和人工蜂群算法(Artificial Bee Colony Optimization)。
物理法则类算法(Physics-based Algorithms) :由物理法则启发得到,将客观规律转化为算法流程,典型代表为模拟退火算法(Simulated Annealing)和引力搜索算法(Gravitational Search Algorithm)。
其他类算法(Others) :由自然现象、数学原理、人造活动等启发得到,例如禁忌搜索(Tabu Search )、和声搜索(Harmony Search )、免疫算法(Immune Algorithm)。
遗传算法 遗传算法 (Genetic Algorithm,GA)在20世纪六七十年代由美国密歇根大学的 Holland教授 创立。是模拟达尔文生物进化论 的自然选择和遗传学机理的生物进化过程的计算模型。是一种通过模拟自然进化过程搜索最优解的方法。
原理与步骤 生物在其延续生存的过程中,逐渐适应其生存环境,使得其品质不断得到改良,这种生命现象称为进化 (Evolution)。生物的进化是以团体的形式共同进行的,这样的一个团体称为群体 (Population),组成群体的单个生物称为个体 (Individual),每个个体对其生存环境都有不同的适应能力,这种适应能力称为个体的适应度 (Fitness)。
此外,每个生物/个体还有的遗传和变异:
生物从其亲代继承特性或性状,这种生命现象就称为遗传 (Heredity)。控制生物遗传的物质单元称为基因 (Gene),它是有遗传效应的DNA片段。细胞在分裂时,遗传物质DNA通过复制 (Reproduction)而转移到新产生的细胞中,新细胞就继承了旧细胞的基因。
有性生物在繁殖下一代时,两个同源染色体之间遗过 交叉 (Crossover) 而重组。
在进行复制时,可能以很小的概率产生某些差错 ,从而使DNA发生某种变异 (Mutation),产生出新的染色体。
最终,按照达尔文的讲化论,那些具有较强适应环境变化能力的生物个体具有更高的生存能力容易存活下来,并有较多的机会产生后代;相反,具有较低生存能力的个体则被淘汰,或者产生后代的机会越来越少,直至消亡。即 自然选择,适者生存 。
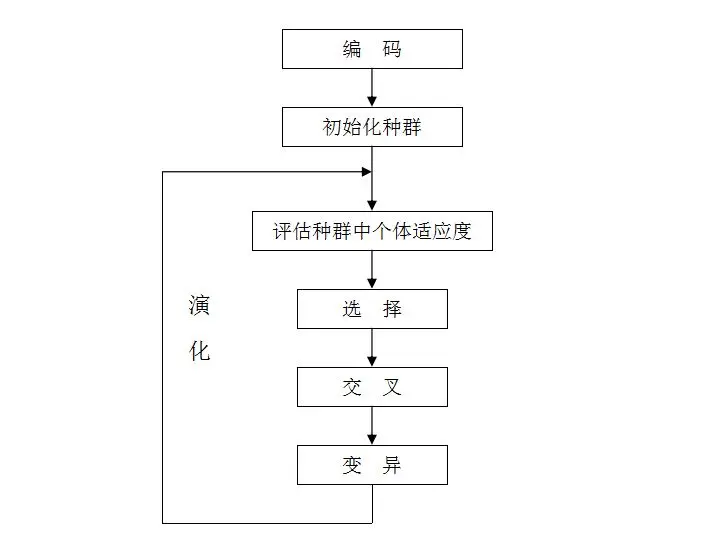
遗传算法的一般步骤 总结如下:
随机产生种群。 根据策略判断个体的适应度,是否符合优化准则,若符合,输出最佳个体及其最优解,结束。否则,进行下一步。 依据适应度选择父母,适应度高的个体被选中的概率高,适应度低的个体被淘汰。 用父母的染色体按照一定的方法进行交叉 ,生成子代。 对子代染色体进行变异 。 由交叉和变异产生新一代种群,返回步骤2,直到最优解产生。
编码、交叉与变异 编码方式 在遗传算法中,染色体是解空间中的解的表示形式。从问题的解到基因型的映射称为编码 ,即把一个问题的可行解从其解空间转换到遗传算法的搜索空间的转换方法 。
常见的编码方法有二进制编码 、格雷码编码 、 浮点数编码 、各参数级联编码 、多参数交叉编码 等。
二进制编码:即组成染色体的基因序列是由二进制数表示,具有编码解码简单易用,交叉变异易于程序实现等特点。
格雷编码:两个相邻的数用格雷码表示,其对应的码位只有一个不相同,从而可以提高算法的局部搜索能力。这是格雷码相比二进制码而言所具备的优势。
浮点数编码:是指将个体范围映射到对应浮点数区间范围,精度可以随浮点数区间大小而改变。
交叉策略 交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
变异策略 为了防止遗传算法在优化过程中陷入局部最优解,在搜索过程中,需要对个体进行变异。遗传算法中的个体变异运算是指个体染色体编码串中的某些基因座上的基因值用该基因座上的其余等位基因来替换,从而构成新的个体。基因位突变(Simple Mutation)、(非)均匀变异(Uniform Mutation)、边界变异(Boundary Mutation)和高斯近似变异等几种变异方法是针对二进制编码的个体基因突变的首选。
在实际应用中,主要采用单点变异,也叫位变异,即只需要对基因序列中某一个位进行变异,以二进制编码为例,即0变为1,而1变为0 。
轮盘赌选择 轮盘赌选择(Roulette Wheel Selection)、随机竞争选择(Stochastic Tournament)、最佳保留选择(Best Retention Selection)、无回放随机选择以及一些排序方式一般作为选择函数的选项。
完整代码模板 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 class Population : def __init__ (self,num,cross_p,mutation_p,max_gen ): self.num = num self.cp = cross_p self.mp = mutation_p self.gennum = max_gen self.oldsol = [] self.newsol = [] self.sp = [[] for i in range (self.num)] self.fitness = [[] for i in range (self.num)] self.init_sol() self.bestsol = self.oldsol[0 ] self.bestf = 0 pass def init_sol (self ): pass def compare (self ): for i in range (0 ,self.num): self.f[i] = func(self.oldsol[i])) f_sum = sum (self.f) for i in range (0 ,self.num): self.sp[i] = self.f[i]/f_sum def select (self ): point = 0 ; t = random.random() for p in self.sp: if p > t: break point += 1 if point >= self.num: point = 0 return point def cross (self,sol1,sol2 ): p = random.random() if sol1 != sol2 and p < self.cp: pass return sol1,sol2 def mutate (self,sol0 ): p = random.random() if p < self.mp: pass return sol0 def run (self ): self.compare() for i in range (0 ,self.num,2 ): sol1 = self.oldsol[self.select()] sol2 = self.oldsol[self.select()] sol1,sol2 = self.cross(sol1,sol2) sol1 = self.mutate(sol1) sol2 = self.mutate(sol2) self.newsol[i] = sol1 self.newsol[i+1 ] = sol2 flag = -1 for i in range (0 ,self.num): if self.bestf < self.f[i]: flag = i self.bestf = self.f[i] if flag >= 0 : self.bestsol = self.oldsol[flag] for i in range (0 ,self.num): self.oldsol[i] = self.newsol[i] def get_sol (self ): for i in range (0 ,self.gennum): self.run() return self.bestsol if __name__ == '__main__' : start=timeit.default_timer() pop = Population(2 ,0.8 ,0.1 ,200 ) ans = pop.get_sol() end=timeit.default_timer() print (ans) print ('运行时间: %s Seconds' %(end-start))
差分进化算法 差分进化算法(DE)简介及Python实现_de算法-CSDN博客
粒子群算法 1995年,受到鸟群觅食行为的规律性启发,James Kennedy 和 Russell Eberhart 建立了一个简化算法模型,经过多年改进最终形成了粒子群优化算法 (Particle Swarm Optimization, PSO)。
基本思想 设想这样一个场景:鸟群在森林中随机搜索食物,它们想要找到食物量最多的位置(全局最优解)。但是所有的鸟都不知道食物具体在哪个位置,只能感受 到食物大概在哪个方向 。记录 自己曾经找到过食物且量最多的位置,同时所有的鸟都共享 自己每一次发现食物的位置以及食物的量,这样鸟群就知道当前在哪个位置食物的量最多。
粒子抽象 粒子群算法通过设计一种无质量的粒子 来模拟鸟群中的鸟,粒子的位置可以延伸到N N N
粒子仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的方向。
规定第i i i X i = ( x i 1 , . . , x i D ) X_i=(x_{i1},..,x_{iD}) X i = ( x i 1 , .. , x i D ) V i V_i V i P i P_i P i f i f_i f i P g P_g P g f g = max i = 1 , . . , N f i f_g=\max\limits_{i=1,..,N}f_i f g = i = 1 , .. , N max f i N N N max \max max min \min min
值得注意的是,虽然遵循着鸟群的物理特性将V i V_i V i 位置增量 ,即下一步第i i i
X i ( k + 1 ) = X i ( k ) + V i ( k + 1 ) X^{(k+1)}_i=X^{(k)}_i+V^{(k+1)}_i X i ( k + 1 ) = X i ( k ) + V i ( k + 1 )
其中,速度的迭代公式被设计如下:
V i ( k + 1 ) = ω V i ( k ) + c 1 r 1 ( P i ( k ) − X i ( k ) ) + c 2 r 2 ( P g ( k ) − X i ( k ) ) V^{(k+1)}_i=\omega V^{(k)}_i+c_1r_1\left(P^{(k)}_i-X^{(k)}_i\right)+c_2r_2\left(P^{(k)}_g-X^{(k)}_i\right) V i ( k + 1 ) = ω V i ( k ) + c 1 r 1 ( P i ( k ) − X i ( k ) ) + c 2 r 2 ( P g ( k ) − X i ( k ) )
通常,我们把迭代更新的
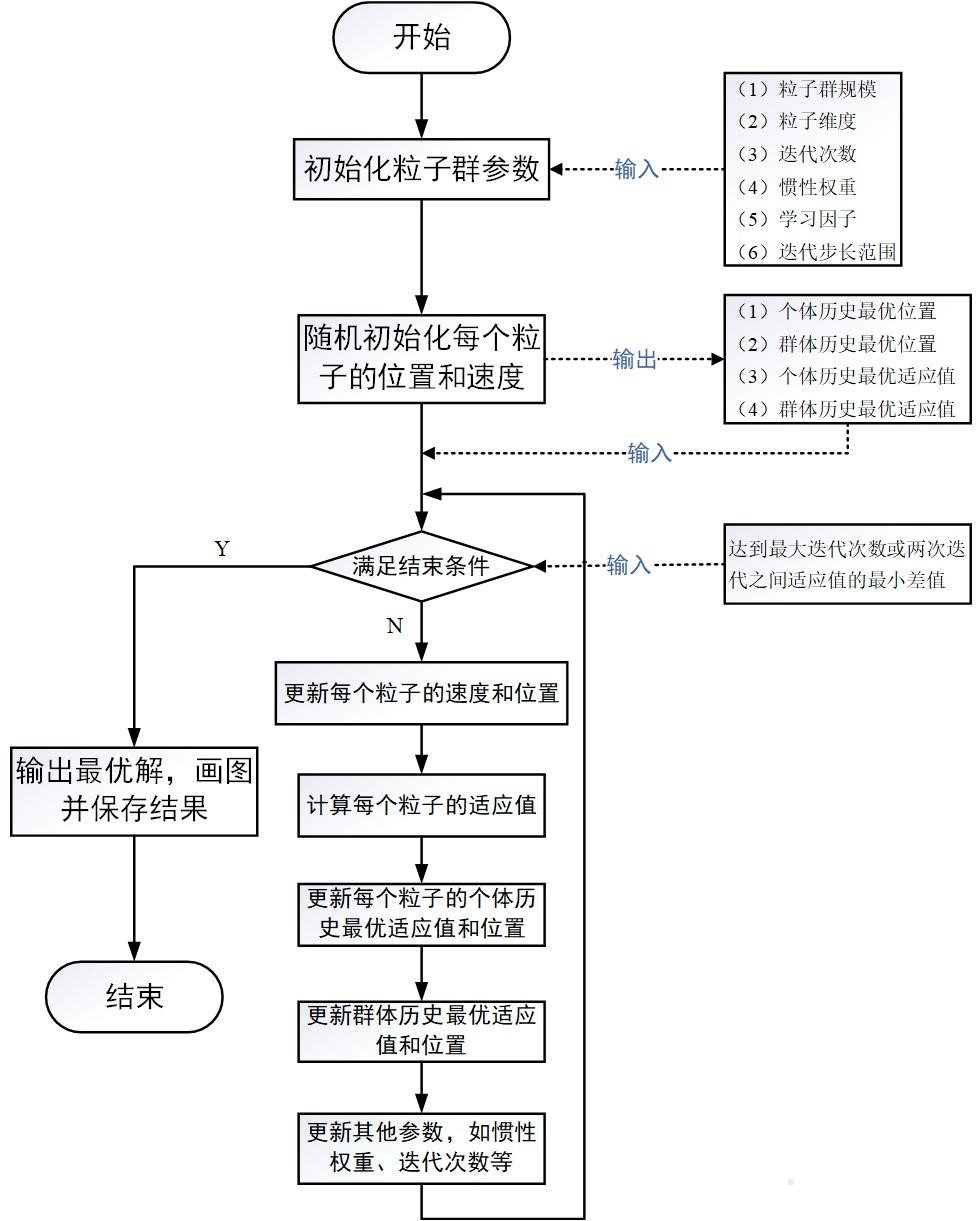
第一项称为惯性部分 ,ω \omega ω 0.9 0.9 0.9 0.4 0.4 0.4 第二项称为认知部分 、第三项称为社会部分 ,c 1 , c 2 c_1,c_2 c 1 , c 2 2.0 2.0 2.0 r 1 , r 2 r1,r2 r 1 , r 2 [ 0 , 1 ] [0,1] [ 0 , 1 ] 一般用户需要手动设置V max V_{\max} V m a x 最终,整个粒子群算法的流程如下图所示:
Python实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 import numpy as npimport randomimport matplotlib.pyplot as pltclass PSO (): def __init__ (self, pN, dim, max_iter ): self.w = 0.8 self.c1 = 2 self.c2 = 2 self.r1 = 0.6 self.r2 = 0.3 self.pN = pN self.dim = dim self.max_iter = max_iter self.X = np.zeros((self.pN, self.dim)) self.V = np.zeros((self.pN, self.dim)) self.pbest = np.zeros((self.pN, self.dim)) self.gbest = np.zeros((1 , self.dim)) self.p_fit = np.zeros(self.pN) self.fit = 1e10 def function (self, X ): return X**2 -4 *X+3 def init_Population (self ): for i in range (self.pN): for j in range (self.dim): self.X[i][j] = random.uniform(0 , 1 ) self.V[i][j] = random.uniform(0 , 1 ) self.pbest[i] = self.X[i] tmp = self.function(self.X[i]) self.p_fit[i] = tmp if tmp < self.fit: self.fit = tmp self.gbest = self.X[i] def iterator (self ): fitness = [] for t in range (self.max_iter): for i in range (self.pN): temp = self.function(self.X[i]) if temp < self.p_fit[i]: self.p_fit[i] = temp self.pbest[i] = self.X[i] if self.p_fit[i] < self.fit: self.gbest = self.X[i] self.fit = self.p_fit[i] for i in range (self.pN): self.V[i] = self.w * self.V[i] + self.c1 * self.r1 * (self.pbest[i] - self.X[i]) + \ self.c2 * self.r2 * (self.gbest - self.X[i]) self.X[i] = self.X[i] + self.V[i] fitness.append(self.fit) print (self.X[0 ], end=" " ) print (self.fit) return fitness my_pso = PSO(pN=30 , dim=1 , max_iter=100 ) my_pso.init_Population() fitness = my_pso.iterator() plt.figure(1 ) plt.title("Figure1" ) plt.xlabel("iterators" , size=14 ) plt.ylabel("fitness" , size=14 ) t = np.array([t for t in range (0 , 100 )]) fitness = np.array(fitness) plt.plot(t, fitness, color='b' , linewidth=3 ) plt.show()
蚁群算法 生物学家发现,自然界中的蚁群觅食是一种群体性行为,并非单只蚂蚁自行寻找食物源。蚂蚁在寻找食物源时,会在其经过的路径上释放一种信息素(Pheromone),并能够感知其它蚂蚁释放的信息素。信息素浓度的大小表征到食物源路径的远近,信息素浓度越高,表示对应的路径距离越短。
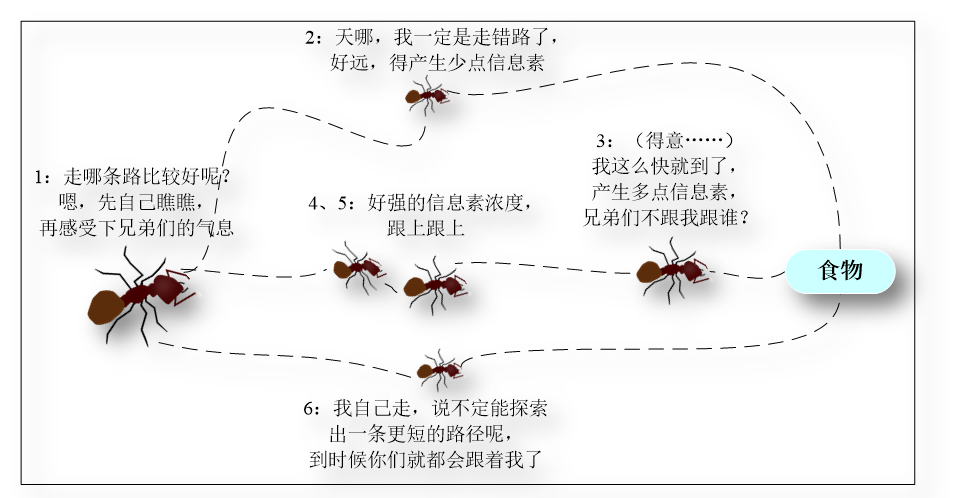
通常,蚂蚁会以较大的概率优先选择信息素浓度较高的路径,并释放一定量的信息素,以增强该条路径上的信息素浓度,这样会形成一个正反馈 。最终,蚂蚁能够找到一条从巢穴到食物源的最佳路径,即最短距离。值得一提的是,生物学家同时发现,路径上的信息素浓度会随着时间的推进而逐渐衰减。如下图所示:
20世纪90年代初,意大利学者 M.Dorigo 等人就是通过对这种群体智能行为的抽象建模,提出了蚁群优化算法 (Ant Colony Optimization, ACO ),为最优化问题、尤其是组合优化问题 的求解提供了一强有力的手段。
路径创建 M.Dorigo 等人最早将蚁群算法用于解决旅行商问题(Traveling Salesman Problem,TSP),并取得了较好的实验结果。为此,这里也以 TSP 为主要问题来对ACO的基本流程和数学模型进行阐述。
设整个蚂蚁群体中蚂蚁的数量为 m m m n n n d i j d_{ij} d ij t t t i i i j j j τ i j ( t ) \tau_{ij}(t) τ ij ( t ) τ i j ( 0 ) = τ 0 , ∀ i , j = 1 , . . , n \tau_{ij}(0)=\tau_0,\;\forall i,j=1,..,n τ ij ( 0 ) = τ 0 , ∀ i , j = 1 , .. , n
设P i j ( k ) ( t ) P_{ij}^{(k)}(t) P ij ( k ) ( t ) t t t k ( k = 1 , . . , m ) k\quad(k=1,..,m) k ( k = 1 , .. , m ) i i i j j j 转移概率 ,定义:
P i j ( k ) ( t ) = { [ τ i j ( t ) ] α × [ η i j ( t ) ] β ∑ s ∈ a l l o w e d k [ τ i s ( t ) ] α × [ η i s ( t ) ] β if j ∈ a l l o w e d k 0 otherwise P_{ij}^{(k)}(t)=\begin{cases} \begin{aligned}&\frac{[\tau_{ij}(t)]^\alpha\times[\eta_{ij}(t)]^\beta}{\sum\limits_{s\in allowed_k}[\tau_{is}(t)]^\alpha\times[\eta_{is}(t)]^\beta}&\text{if }j\in allowed_k\\ &0&\text{otherwise}\end{aligned} \end{cases} P ij ( k ) ( t ) = ⎩ ⎨ ⎧ s ∈ a ll o w e d k ∑ [ τ i s ( t ) ] α × [ η i s ( t ) ] β [ τ ij ( t ) ] α × [ η ij ( t ) ] β 0 if j ∈ a ll o w e d k otherwise
其中,
η i j ( t ) = 1 / d i j \eta_{ij}(t)=1/d_{ij} η ij ( t ) = 1/ d ij 期望 程度;a l l o w e d k allowed_k a ll o w e d k k k k a l l o w e d k allowed_k a ll o w e d k ( n − 1 ) (n-1) ( n − 1 ) k k k a l l o w e d k allowed_k a ll o w e d k α \alpha α β \beta β 当α = 0 \alpha=0 α = 0 贪心算法 ,最邻近城市被选中的概率最大。β = 0 \beta=0 β = 0 正反馈 的启发式算法,蚂蚁完全只根据信息素浓度确定路径,算法将快速收敛 ,这样构建出的最优路径往往与实际目标有着较大的差异,算法的性能比较糟糕。
最终经过n n n 一次迭代 ,每只蚂蚁所走过的路径就是一个解。
信息素挥发 由于蚂蚁释放信息素的同时,各个城市间连接路径上的信息素逐渐消失,设参数ρ ∈ ( 0 , 1 ) \rho\in(0,1) ρ ∈ ( 0 , 1 ) 挥发程度 。则当所有蚂蚁完成一次循环后,各个城市间连接路径上的信息素浓度需进行实时更新,即:
τ i j ( t + 1 ) = ( 1 − ρ ) ⋅ τ i j ( t ) + Δ τ i j Δ τ i j = ∑ k = 1 m Δ τ i j ( k ) \begin{aligned} \tau_{ij}(t + 1) &= (1 - \rho ) \cdot \tau_{ij}(t) + \Delta \tau_{ij}\\ \Delta \tau_{ij} &= \sum_{k = 1}^{m}\Delta \tau_{ij}^{(k)} \end{aligned} τ ij ( t + 1 ) Δ τ ij = ( 1 − ρ ) ⋅ τ ij ( t ) + Δ τ ij = k = 1 ∑ m Δ τ ij ( k )
其中,Δ τ i j ( k ) \Delta\tau_{ij}^{(k)} Δ τ ij ( k ) k k k i i i j j j Δ τ i j \Delta\tau_{ij} Δ τ ij i i i j j j
而针对Δ τ i j ( k ) \Delta\tau_{ij}^{(k)} Δ τ ij ( k )
Ant Cycle System模型利用蚂蚁经过路径的整体信息(经过路径的总长)计算释放的信息素浓度; Ant Quantity System模型利用蚂蚁经过路径的局部信息(经过各个城市间的距离)计算释放的信息素浓度; Ant Density System模型更为简单地将信息素释放的浓度取为恒值,并没有考虑不同蚂蚁经过路径长度的影响。 通常,选用Ant Cycle System计算释放的信息素浓度,即蚂蚁经过的路径越短,释放的信息素浓度越高。其公式为:
Δ τ i j ( k ) ( t ) = { 1 C k if the k -th ant traverses ( i , j ) 0 otherwise \Delta\tau_{ij}^{(k)}(t)=\left\{\begin{aligned} &\frac{1}{C_k}&\text{if the $k$-th ant traverses }(i, j)\\ &0&\text{otherwise} \end{aligned}\right. Δ τ ij ( k ) ( t ) = ⎩ ⎨ ⎧ C k 1 0 if the k -th ant traverses ( i , j ) otherwise
其中,C k C_k C k k k k 总路径长度 。相当于每只蚂蚁将1 1 1 Q Q Q Q Q Q
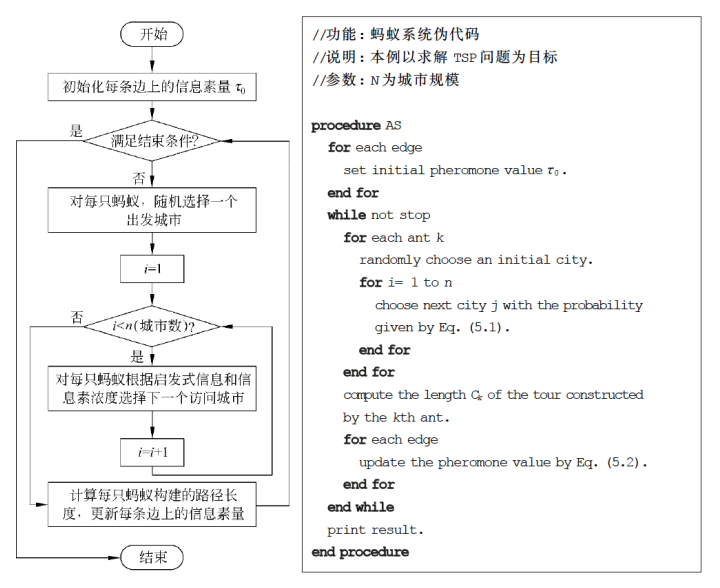
算法流程
Note: 在选择下一个访问的城市时,与遗传算法一样,同样根据轮盘赌的方法选择
人工蜂群算法 人工蜂群算法(Artificial Bee Colony,ABC ) 是由土耳其学者Karaboga 于 2005 年提出的一种新颖的基于群智能的全局优化算法,其直观背景来源于蜂群的采蜜行为,蜜蜂根据各自的分工进行不同的活动,并实现蜂群信息的共享和交流,从而找到问题的最优解。
生物背景 蜜蜂是一种群居昆虫,自然界中的蜜蜂总能在任何环境下以极高的效率找到优质蜜源,且能适应环境的改变。蜜蜂群的采蜜系统主要由蜜源、采蜜蜂、跟随蜂、侦查蜂等组成(某些资料有雇佣蜂、非雇佣蜂之分):
蜜源:蜜源的位置(假设有D D D S N SN SN 可行解 ,是人工蜂群算法中所要处理的基本对象。蜜源的优劣用实际问题的适应度(目标函数)来评价。 采蜜蜂:采蜜蜂(假设有S N SN SN 贪婪准则 ,比较记忆中的最优解和邻域搜索解,当搜索解优于记忆最优解时,替换记忆解;反之,保持不变。在所有的采蜜蜂完成邻域搜索后,采蜜蜂回蜂房跳摆尾舞与跟随蜂共享蜜源信息 。 跟随蜂:跟随峰的数量与采蜜蜂相同(假设有S N SN SN 贪婪准则 ,比较跟随蜂搜索解与原采蜜蜂的解,当搜索解优于原采蜜蜂的解时,替换原采蜜蜂的解,完成角色互换;反之,保持不变。 侦查蜂:若某处蜜源陷入局部最优,采用侦查蜂大步长搜索 的方式探索最优解。 基本原理 蜂群初始化 根据第j ( j = 1 , 2 , . . , D ) j\;(j=1,2,..,D) j ( j = 1 , 2 , .. , D ) x max , j x_{\max,j} x m a x , j x min , j x_{\min,j} x m i n , j 随机 生成S N SN SN i i i X i = { x i 1 , x i 2 , . . , x i D } X_i=\{x_{i1},x_{i2},..,x_{iD}\} X i = { x i 1 , x i 2 , .. , x i D }
x i j = x min , j + rand [ 0 , 1 ] ( x max , j − x max , j ) , i = 1 , 2 , . . , S N x_{ij}=x_{\min,j}+\text{rand}[0,1](x_{\max,j}-x_{\max,j}),\quad i=1,2,..,SN x ij = x m i n , j + rand [ 0 , 1 ] ( x m a x , j − x m a x , j ) , i = 1 , 2 , .. , SN
rand [ 0 , 1 ] \text{rand}[0,1] rand [ 0 , 1 ] [ 0 , 1 ] [0,1] [ 0 , 1 ]
采蜜蜂阶段 开始搜索时,第i i i i i i 随机 选取第k , k ≠ i k,\;k\neq i k , k = i V i = { v i 1 , v i 2 , . . , v i D } V_i=\{v_{i1},v_{i2},..,v_{iD}\} V i = { v i 1 , v i 2 , .. , v i D }
v i j = x i j + ϕ i j ( x i j − x k j ) , j = 1 , 2 , . . , D v_{ij}=x_{ij}+\phi_{ij}(x_{ij}-x_{kj}),\quad j=1,2,..,D v ij = x ij + ϕ ij ( x ij − x kj ) , j = 1 , 2 , .. , D
ϕ i j \phi_{ij} ϕ ij [ − 1 , 1 ] [-1,1] [ − 1 , 1 ]
比较V i V_i V i X i X_i X i X i X_i X i
跟随蜂阶段 跟随峰阶段,采蜜蜂在舞蹈区分享蜜源信息。跟随蜂分析这些信息,采用轮盘赌策略 来选择蜜源跟踪开采,以保证适应值更高的蜜源开采的概率更大。
p i = fit i ∑ i = j S N fit j p_i=\frac{\text{fit}_i}{\sum_{i=j}^{SN}\text{fit}_j} p i = ∑ i = j SN fit j fit i
跟随蜂开采过程与雇佣蜂一样,生成新蜜源并留下更优适应度的蜜源。
蜜源拥有参数trial \text{trial} trial trial = 0 \text{trial}=0 trial = 0 trial ← trial + 1 \text{trial}\leftarrow\text{trial}+1 trial ← trial + 1 trial \text{trial} trial limit \text{limit} limit
侦查蜂阶段 侦查蜂阶段,第i i i
x i j = x min , j + rand [ 0 , 1 ] ( x max , j − x max , j ) , i = 1 , 2 , . . , S N x_{ij}=x_{\min,j}+\text{rand}[0,1](x_{\max,j}-x_{\max,j}),\quad i=1,2,..,SN x ij = x m i n , j + rand [ 0 , 1 ] ( x m a x , j − x m a x , j ) , i = 1 , 2 , .. , SN
Python实现 整个算法流程就是上述三个阶段的不断迭代 。下面以计算函数
y = 1 4000 ∑ i = 1 n x i 2 − ∏ i = 1 n cos ( x i i ) + 1 y=\frac1{4000}\sum_{i=1}^nx_i^2-\prod_{i=1}^n\cos\left(\frac{x_i}{\sqrt i}\right)+1 y = 4000 1 i = 1 ∑ n x i 2 − i = 1 ∏ n cos ( i x i ) + 1
的最小值为例,进行人工蜂群算法的优化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 import numpy as npimport random, math, copyimport matplotlib.pyplot as plt def GrieFunc (data ): s1 = 0. s2 = 1. for k, x in enumerate (data): s1 = s1 + x ** 2 s2 = s2 * math.cos(x / math.sqrt(k+1 )) y = (1. / 4000. ) * s1 - s2 + 1 return 1. / (1. + y) class ABSIndividual : def __init__ (self, bound ): self.score = 0. self.invalidCount = 0 self.chrom = [random.uniform(a,b) for a,b in zip (bound[0 ,:],bound[1 ,:])] self.calculateFitness() def calculateFitness (self ): self.score = GrieFunc(self.chrom) class ArtificialBeeSwarm : def __init__ (self, foodCount, onlookerCount, bound, maxIterCount=1000 , maxInvalidCount=200 ): self.foodCount = foodCount self.onlookerCount = onlookerCount self.bound = bound self.maxIterCount = maxIterCount self.maxInvalidCount = maxInvalidCount self.foodList = [ABSIndividual(self.bound) for k in range (self.foodCount)] self.foodScore = [d.score for d in self.foodList] self.bestFood = self.foodList[np.argmax(self.foodScore)] def updateFood (self, i ): k = random.randint(0 , self.bound.shape[1 ] - 1 ) j = random.choice([d for d in range (self.bound.shape[1 ]) if d !=i]) vi = copy.deepcopy(self.foodList[i]) vi.chrom[k] += random.uniform(-1.0 , 1.0 ) * (vi.chrom[k] - self.foodList[j].chrom[k]) vi.chrom[k] = np.clip(vi.chrom[k], self.bound[0 , k], self.bound[1 , k]) vi.calculateFitness() if vi.score > self.foodList[i].score: self.foodList[i] = vi if vi.score > self.foodScore[i]: self.foodScore[i] = vi.score if vi.score > self.bestFood.score: self.bestFood = vi self.foodList[i].invalidCount = 0 else : self.foodList[i].invalidCount += 1 def employedBeePhase (self ): for i in xrange(0 , self.foodCount): self.updateFood(i) def onlookerBeePhase (self ): foodScore = [d.score for d in self.foodList] maxScore = np.max (foodScore) accuFitness = [(0.9 *d/maxScore+0.1 , k) for k,d in enumerate (foodScore)] for k in xrange(0 , self.onlookerCount): i = random.choice([d[1 ] for d in accuFitness if d[0 ] >= random.random()]) self.updateFood(i) def scoutBeePhase (self ): for i in xrange(0 , self.foodCount): if self.foodList[i].invalidCount > self.maxInvalidCount: self.foodList[i] = ABSIndividual(self.bound) self.foodScore[i] = max (self.foodScore[i], self.foodList[i].score) def solve (self ): trace = [] trace.append((self.bestFood.score, np.mean(self.foodScore))) for k in range (self.maxIterCount): self.employedBeePhase() self.onlookerBeePhase() self.scoutBeePhase() trace.append((self.bestFood.score, np.mean(self.foodScore))) print (self.bestFood.score) self.printResult(np.array(trace)) def printResult (self, trace ): x = np.arange(0 , trace.shape[0 ]) plt.plot(x, [(1 -d)/d for d in trace[:, 0 ]], 'r' , label='optimal value' ) plt.plot(x, [(1 -d)/d for d in trace[:, 1 ]], 'g' , label='average value' ) plt.xlabel("Iteration" ) plt.ylabel("function value" ) plt.title("Artificial Bee Swarm algorithm for function optimization" ) plt.legend() plt.show() if __name__ == "__main__" : random.seed() vardim = 25 bound = np.tile([[-600 ], [600 ]], vardim) abs = ArtificialBeeSwarm(30 , 30 , bound, 1000 , 200 ) abs .solve()
灰狼优化算法 灰狼优化(Grey Wolf Optimization, GWO)算法于 2014 年由 Mirjalili 等人提出的一种基于群体智能的随机优化算法 ,该算法源于灰狼群中严格的社会层级制度和社会行为。通过模拟灰狼群体的寻食过程,实现对复杂优化问题的求解。通过灵活地调整群体中每只“狼”的位置和行为,以最小化或最大化给定问题的目标函数。
自然界的灰狼 自然界中灰狼常以群体的形式出没,每个群体的灰狼个数在5 ∼ 12 5\sim12 5 ∼ 12 金字塔的结构 。其中,α α α β β β α α α α α α α α α β β β α α α δ δ δ α α α β β β ω ω ω
如果在寻优过程中,α α α β β β 适应度值 (对应的目标函数值)较低,那么它们有几率会降为δ δ δ ω ω ω
狩猎/寻优过程 在狩猎过程中,灰狼会采用跟踪包围 的策略来追捕猎物。而这个行为正是 GWO 算法的核心思想。该行为可以用下式表示:
D = ∣ C ⊙ X p ( t ) − X ( t ) ∣ X ( t + 1 ) = X p ( t ) − A ⊙ D \begin{aligned} D&=\vert C\odot X_p^{(t)}-X^{(t)}\vert\\ X^{(t+1)}&=X_p^{(t)}-A\odot D \end{aligned} D X ( t + 1 ) = ∣ C ⊙ X p ( t ) − X ( t ) ∣ = X p ( t ) − A ⊙ D
其中,上标( t ) , ( t + 1 ) (t),\;(t+1) ( t ) , ( t + 1 ) t , t + 1 t,\;t+1 t , t + 1 X p X_p X p X X X A , D A,\;D A , D a a a [ 0 , 1 ] [0,1] [ 0 , 1 ] r 1 , r 2 r_1,\;r_2 r 1 , r 2
A = 2 a ⊙ r 1 − a C = 2 r 2 a = 2 − 2 t t max \begin{aligned} A&=2a\odot r_1-a\\ C&=2r_2\\ a&=2-\frac{2t}{t_{\max}} \end{aligned} A C a = 2 a ⊙ r 1 − a = 2 r 2 = 2 − t m a x 2 t
其中,a a a 2 2 2 线性减小 到0 0 0
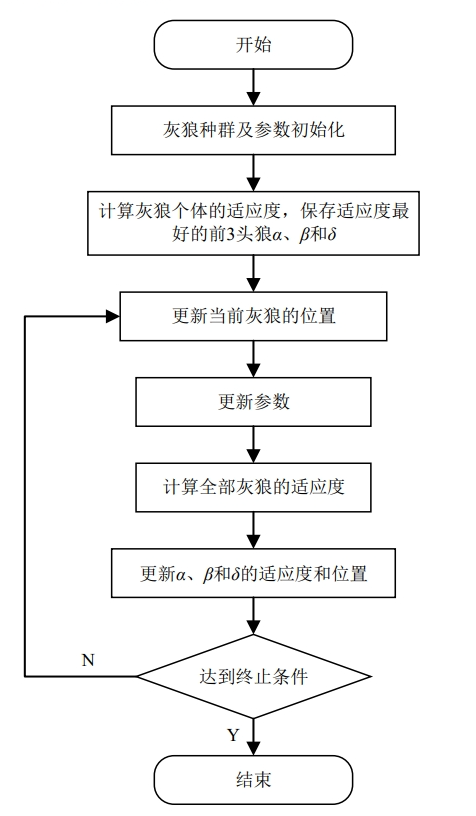
GWO算法正是利用这个数学模型。在每次迭代过程中,保留当前种群中的最好三只灰狼( α , β , δ \alpha,\beta,\delta α , β , δ ω ω ω α , β , δ \alpha,\beta,\delta α , β , δ
上述行为的数学表达如下:
D α = ∣ C 1 ⊙ X α ( t ) − X ( t ) ∣ D β = ∣ C 2 ⊙ X β ( t ) − X ( t ) ∣ D δ = ∣ C 3 ⊙ X δ ( t ) − X ( t ) ∣ \begin{aligned} D_{\alpha}&=\vert C_1\odot X_{\alpha}^{(t)}-X^{(t)}\vert\\ D_{\beta}&=\vert C_2\odot X_{\beta}^{(t)}-X^{(t)}\vert\\ D_{\delta}&=\vert C_3\odot X_{\delta}^{(t)}-X^{(t)}\vert\\ \end{aligned} D α D β D δ = ∣ C 1 ⊙ X α ( t ) − X ( t ) ∣ = ∣ C 2 ⊙ X β ( t ) − X ( t ) ∣ = ∣ C 3 ⊙ X δ ( t ) − X ( t ) ∣
X 1 ( t + 1 ) = X α ( t ) − A 1 ⊙ D α X 2 ( t + 1 ) = X β ( t ) − A 2 ⊙ D β X 3 ( t + 1 ) = X δ ( t ) − A 3 ⊙ D δ X ( t + 1 ) = 1 3 ( X 1 ( t + 1 ) + X 2 ( t + 1 ) + X 3 ( t + 1 ) ) \begin{aligned} X_1^{(t+1)}&=X^{(t)}_{\alpha}-A_1\odot D_{\alpha}\\ X_2^{(t+1)}&=X^{(t)}_{\beta}-A_2\odot D_{\beta}\\ X_3^{(t+1)}&=X^{(t)}_{\delta}-A_3\odot D_{\delta}\\\\ X^{(t+1)}&=\frac13\left(X_1^{(t+1)}+X_2^{(t+1)}+X_3^{(t+1)}\right) \end{aligned} X 1 ( t + 1 ) X 2 ( t + 1 ) X 3 ( t + 1 ) X ( t + 1 ) = X α ( t ) − A 1 ⊙ D α = X β ( t ) − A 2 ⊙ D β = X δ ( t ) − A 3 ⊙ D δ = 3 1 ( X 1 ( t + 1 ) + X 2 ( t + 1 ) + X 3 ( t + 1 ) )
整个算法流程如下图所示:
收敛性分析 直观简单的收敛性分析:见优化算法笔记(十八)灰狼算法 - 简书
Python实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 import randomimport numpydef GWO (objf, lb, ub, dim, SearchAgents_no, Max_iter ): '''objf: 目标函数; lb, ub: 上下限; dim: 维度; SerchAgents_no: 搜索代理/狼的个数; Max_iter: 最大迭代数; ''' Alpha_pos = numpy.zeros(dim) Alpha_score = float ("inf" ) Beta_pos = numpy.zeros(dim) Beta_score = float ("inf" ) Delta_pos = numpy.zeros(dim) Delta_score = float ("inf" ) if not isinstance (lb, list ): lb = [lb] * dim if not isinstance (ub, list ): ub = [ub] * dim Positions = numpy.zeros((SearchAgents_no, dim)) for i in range (dim): Positions[:, i] = numpy.random.uniform(0 , 1 , SearchAgents_no) * (ub[i] - lb[i]) + lb[i] Convergence_curve = numpy.zeros(Max_iter) for l in range (0 , Max_iter): for i in range (0 , SearchAgents_no): for j in range (dim): Positions[i, j] = numpy.clip(Positions[i, j], lb[j], ub[ j]) fitness = objf(Positions[i, :]) if fitness < Alpha_score: Alpha_score = fitness Alpha_pos = Positions[i, :].copy() if (fitness > Alpha_score and fitness < Beta_score): Beta_score = fitness Beta_pos = Positions[i, :].copy() if (fitness > Alpha_score and fitness > Beta_score and fitness < Delta_score): Delta_score = fitness Delta_pos = Positions[i, :].copy() a = 2 - l * ((2 ) / Max_iter); for i in range (0 , SearchAgents_no): for j in range (0 , dim): r1 = random.random() r2 = random.random() A1 = 2 * a * r1 - a; C1 = 2 * r2; D_alpha = abs (C1 * Alpha_pos[j] - Positions[ i, j]); X1 = Alpha_pos[j] - A1 * D_alpha; r1 = random.random() r2 = random.random() A2 = 2 * a * r1 - a; C2 = 2 * r2; D_beta = abs (C2 * Beta_pos[j] - Positions[i, j]); X2 = Beta_pos[j] - A2 * D_beta; r1 = random.random() r2 = random.random() A3 = 2 * a * r1 - a; C3 = 2 * r2; D_delta = abs (C3 * Delta_pos[j] - Positions[i, j]); X3 = Delta_pos[j] - A3 * D_delta; Positions[i, j] = (X1 + X2 + X3) / 3 Convergence_curve[l] = Alpha_score; if (l % 1 == 0 ): print (['迭代次数为' + str (l) + ' 的迭代结果' + str (Alpha_score)]); ''' 下面用于测试 ''' def F1 (x ): s=numpy.sum (x**2 ); return s Max_iter = 1000 lb = -100 ub = 100 dim = 30 SearchAgents_no = 5 x = GWO(F1, lb, ub, dim, SearchAgents_no, Max_iter)
参考资料 全文六万字《计算智能》智能优化算法 张军【Python】-CSDN博客 遗传算法入门详解 - 知乎 遗传算法GA原理详解及实例应用 附Python代码_应用实例遗传算法-CSDN博客 用Python实现遗传算法 - 知乎 差分进化算法(DE)简介及Python实现_de算法-CSDN博客 Python粒子群优化算法实现PSO -CSDN博客 【优秀作业】蚁群优化算法 (qq.com) 蚁群优化算法(Ant Colony Optimization, ACO) - 知乎 优化算法——人工蜂群算法(ABC)(转发) - 知乎 人工蜂群算法代码实现 python_人工蜂群算法python代码-CSDN博客 【优化算法】简述灰狼优化算法(GWO)原理_灰狼算法-CSDN博客