Intro

清晨的咖啡杯中，奶精与黑咖啡的交融是一场微观世界的扩散（Diffusion）。无序的布朗运动将奶滴打散，直至达成均匀的混沌——这是热力学第二定律的具象化：熵增不可逆。 但是如果有一种像电影《信条（TENET）》那样的时间钳形装置，我们或许就能看到奶精和咖啡重新分离回归原位的奇观，熵减了！

破坏一样东西总比创造它容易得多，但是我们是否可以构建一种模型，这个模型能够学习到如何将数据一步步破坏，然后反过来通过反变换将它一步步从被破坏后的样子还原回来呢？这种模型正是一种生成式模型的新思路， Diffusion Models 就是该思想的贡献者之一，始于2020年所提出的DDPM（Denoising Diffusion Probabilistic Model）。

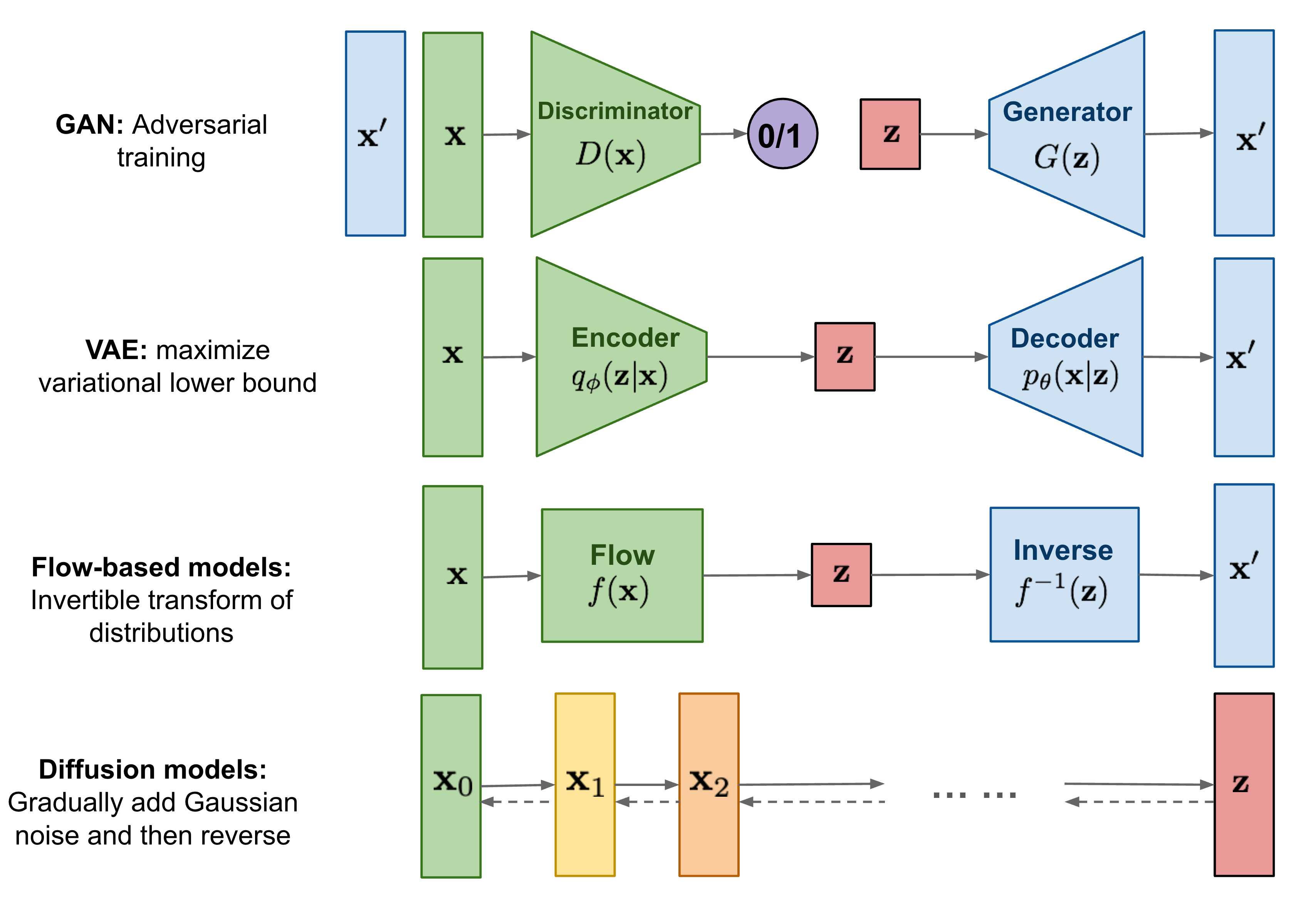
和我们之前介绍的 VAE、GAN 不同，Diffusion models 将原始输入样本x0\mathbf x_0 逐步地增加高斯噪声（称为前向扩散过程），最终得到z\bf z，然后再逐步进行反变换还原（称为反向扩散过程）。模型训练完毕后只需执行后半段的反变换过程，即可实现生成需求。

原理推导 (DDPM)

前向扩散

对于服从真实分布的样本x0∼q(x)\mathbf x_0\sim q(\mathbf x)，前向扩散过程（forward diffusion process）被定义为将x0\mathbf x_0 逐步增加TT 步高斯噪声的，得到一串x1,…,xT\mathbf{x}_1, \dots, \mathbf{x}_T 噪声序列，由一系列方差{βt∈(0,1)}t=1T\{\beta_t \in (0, 1)\}_{t=1}^T 来调度。并且遵从马尔可夫链规则，有：

q(xt∣xt−1)=N(xt;1−βtxt−1,βtI),q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) = \mathcal{N}(\mathbf{x}_t; \sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I}), \quad q(\mathbf{x}_{1:T} \vert \mathbf{x}_0) = \prod^T_{t=1} q(\mathbf{x}_t \vert \mathbf{x}_{t-1})

当T→∞T\to\infty 时，xT\mathbf x_T 服从于各向同性的多元高斯分布（isotropic Gaussian distribution，也叫球形高斯分布），即各个方向（每一维度）的方差都相等（Σ=σI\Sigma=\sigma\bf I）。

上面这个公式给出了已知xt−1\mathbf x_{t-1} 后通过增加高斯噪声得到xt\mathbf x_t 的分布，其实表面上看起来有点吓人，但是我们可以稍微推导一下：

xt∼N(1−βtxt−1,βtI)xt−1−βtxt−1∼N(0,βtI)(xt−1−βtxt−1)/βt∼N(0,I)\begin{aligned} \mathbf x_t&\sim \mathcal{N}(\sqrt{1 - \beta_t} \mathbf{x}_{t-1}, \beta_t\mathbf{I})\\ \mathbf x_t-\sqrt{1 - \beta_t} \mathbf{x}_{t-1} &\sim \mathcal{N}(0, \beta_t\mathbf{I})\\ \big(\mathbf x_t-\sqrt{1 - \beta_t} \mathbf{x}_{t-1}\big)/\sqrt{\beta_t} &\sim \mathcal{N}(0, \mathbf{I}) \end{aligned}

令ϵt−1∼N(0,I)\mathbf\epsilon_{t-1}\sim\mathcal N(0,\mathbf I)，我们就可以显式地写出如何将xt\mathbf x_t 拆分成xt−1\mathbf x_{t-1} 和高斯噪声ϵt−1\mathbf\epsilon_{t-1} 的加和：

xt=1−βtxt−1+βtϵt−1\mathbf x_t=\sqrt{1 - \beta_t} \mathbf{x}_{t-1}+\sqrt{\beta_t}\boldsymbol{\epsilon}_{t-1}

这个显式的递推公式还可以指导我们直接一步到位推导出xt\mathbf x_t 和xt−2\mathbf x_{t-2} 的关系（在原论文中，作者还令αt=1−βt\alpha_t=1-\beta_t 便于后续推导）：

xt=1−βtxt−1+βtϵ1=αtxt−1+1−αtϵ1=αt(αt−1xt−2+1−αt−1ϵ2)+1−αtϵ1=αtα1x2+αt1−αt−1ϵ2+1−αtϵ1=αtα1x2+1−αtα1ϵˉ2where ϵˉ2∼N(0,I)∗Tips  N(0,σ12I)+N(0,σ22I)=N(0,(σ12+σ22)I)\begin{aligned} \mathbf x_t&=\sqrt{1 - \beta_t} \mathbf{x}_{t-1}+\sqrt{\beta_t}\boldsymbol{\epsilon}_{1}\\ &=\sqrt{\alpha_t}\mathbf{x}_{t-1}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{1}\\ &=\sqrt{\alpha_t}\big(\sqrt{\alpha_{t-1}}\mathbf x_{t-2}+\sqrt{1-\alpha_{t-1}}\boldsymbol{\epsilon}_{2}\big)+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{1}\\ &=\sqrt{\alpha_t\alpha_{1}}\mathbf x_{2}+\sqrt{\alpha_t}\sqrt{1-\alpha_{t-1}}\boldsymbol{\epsilon}_{2}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{1}\\ &=\sqrt{\alpha_t\alpha_{1}}\mathbf x_{2}+\sqrt{1-\alpha_t\alpha_{1}}\bar{\boldsymbol{\epsilon}}_{2} \quad\text{where }\bar{\boldsymbol{\epsilon}}_{2}\sim\mathcal{N}(0,\mathbf I) \\\\ &^{*\text{Tips}}\;\mathcal{N}(0,\sigma_1^2\mathbf I)+\mathcal{N}(0,\sigma_2^2\mathbf I)=\mathcal{N}\big(0,(\sigma_1^2+\sigma_2^2)\mathbf I\big) \end{aligned}

更进一步地，令αˉt=∏i=1tαi\bar{\alpha}_t = \prod_{i=1}^t \alpha_i ，可以得到xt\mathbf x_t 和x0\mathbf x_{0} 的关系（★）：

xt=αˉtx0+1−αˉtϵt(⋆)i.e.  q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)\begin{aligned} \mathbf{x}_t &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t \quad(\star)\\ i.e.\;q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}

反过来，有：

x0=1αˉt  xt−1αˉt−1  ϵt(⋆)\mathbf{x}_0=\sqrt{\frac1{\bar{\alpha}_t}}\;\mathbf{x}_t-\sqrt{\frac1{\bar{\alpha}_t}-1}\;\boldsymbol{\epsilon}_t\quad(\star)

通常，当样本被加噪变得更嘈杂时，其可以负担得起更大的更新步骤，所以有β1<β2<⋯<βT\beta_1 < \beta_2 < \dots < \beta_T ，对应有αˉ1>⋯>αˉT\bar{\alpha}_1 > \dots > \bar{\alpha}_T.

反向扩散

一个很直观的想法就是，既然xt\mathbf x_{t} 可以通过公式αtxt−1+1−αtϵ1\sqrt{\alpha_t}\mathbf{x}_{t-1}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{1} 得到，那么反过来我们可以显式地写出xt−1\mathbf x_{t-1} 的公式：

xt−1=xt−1−αtϵ1αt\mathbf x_{t-1}=\frac{\mathbf x_{t}-\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{1}}{\sqrt{\alpha_{t}}}

所以如果我们需要学习一个从xt\mathbf x_{t} 到xt−1\mathbf x_{t-1} 的函数μθ(xt,t)\boldsymbol\mu_\theta(\mathbf x_{t},t)，关键就是能够建模噪声ϵt−1\boldsymbol{\epsilon}_{t-1}（只有它是非定值）. 按照朴素思想，如果我们可以设计MSE Loss来优化参数：

∥xt−1−μθ(xt,t)∥2\Vert\mathbf x_{t-1}-\boldsymbol\mu_\theta(\mathbf x_{t},t)\Vert^2

其实它就等价于优化：

∥ϵ1−ϵθ(xt,t)∥2\Vert\boldsymbol\epsilon_{1}-\boldsymbol\epsilon_\theta(\mathbf x_{t},t)\Vert^2

更进一步地，在训练模型时x0\mathbf x_0 是训练集中已知的输入，我们可以将 (★) 式建立的x0\mathbf x_0 和xt\mathbf x_t 的关系式代换上去，然后直接训练模型即可。但在实践中，这种方法可能有方差过大的风险（每个时间步tt 都要重新采样），从而导致收敛过慢等问题。对此可以用一种积分技巧将多次采用的ϵt\boldsymbol{\epsilon}_t 采用统一的ϵ\boldsymbol{\epsilon} 代替，最终的结果与DDPM 原论文所给的损失一致。这种策略具体可参见苏剑林老师在其博客中的详细描述。接下来本文会讲一讲原论文的推导视角。

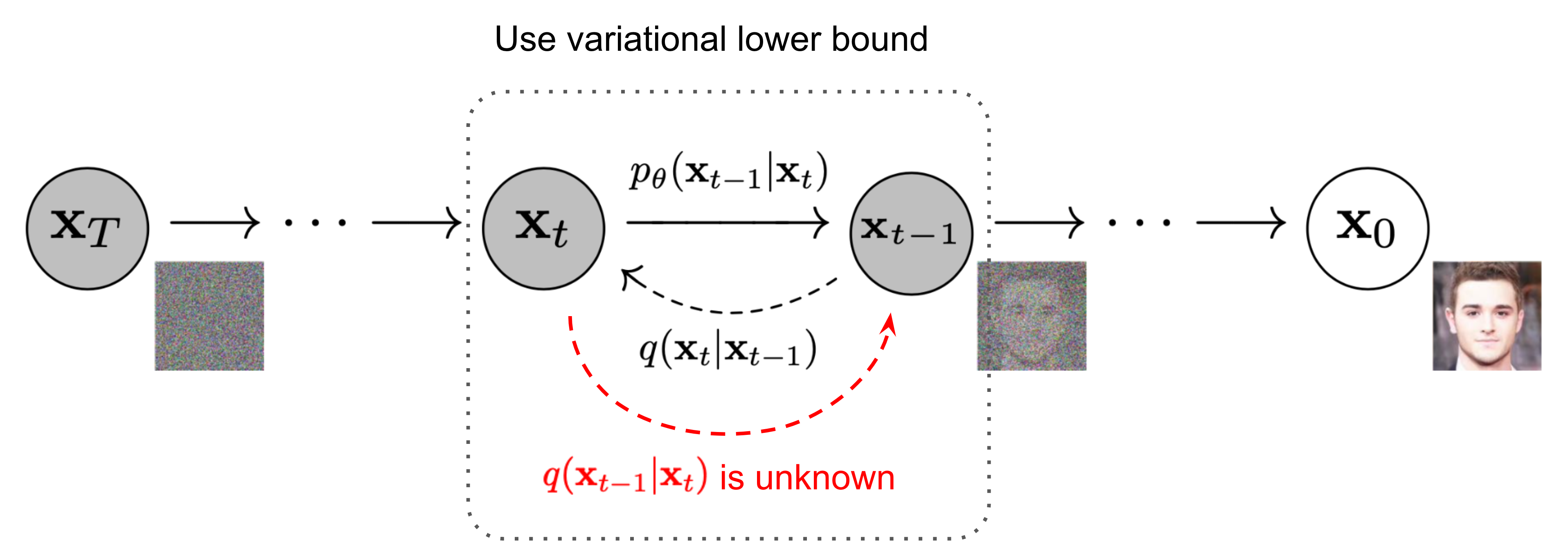
如果用概率学的写法（毕竟原文就自称扩散概率模型），我们的目标是要拟合出从xt\mathbf x_{t} 中去噪并还原出xt−1\mathbf x_{t-1} 的分布（去噪声操作）：

pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))pθ(x0:T)=p(xT)∏t=1Tpθ(xt−1∣xt)\begin{aligned} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) &= \mathcal{N}(\mathbf{x}_{t-1}; \boldsymbol{\mu}_\theta(\mathbf{x}_t, t), \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t))\\ p_\theta(\mathbf{x}_{0:T}) &= p(\mathbf{x}_T) \prod^T_{t=1} p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t) \end{aligned}

要达成这个目的，前提是先知道在现实分布q(⋅)q(\cdot) 中q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 的表达式（加噪声的逆操作），然后再设计一种损失函数（比如KL散度）最大化它们之间“分布相似度”（使得去噪声操作与加噪声的逆操作接近）。

有文献指出如果 q(xt∣xt−1)q(\mathbf{x}_{t} \vert \mathbf{x}_{t-1}) 满足高斯分布且 βt\beta_t 足够小，q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 仍然是一个高斯分布，所以我们可以假设它服从高斯分布。但是q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 还是没法直接得出，所以我们也没办法直接得到它的表达式了。好在如果已知训练集x0\mathbf x_0 我们可以推导出带有x0\mathbf x_0 条件的分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 的表达式，并且它也服从于高斯分布，不妨设

q(xt−1∣xt,x0)=N(xt−1;μ~(xt,x0),β~tI)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; {\color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0)}, {\color{red}{\tilde{\beta}_t} \mathbf{I}})

可以利用贝叶斯公式进行推导：

q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt−1∣x0)q(xt∣x0)∝exp⁡(−12((xt−αtxt−1)2βt+(xt−1−αˉt−1x0)21−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12(xt2−2αtxtxt−1+αtxt−12βt+xt−12−2αˉt−1x0xt−1+αˉt−1x021−αˉt−1−(xt−αˉtx0)21−αˉt))=exp⁡(−12((αtβt+11−αˉt−1)xt−12−(2αtβtxt+2αˉt−11−αˉt−1x0)xt−1+C(xt,x0)))\begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ q(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ q(\mathbf{x}_t \vert \mathbf{x}_0) } \\ &\propto \exp \Big(-\frac{1}{2} \big(\frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp \Big(-\frac{1}{2} \big(\frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t {\color{blue}{\mathbf{x}_{t-1}}} + \alpha_t {\color{red}{\mathbf{x}_{t-1}^2}} }{\beta_t} + \frac{ {\color{red}{\mathbf{x}_{t-1}^2}}{- 2 \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0} {\color{blue}{\mathbf{x}_{t-1}}}{+ \bar{\alpha}_{t-1} \mathbf{x}_0^2} }{1-\bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1-\bar{\alpha}_t} \big) \Big) \\ &= \exp\Big( -\frac{1}{2} \big( {\color{red}{(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2} - {\color{blue}{(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1}}{ + C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \end{aligned}

其中C(xt,x0)C(\mathbf{x}_t, \mathbf{x}_0) 是与xt−1\mathbf x_{t-1} 无关的函数。根据高斯分布函数，我们可以将红色部分重写成方差β~tI{\color{red}{\tilde{\beta}_t} \mathbf{I}} ，蓝色部分重写成期望μ~(xt,x0){\color{blue}{\tilde{\boldsymbol{\mu}}}(\mathbf{x}_t, \mathbf{x}_0)}，即

β~t=1/(αtβt+11−αˉt−1)=1/(αt−αˉt+βtβt(1−αˉt−1))=1−αˉt−11−αˉt⋅βtμ~t(xt,x0)=(αtβtxt+αˉt−11−αˉt−1x0)/(αtβt+11−αˉt−1)=(αtβtxt+αˉt−11−αˉt−1x0)1−αˉt−11−αˉt⋅βt=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉtx0\begin{aligned} \tilde{\beta}_t &= 1/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) = 1/(\frac{\alpha_t - \bar{\alpha}_t + \beta_t}{\beta_t(1 - \bar{\alpha}_{t-1})}) = {\color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t}} \\ \tilde{\boldsymbol{\mu}}_t (\mathbf{x}_t, \mathbf{x}_0) &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)/(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \\ &= (\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1} }}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0) {\color{green}{\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t}} \\ &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \mathbf{x}_0\\ \end{aligned}

此时再将 (★) 式代入，就可以把期望函数改写成

μ~t=αt(1−αˉt−1)1−αˉtxt+αˉt−1βt1−αˉt1αˉt(xt−1−αˉtϵt)=1αt(xt−1−αt1−αˉtϵt)\begin{aligned} \tilde{\boldsymbol{\mu}}_t &= \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} \mathbf{x}_t + \frac{\sqrt{\bar{\alpha}_{t-1}}\beta_t}{1 - \bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) \\ &={\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \end{aligned}

这样一来，我们就推导出了真实分布下的q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 。其中，方差的值相当于是定值，而期望表达式中含有的ϵt\boldsymbol{\epsilon}_t 才属于决定性因子。所以实际上我们的神经网络只需要学习噪声就好了，那么我们岂不是直接拟合这个噪声就可以了？所以我们推导这么久，还是需要设计类似下面的这个损失？

∥ϵt−ϵθ(xt,t)∥2\Vert\boldsymbol\epsilon_{t}-\boldsymbol\epsilon_\theta(\mathbf x_{t},t)\Vert^2

但是还有一个关键问题，这里是拟合带x0\mathbf x_0 条件的分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) ，而不是没有带上x0\mathbf x_0 的那个实际上最终要计算的分布q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 。这中间还是缺乏数学理论上的指导来建立桥梁。

回归正题，对于一个生成任务来说，我们最终的目的都是为了最大化(边缘)似然pθ(x0)p_{\theta}(\mathbf x_0)，其中

pθ(x0)=∫pθ(x0:T)dx1:Tp_{\theta}(\mathbf x_0)=\int p_{\theta}(\mathbf x_{0:T})\mathrm d\mathbf x_{1:T}

这个积分是很难直接去计算的，不过我们可以利用变分下界（variational lower bound，VLB. 也称 Evidence Lower Bound，ELBO，证据下界），找到pθ(x0)p_{\theta}(\mathbf x_0) 的对数下界，也即它负对数的上界（这部分的理论知识在本站介绍VAE的文章里也有相关阐释）。

−log⁡pθ(x0)≤−log⁡pθ(x0)+DKL(q(x1:T∣x0)∥pθ(x1:T∣x0)); KL is non-negative=−log⁡pθ(x0)+Ex1:T∼q(x1:T∣x0)[log⁡q(x1:T∣x0)pθ(x0:T)/pθ(x0)]=−log⁡pθ(x0)+Eq[log⁡q(x1:T∣x0)pθ(x0:T)+log⁡pθ(x0)]=Eq[log⁡q(x1:T∣x0)pθ(x0:T)]Let LVLB=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]≥−Eq(x0)log⁡pθ(x0)\begin{aligned} - \log p_\theta(\mathbf{x}_0) &\leq - \log p_\theta(\mathbf{x}_0) + D_\text{KL}(q(\mathbf{x}_{1:T}\vert\mathbf{x}_0) \| p_\theta(\mathbf{x}_{1:T}\vert\mathbf{x}_0) ) & \small{\text{; KL is non-negative}}\\ &= - \log p_\theta(\mathbf{x}_0) + \mathbb{E}_{\mathbf{x}_{1:T}\sim q(\mathbf{x}_{1:T} \vert \mathbf{x}_0)} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T}) / p_\theta(\mathbf{x}_0)} \Big] \\ &= - \log p_\theta(\mathbf{x}_0) + \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} + \log p_\theta(\mathbf{x}_0) \Big] \\ &= \mathbb{E}_q \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ \text{Let }L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log \frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \geq - \mathbb{E}_{q(\mathbf{x}_0)} \log p_\theta(\mathbf{x}_0) \end{aligned}

也就是说，我们只需要最小化LVLBL_\text{VLB} 就能间接实现优化pθ(x0)p_{\theta}(\mathbf x_0) 的任务。（该推导还可以用琴生不等式导出，详见 Lil’Log）

更进一步地，这里 VLB 的公式还可以继续展开，把我们前面推导出来的q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 用起来：

LVLB=Eq(x0:T)[log⁡q(x1:T∣x0)pθ(x0:T)]=Eq[log⁡∏t=1Tq(xt∣xt−1)pθ(xT)∏t=1Tpθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=1Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt∣xt−1)pθ(xt−1∣xt)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡(q(xt−1∣xt,x0)pθ(xt−1∣xt)⋅q(xt∣x0)q(xt−1∣x0))+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+∑t=2Tlog⁡q(xt∣x0)q(xt−1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[−log⁡pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)+log⁡q(xT∣x0)q(x1∣x0)+log⁡q(x1∣x0)pθ(x0∣x1)]=Eq[log⁡q(xT∣x0)pθ(xT)+∑t=2Tlog⁡q(xt−1∣xt,x0)pθ(xt−1∣xt)−log⁡pθ(x0∣x1)]=Eq[DKL(q(xT∣x0)∥pθ(xT))⏟LT+∑t=2TDKL(q(xt−1∣xt,x0)∥pθ(xt−1∣xt))⏟Lt−1−log⁡pθ(x0∣x1)⏟L0]\begin{aligned} L_\text{VLB} &= \mathbb{E}_{q(\mathbf{x}_{0:T})} \Big[ \log\frac{q(\mathbf{x}_{1:T}\vert\mathbf{x}_0)}{p_\theta(\mathbf{x}_{0:T})} \Big] \\ &= \mathbb{E}_q \Big[ \log\frac{\prod_{t=1}^T q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{ p_\theta(\mathbf{x}_T) \prod_{t=1}^T p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t) } \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=1}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t\vert\mathbf{x}_{t-1})}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \Big( \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)}\cdot \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1}\vert\mathbf{x}_0)} \Big) + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_t \vert \mathbf{x}_0)}{q(\mathbf{x}_{t-1} \vert \mathbf{x}_0)} + \log\frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big] \\ &= \mathbb{E}_q \Big[ -\log p_\theta(\mathbf{x}_T) + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} + \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{q(\mathbf{x}_1 \vert \mathbf{x}_0)} + \log \frac{q(\mathbf{x}_1 \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)} \Big]\\ &= \mathbb{E}_q \Big[ \log\frac{q(\mathbf{x}_T \vert \mathbf{x}_0)}{p_\theta(\mathbf{x}_T)} + \sum_{t=2}^T \log \frac{q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)}{p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t)} - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \Big] \\ &= \mathbb{E}_q [\underbrace{D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T))}_{L_T} + \sum_{t=2}^T \underbrace{D_\text{KL}(q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_{t-1} \vert\mathbf{x}_t))}_{L_{t-1}} \underbrace{- \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1)}_{L_0} ] \end{aligned}

整理一下就有：

LVLB=LT+LT−1+⋯+L0where LT=DKL(q(xT∣x0)∥pθ(xT))Lt=DKL(q(xt∣xt+1,x0)∥pθ(xt∣xt+1)) for 1≤t≤T−1L0=−log⁡pθ(x0∣x1)\begin{aligned} L_\text{VLB} &= L_T + L_{T-1} + \dots + L_0 \\ \text{where } L_T &= D_\text{KL}(q(\mathbf{x}_T \vert \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_T)) \\ L_t &= D_\text{KL}(q(\mathbf{x}_t \vert \mathbf{x}_{t+1}, \mathbf{x}_0) \parallel p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1})) \text{ for }1 \leq t \leq T-1 \\ L_0 &= - \log p_\theta(\mathbf{x}_0 \vert \mathbf{x}_1) \end{aligned}

其中，

  • LTL_T 这一项并不涉及到可学习的参数（xT∼N(0,I)\mathbf x_T\sim\mathcal{N}(0,\mathbf I) 与神经网络无关）所以可以直接忽略。
  • 对于L0L_0 ，原作者单独构建了一个离散编码器，服从N(x0;μθ(x1,1),Σθ(x1,1))\mathcal{N}(\mathbf{x}_0; \boldsymbol{\mu}_\theta(\mathbf{x}_1, 1), \boldsymbol{\Sigma}_\theta(\mathbf{x}_1, 1)) 来建模这个部分。
  • 最后是LtL_t，这个式子直接表明一个观点，我们想要神经网络学习出来的分布pθ(xt∣xt+1)p_\theta(\mathbf{x}_t \vert\mathbf{x}_{t+1}) 它需要拟合带x0\mathbf x_0 条件的分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) 。也就是说，通过 VLB 的推导，我们绕过了直接拟合q(xt−1∣xt)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 的困难性。

接下来是对LtL_t 的进一步化简，LtL_t 体现为计算两个正态分布的KL散度，这里有一个二级结论：

DKL(N(x;μx,Σx)∣∣N(y;μy,Σy))=12[log⁡∣Σy∣∣Σx∣−d+tr⁡(Σy−1Σx)+(μy−μx)TΣy−1(μy−μx)]D_{K L} \left( \mathcal{N} ( \boldsymbol{x} ; \boldsymbol{\mu}_{x}, \Sigma_{x} ) | | \mathcal{N} ( \boldsymbol{y} ; \boldsymbol{\mu}_{y}, \Sigma_{y} ) \right)=\frac{1} {2} \left[ \operatorname{l o g} \frac{| \Sigma_{y} |} {| \Sigma_{x} |}-d+\operatorname{t r} ( \Sigma_{y}^{-1} \Sigma_{x} )+( \boldsymbol{\mu}_{y}-\boldsymbol{\mu}_{x} )^{T} \Sigma_{y}^{-1} ( \boldsymbol{\mu}_{y}-\boldsymbol{\mu}_{x} ) \right]

其中dd 是向量x\boldsymbol x 的维度。所以，套用到LtL_t 就有：

Lt=Ex0,ϵ[12∥Σθ(xt,t)∥22∥μ~t(xt,x0)−μθ(xt,t)∥2]=Ex0,ϵ[12∥Σθ∥22∥1αt(xt−1−αt1−αˉtϵt)−1αt(xt−1−αt1−αˉtϵθ(xt,t))∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(xt,t)∥2]=Ex0,ϵ[(1−αt)22αt(1−αˉt)∥Σθ∥22∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| {\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Bigg[\frac{1}{2 \|\boldsymbol{\Sigma}_\theta \|^2_2} \bigg\| {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} - {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\boldsymbol{\epsilon}}_\theta(\mathbf{x}_t, t) \Big)} \bigg\|^2 \Bigg] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{ (1 - \alpha_t)^2 }{2 \alpha_t (1 - \bar{\alpha}_t) \| \boldsymbol{\Sigma}_\theta \|^2_2} \|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}

另外论文里还通过实验得出将前面的系数丢掉效果会更好，所以最终损失就逐渐变成了我们熟悉的版本（第二行将★式代入）：

Ltsimple=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(xt,t)∥2]=Et∼[1,T],x0,ϵt[∥ϵt−ϵθ(αˉtx0+1−αˉtϵt,t)∥2]\begin{aligned} L_t^\text{simple} &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\|^2 \Big] \\ &= \mathbb{E}_{t \sim [1, T], \mathbf{x}_0, \boldsymbol{\epsilon}_t} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}

训练和采样

最终可以给出 DDPM 的训练阶段和采样(生成)/推理阶段的算法流程：

其中，Sampling 的 Line 4 的推导如下：

μθ(xt,t)=1αt(xt−1−αt1−αˉtϵθ(xt,t))Thusxt−1∼N(xt−1;1αt(xt−1−αt1−αˉtϵθ(xt,t)),σtI)\begin{aligned} \boldsymbol{\mu}_\theta(\mathbf{x}_t, t) &= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big)} \\ \text{Thus}\quad\mathbf{x}_{t-1} &\sim \mathcal{N}\bigg(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \Big), \sigma_t\mathbf I\bigg) \end{aligned}

也就是这里生成xt−1\mathbf{x}_{t-1} 的方式仍然是从分布中采样出来的（亦即加上了额外的随机噪声σtz\sigma_t\bf z）而不是用固定的公式（用期望代替），这有助于控制生成效果的随机性和丰富性。关于这一点，台大李宏毅老师通过类比LLM和语音模型，说明随机性的加入对模型性能具有提升的效果，具体可以参考李老师的课程视频。李老师也谈了谈 Diffusion Models 能成功的原因，可能与 Auto-regressive 中再次融入 Auto-regressive 的思想有关系。

参数设置

在 DDPM 中，分布pθ(xt−1∣xt)p_\theta(\mathbf{x_{t-1}|\mathbf{x}_t}) 的方差Σθ(xt,t)=σt2I\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \sigma^2_t \mathbf{I} 中的σt2\sigma_t^2 直接采用前面我们推导出来的一个定值：

  • β~t=1−αˉt−11−αˉt⋅βt\tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t 论文称这种设置为 fixed-small，被用于CelebA-HQ 和 LSUN 数据集；
  • 或是直接用βt\beta_t ，称为 fixed-large，被用于 CIFAR-10 数据集；
  • 在 DDIM 中则使用σt(η)2=η⋅β~t\sigma_t(\eta)^2=\eta\cdot\tilde{\beta}_t，是fixed-small 版本在乘上一个超参数因子，0≤η≤10\leq\eta\leq1.

IDDPM（Improved Denoising Diffusion Probabilistic Models）则利用可学习的向量v\bf v 将βt\beta_t 和β~t\tilde{\beta}_t 混合插值作为最终的方差：

Σθ(xt,t)=exp⁡(vlog⁡βt+(1−v)log⁡β~t)\boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) = \exp(\mathbf{v} \log \beta_t + (1-\mathbf{v}) \log \tilde{\beta}_t)

IDDPM 指出当方差也可学习时（原版相当于只优化了均值），DDPM的 log-likelihood 可以进一步得到改进。

在随时间（1≤t≤T1\leq t\leq T）的变化上，DDPM 的设置方法是从β1=10−4\beta_1=10^{-4} 到βT=0.02\beta_T=0.02 的线性变化，与归一化图像像素值相比，它们相对较小。而 IDDPM 采用了一种基于余弦的调度策略（类比学习率）：

βt=clip(1−αˉtαˉt−1,0.999)αˉt=f(t)f(0)where f(t)=cos⁡(t/T+s1+s⋅π2)2\beta_t = \text{clip}(1-\frac{\bar{\alpha}_t}{\bar{\alpha}_{t-1}}, 0.999) \quad\bar{\alpha}_t = \frac{f(t)}{f(0)}\quad\text{where }f(t)=\cos\Big(\frac{t/T+s}{1+s}\cdot\frac{\pi}{2}\Big)^2

由于DDPM最终推导得到的损失LsimpleL_{\text{simple}} 是不依赖于Σθ\boldsymbol{\Sigma}_\theta 的，所以为了学习到向量v\bf v 的最优取值，IDDPM又把LVLBL_{VLB} 引入了回来，最终目标函数Lhybrid=Lsimple+λLVLBL_\text{hybrid} = L_\text{simple} + \lambda L_\text{VLB} ，其中λ=0.001\lambda=0.001.

模型架构

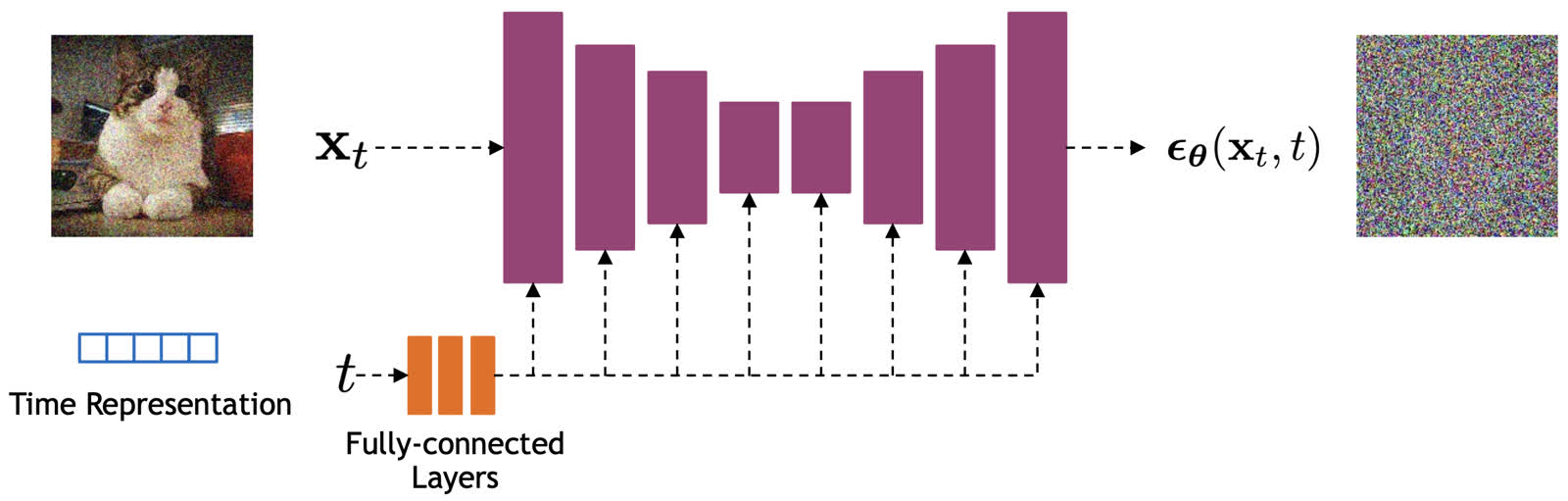
根据前面的推导可以发现，扩散模型用到神经网络的地方在于拟合噪声，具体来说就是接收一个噪声图 xt\mathbf x_t 和一个时间步 tt 作为参数，并输出一个噪声的预测结果 ϵθ(xt,t)\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)。

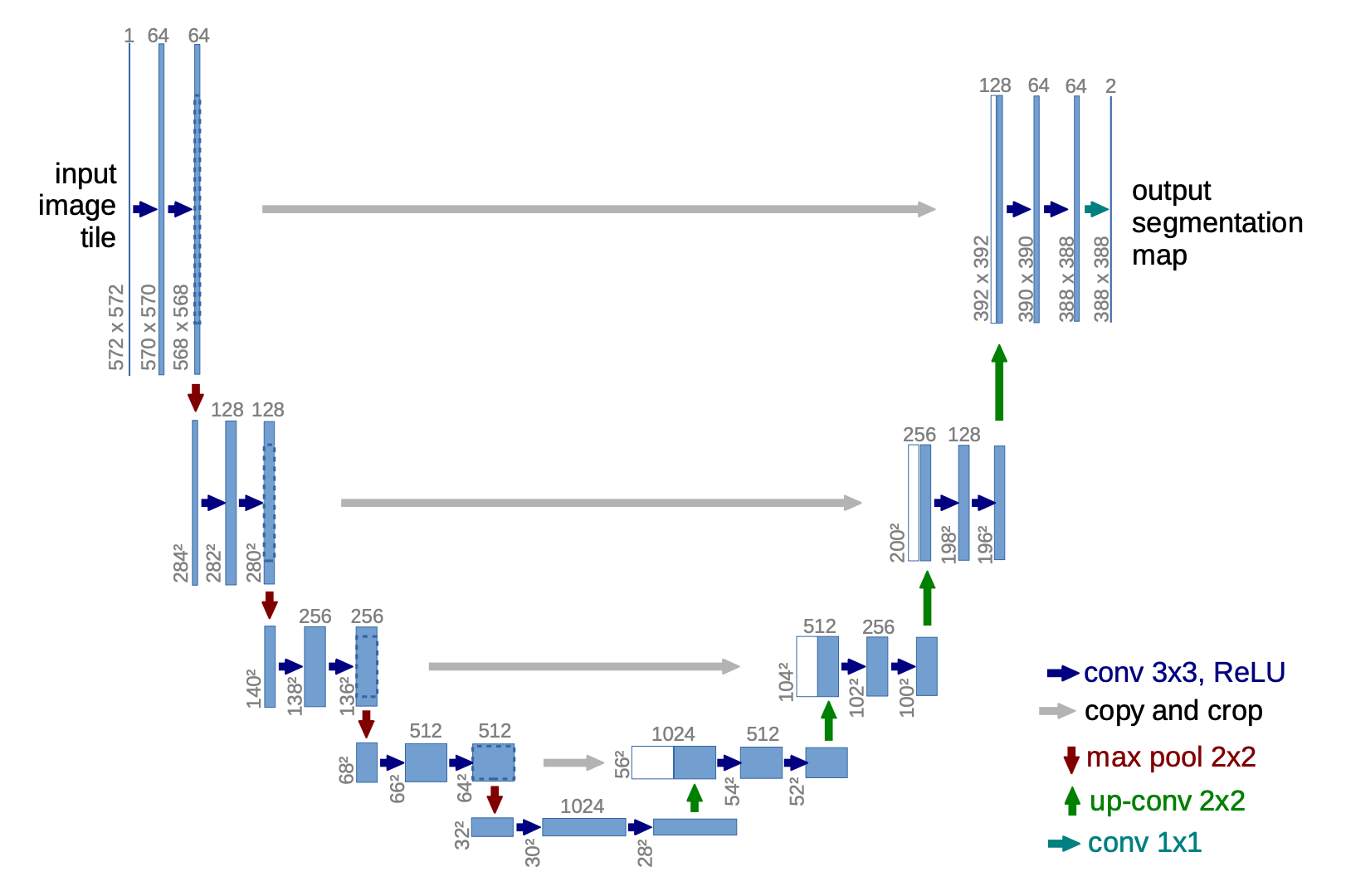
DDPM 用于预测噪声所使用的骨干网络主要是 U-Net。值得注意的是，对于时间，我们是先得到一个 Time Embedding 再将其和噪声图一起输入给 U-Net 的。这样做的理由是可以让 U-Net 根据输入变量tt 自动调整适应当前扩散时间步tt 的网络内部参数并输出对应的结果，扩展实现了在一个参数共享的 U-Net 内就实现共TT 个时间步的计算，而不是“一共构建TT 个参数不共享的 U-Net 网络然后手动在不同时间步调用不同的网络完成输出”。

U-Net (Ronneberger, et al. 2015) 是一种CNN模型，因其架构形状类似U型而得名。它包括两个阶段，下采样（Downsampling）和上采样（Upsampling），具体设置如下：

  • 下采样：每个步骤包含两次重复的3x3卷积操作（Unpadding），每次卷积后接 ReLU 和步长为 2 的 2×2 MaxPooling。在每个下采样步骤中，特征通道数量翻倍。
  • 上采样：每个步骤包含特征图的上采样操作，后接2×2卷积，每次操作将特征通道数量减半。
  • 跳接：通过将下采样每阶段得到的特征图拼接到对应的上采样阶段的特征图上，为上采样过程提供关键的高分辨率的特征。

加速采样 (DDIM)

DDPM的高质量生成依赖于较大的TT（一般为1000或以上），这导致Diffusion的前向过程非常缓慢。因此，为了加速 Diffusion Model 的前向过程，就得考虑如何缩短采样步长TT，但其实并非那么容易。

For example, it takes around 20 hours to sample 50k images of size 32 × 32 from a DDPM, but less than a minute to do so from a GAN on an Nvidia 2080 Ti GPU.

  • 直接将TT 设置得比较小是否可行？No.
    在前向过程中我们有xt=αtxt−1+1−αtϵt−1\mathbf x_t=\sqrt{\alpha_t} \mathbf{x}_{t-1}+\sqrt{1-\alpha_t}\boldsymbol{\epsilon}_{t-1}，并且希望αt\alpha_t 尽可能接近1以保证加微小噪声时保留大体原分布。最终还有xT=αˉTx0+1−αˉTϵ\mathbf{x}_T = \sqrt{\bar{\alpha}_T}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_T}\boldsymbol{\epsilon}，这一步我们希望xT\mathbf{x}_T 尽可能服从标准正态分布。要实现这一步，就要有αˉt=∏i=1Tαi\bar{\alpha}_t = \prod_{i=1}^T \alpha_i 尽可能为0。所以，每一项aia_i 都接近1的同时还想要它们的乘积接近0，唯一的方法只有TT 足够大。

  • 加噪时能否跳步而不是一步步来？No.
    虽然 DDPM 最终把优化目标简化成了噪声的MSE，但其根源是拟合反向的分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)，在推导它时我们是使用了贝叶斯公式结合q(xt∣xt−1)q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) 得到的。而后者这个分布服从马尔可夫链的假设。如果跳步便违反了这一假设。

DDIM（Denoising Diffusion Implicit Models）给出了一种解决方法来破解“不能跳步”的问题——干脆直接找一种不依赖于马尔可夫的（Non-Markovian）推导方法。

思路分析

在苏剑林老师的博客中给了一个很清晰的路线来归纳 DDPM 的推导：

q(xt∣xt−1)→推导q(xt∣x0)→推导q(xt−1∣xt,x0)→近似pθ(xt−1∣xt)q(\mathbf{x}_t|\mathbf{x}_{t-1})\xrightarrow{\text{推导}}q(\mathbf{x}_t|\mathbf{x}_0)\xrightarrow{\text{推导}}q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0)\xrightarrow{\text{近似}}p_\theta(\mathbf{x}_{t-1}|\mathbf{x}_t)

此外，还可以总结出如下规律：

  • 损失函数只依赖于q(xt∣x0)q(\mathbf{x}_t|\mathbf{x}_0)；
  • 采样过程只依赖于p(xt−1∣xt)p(\mathbf{x}_{t-1}|\mathbf{x}_t).

也就是说，优化目标的推导结果来看，它和依赖马尔可夫假设的q(xt∣xt−1)q(\mathbf{x}_t|\mathbf{x}_{t-1}) 没有关系，那么干脆一不做二不休直接不管它了！那没有q(xt∣xt−1)q(\mathbf{x}_t|\mathbf{x}_{t-1}) 如何用贝叶斯公式推导出q(xt−1∣xt,x0)q\left(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0\right) 呢？答案是不用贝叶斯了！

在 DDPM 中我们曾经假设过它服从于正态分布：

q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI) where μ~t(xt,x0):=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxt and β~t:=1−αˉt−11−αˉtβt\begin{aligned} q\left(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0\right) & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right), \tilde{\beta}_t \mathbf{I}\right) \\ \text { where } \quad \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) & :=\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0+\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t \quad \text { and } \quad \tilde{\beta}_t:=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \beta_t \end{aligned}

既然如此我们不如直接使用待定系数法把它定出来：

q(xt−1∣xt,x0)=N(xt−1;κtxt+λtx0,σt2I)q\left(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0\right) = \mathcal{N}(\mathbf{x}_{t-1}; \kappa_t \mathbf{x}_t + \lambda_t \mathbf{x}_0, \sigma_t^2 \mathbf{I})

其中，约束q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) 仍然与 DDPM 保持一致，亦即我们新设计的这个分布满足边缘分布条件：

∫q(xt−1∣xt,x0)q(xt∣x0)  dxt=q(xt−1∣x0)\int q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) q(\mathbf{x}_t|\mathbf{x}_0)\;\mathrm d\mathbf{x}_t = q(\mathbf{x}_{t-1}|\mathbf{x}_0)

事实上，满足这个边缘分布条件从采样的视角来看只需要联立下面的方程即可。

{xt=αˉtx0+1−αˉtϵt′xt−1=αˉt−1x0+1−αˉt−1ϵt−1′xt−1=(κtxt+λtx0)+σtϵ′, where ϵt′,ϵt−1′,ϵ′∼N(0,I)\begin{cases} \mathbf{x}_t &= \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t'\\ \mathbf{x}_{t-1} &= \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1}'\\ \mathbf{x}_{t-1} &= (\kappa_t \mathbf{x}_t + \lambda_t \mathbf{x}_0)+{\sigma}_{t}\boldsymbol{\epsilon}'\\ \end{cases} \quad\text{, where } \boldsymbol{\epsilon}_t',\boldsymbol{\epsilon}_{t-1}',\boldsymbol{\epsilon}'\sim\mathcal{N}(\mathbf 0,\mathbf I)

推导如下：

xt−1= κtxt+λtx0+σtϵ′= κt(αˉtx0+1−αˉtϵt′)+λtx0+σtϵ′= (κtαˉt+λt)x0+(κt1−αˉtϵt′+σtϵ′)= (κtαˉt+λt)x0+κt2(1−αˉt)+σt2ϵxt−1=αˉt−1x0+1−αˉt−1ϵt−1′\begin{aligned}\mathbf{x}_{t-1} =&\, \kappa_t \mathbf{x}_t + \lambda_t \mathbf{x}_0 + \sigma_t \boldsymbol{\epsilon}' \\ =&\, \kappa_t (\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t') + \lambda_t \boldsymbol{x}_0 + \sigma_t \boldsymbol{\epsilon}' \\ =&\, (\kappa_t \sqrt{\bar{\alpha}_t} + \lambda_t) \boldsymbol{x}_0 + (\kappa_t\sqrt{1 - \bar{\alpha}_t} \boldsymbol{\epsilon}_t' + \sigma_t \boldsymbol{\epsilon}') \\ =&\, (\kappa_t \sqrt{\bar{\alpha}_t} + \lambda_t) \boldsymbol{x}_0 + \sqrt{\kappa_t^2(1 - \bar{\alpha}_t) + \sigma_t^2}\boldsymbol{\epsilon}\\ \mathbf{x}_{t-1} =& \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_{t-1}}\boldsymbol{\epsilon}_{t-1}'\\ \end{aligned}

对应系数相等可以得到三元一次方程组：

{λt+κtαˉt=αˉt−1κt2(1−αˉt)+σt2=1−αˉt−1⇒(λt∗κt∗σt∗)=(αˉt−1−αˉt1−αˉt−1−σt21−αˉt1−αˉt−1−σt21−αˉtσt)\begin{cases} \lambda_t + \kappa_t\sqrt{\bar{\alpha}_t} = \sqrt{\bar{\alpha}_{t-1}} \\ \kappa_t^2(1 - \bar{\alpha}_t) + \sigma_t^2 = 1 - \bar{\alpha}_{t-1} \end{cases} \Rightarrow \begin{pmatrix} \lambda_t^* \\ \kappa_t^* \\ \sigma_t^* \end{pmatrix} = \begin{pmatrix} \sqrt{\bar{\alpha}_{t-1}} - \sqrt{\bar{\alpha}_t}\sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_t}} \\ \sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_t}} \\ \sigma_t \end{pmatrix}

三个未知数两个方程最终会有一个自由变量，这里我们取σt\sigma_t 为那个自由变量。也就是说我们最终会得到一簇解，这些解都满足约束条件。从而我们得到：

q(xt−1∣xt,x0)=N(xt−1;(αˉt−1−αˉt1−αˉt−1−σt21−αˉt)x0+(1−αˉt−11−αˉt)xt,σt2I)=N(xt−1;αˉt−1x0+1−αˉt−1−σt2xt−αˉtx01−αˉt,σt2I)\begin{aligned} q(\mathbf{x}_{t-1}|\mathbf{x}_t, \mathbf{x}_0) &= \mathcal{N}\left(\mathbf{x}_{t-1}; \left(\sqrt{\bar{\alpha}_{t-1}} - \sqrt{\bar{\alpha}_t}\sqrt{\frac{1-\bar{\alpha}_{t-1}-\sigma_t^2}{1-\bar{\alpha}_t}}\right)\mathbf{x}_0 + \left(\sqrt{\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t}}\right)\mathbf{x}_t, \sigma_t^2\mathbf{I}\right) \\ &=\mathcal{N}\left(\mathbf{x}_{t-1}; \sqrt{\bar{\alpha}_{t-1}}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_{t-1}-\sigma_t^2}\frac{\mathbf{x}_t - \sqrt{\bar{\alpha}_t}\mathbf{x}_0}{\sqrt{1-\bar{\alpha}_t}}, \sigma_t^2\mathbf{I}\right) \end{aligned}

当σt2\sigma_t^2 选取不同的值时我们就能得到不同的更为灵活的分布，DDIM 论文里取其为依赖一个超参数因子η\eta 的σt(η)2=η⋅β~t\sigma_t(\eta)^2=\eta\cdot\tilde{\beta}_t，它是 DDPM 提到的fixed-small 版本的一个扩展版本。值得一提的是，当η=1\eta=1 时得到的结果就等价于原始的 DDPM，而取η=0\eta=0 时就能得到一个确定性的采样过程，添加的随机噪声项为0。

作者针对其取值做了实验，最终得出取0时的效果最优，所以取0的版本才被正式冠以 denoising diffusion implicit model（DDIM）之名。

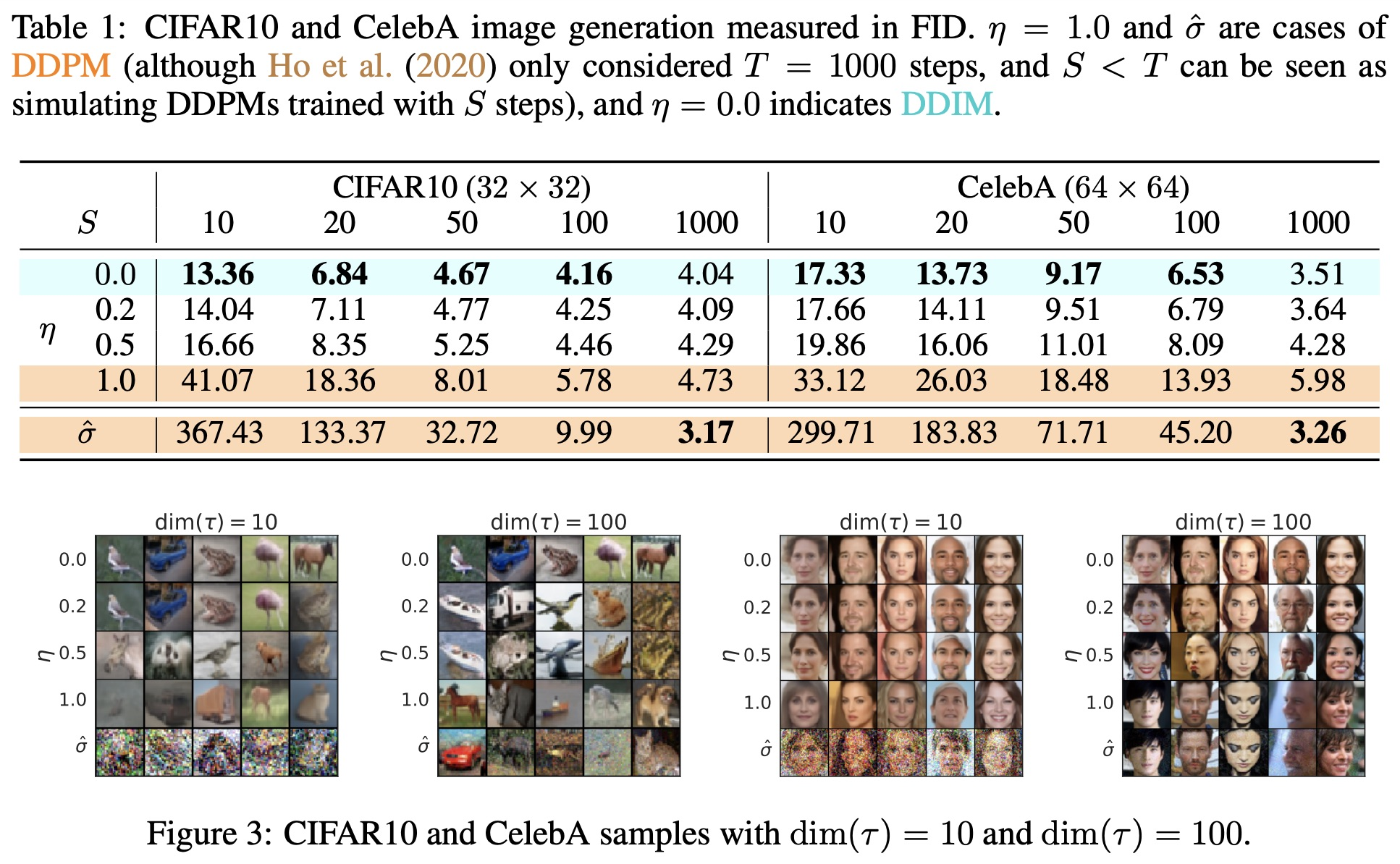
由于 DDIM 只在对采样q(xt−1∣xt,x0)q\left(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0\right) 做了调整，并且没有影响到对损失函数的计算，所以 DDIM 甚至可以完美地继承了 DDPM 的训练过程，只是修改了一下采样方式。这也为 DDIM 可以实现加速提供了可能。

加速策略

由于DDIM抛去了马尔可夫链假设，所以加速的思路也就很简单了，跳步策略直接成为了可行方案。设τ=[τ1,τ2,…,τdim⁡(τ)]\boldsymbol{\tau} = [\tau_1,\tau_2,\dots,\tau_{\dim(\boldsymbol{\tau})}] 是原来序列[1,2,⋯ ,T][1,2,\cdots,T] 的任意子序列，我们可以用αˉτ1,αˉτ2,⋯ ,αˉdim⁡(τ)\bar{\alpha}_{\tau_1},\bar{\alpha}_{\tau_2},\cdots,\bar{\alpha}_{\dim(\boldsymbol{\tau})} 为参数训练一个扩散步数为dim(τ)\text{dim}(\tau) 的 DDPM。它的目标函数是原版扩散步数是TT 的 DDPM 的目标函数的子集。

没了马尔可夫限制，采样时我们有：

qσ,s<t(xs∣xt,x0)=N(xs;αˉs(xt−1−αˉtϵθ(t)(xt)αˉt)+1−αˉs−σt2ϵθ(t)(xt),σt2I)q_{\sigma, s < t}(\mathbf{x}_s \vert \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_s; \sqrt{\bar{\alpha}_s} \Big( \frac{\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t} \epsilon^{(t)}_\theta(\mathbf{x}_t)}{\sqrt{\bar{\alpha}_t}} \Big) + \sqrt{1 - \bar{\alpha}_s - \sigma_t^2} \epsilon^{(t)}_\theta(\mathbf{x}_t), \sigma_t^2 \mathbf{I})

其中，ϵθ(t)(.)\epsilon^{(t)}_\theta(.) 代表模型从xt\mathbf{x}_t 中预测的噪声。上式是由 DDIM 的采样分布中将x0\mathbf x_0 替换成模型通过xt\mathbf x_t 推导并预测的，即有：x0=1αˉt(xt−1−αˉtϵθ)\mathbf x_0=\frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_\theta).

论文给出了不同的采样步长的生成效果（同样见上图）。可以看到DDIM在较小采样步长时就能达到较好的生成效果。如 CIFAR10 数据集中，S=50S=50 就达到了S=1000S=1000 的90%的效果，与之相比DDPM只能达到10%左右的FID效果。可见DDPM在推导采样分布中用了马尔可夫假设的确限制了它的采样间隔。

语义插值效应

因为 DDIM 将σt\sigma_t 设为了00，这让采样过程是确定的，只受xT\mathbf{x}_T 的​影响，具有采样一致性(sample consistency)。作者发现，当给定xT\mathbf{x}_T​ 时不同的的采样时间序列τ\tau 所生成图片都很相近，这说明​似乎可以将其视作所生成的图片的隐编码信息。

有个小trick，我们在实际的生成中可以先设置较小的采样步长进行生成，若生成的图片是我们想要的，则用较大的步长重新生成高质量的图片。

即然xT\mathbf{x}_T​ 可能是生成图片的隐空间编码，那么它是否具备其它隐概率模型（如GAN）所观察到的语义插值效应呢？

首先从高斯分布采样两个随机变量xT(0),xT(1)\mathbf{x}_T^{(0)},\mathbf{x}_T^{(1)}​ ，并用他们做图像生成得到下图最左侧与最右侧的结果。随后用球面线性插值方法（spherical linear interpolation，Slerp）对xT(0),xT(1)\mathbf{x}_T^{(0)},\mathbf{x}_T^{(1)} 进行插值，得到一系列中间结果：

xT(α)=sin⁡((1−α)θ)sin⁡(θ)xT(0)+sin⁡(αθ)sin⁡(θ)xT(1)\mathbf{x}_{T}^{( \alpha)}=\frac{\sin( ( 1-\alpha) \theta)} {\sin( \theta)} \mathbf{x}_{T}^{(0)}+\frac{\sin( \alpha\theta)} {\sin( \theta)} \mathbf{x}_{T}^{(1)}

其中θ=arccos⁡((xT(0))TxT(1)∥xT(0)∥⋅∥xT(1)∥)\theta=\operatorname{arccos} \left( \frac{(\mathbf{x}_{T}^{(0)} )^{T} x_{T}^{(1)}} {\Vert\mathbf{x}_{T}^{(0)}\Vert\cdot \Vert\mathbf{x}_{T}^{(1)}\Vert} \right)

最终发现，从左图像的生成结果插值过渡到另一个图像的过程中，图像内容会在逐渐保留其原始语义特征的情况下过渡，亦即 DDIM 具有语义插值效应。

和分数模型的联系

条件控制 (Condition)

作为生成模型，扩散模型跟 VAE、GAN、Flow 等模型的发展史很相似，都是先出来了无条件生成，然后有条件生成就紧接而来。无条件生成往往是为了探索效果上限，而有条件生成则更多是应用层面的内容，因为它可以实现根据我们的意愿（给定的某种条件）来控制模型输出我们想要的结果。

从方法上来看，条件控制生成的方式分两种：

  • Classifier-Guidance：事后修改。可以复用已训练好的无条件生成模型，在此基础上通过一个可学习的分类器控制条件生成。该方案的训练成本比较低，但是推断成本会高些，而且控制细节上通常没那么到位；
  • Classifier-Free：事前训练。直接在扩散模型的训练过程中就加入条件信号最终实现条件生成的目的。

Classifier-Guidance

Classifier-Guidance 最早出自《Diffusion Models Beat GANs on Image Synthesis》，最初就是用来实现按类生成的；后来《More Control for Free! Image Synthesis with Semantic Diffusion Guidance》推广了“Classifier”的概念，使得它也可以按图、按文来生成。

从数学上来说， 带条件y\boldsymbol y 的生成相当于在扩散模型的生成过程p(xt−1∣xt)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) 中引入额外的条件，形成p(xt−1∣xt,y)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y})。而为了能沿用已训练好的生成模型（而不是重新训练模型），我们可以使用贝叶斯公式把p(xt−1∣xt)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t) 单独拆出来：

p(xt−1∣xt,y)=p(xt−1∣xt)p(y∣xt−1,xt)p(y∣xt)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)p(\boldsymbol{y}|\boldsymbol{x}_{t-1}, \boldsymbol{x}_t)}{p(\boldsymbol{y}|\boldsymbol{x}_t)}

又因为在前向过程（加噪过程）时xt\boldsymbol{x}_t 是由xt−1\boldsymbol{x}_{t-1} 加噪得来的，该过程与y\boldsymbol{y} 无关，所以p(xt∣xt−1,y)=p(xt∣xt−1)p(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1},\boldsymbol{y})=p(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}) ，进而有：

p(y∣xt−1,xt)=p(xt∣xt−1,y)p(y∣xt−1)p(xt∣xt−1)=p(xt∣xt−1)p(y∣xt−1)p(xt∣xt−1)=p(y∣xt−1)\begin{aligned} p(\boldsymbol y|\boldsymbol x_{t-1},\boldsymbol x_{t})&=\frac{p(\boldsymbol x_{t}|\boldsymbol x_{t-1}, \boldsymbol y)p(\boldsymbol y|\boldsymbol x_{t-1})}{p(\boldsymbol x_{t}|\boldsymbol x_{t-1})}\\ &= \frac{p(\boldsymbol x_{t}|\boldsymbol x_{t-1})p(\boldsymbol y|\boldsymbol x_{t-1})}{p(\boldsymbol x_{t}|\boldsymbol x_{t-1})}\\ &= p(\boldsymbol y|\boldsymbol x_{t-1}) \end{aligned}

上述等式p(y∣xt−1,xt)=p(y∣xt−1)p(\boldsymbol{y}|\boldsymbol{x}_{t-1}, \boldsymbol{x}_t)=p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) 还可以直观理解为：因为xt\boldsymbol{x}_t 是由xt−1\boldsymbol{x}_{t-1} 加噪得来的，所以在(xt−1,xt)(\boldsymbol{x}_{t-1}, \boldsymbol{x}_{t}) 的条件下y\boldsymbol{y} 的概率与只在xt−1\boldsymbol{x}_{t-1} 条件下y\boldsymbol{y} 的概率一样。

最终我们需要的生成过程可调整如下：

p(xt−1∣xt,y)=p(xt−1∣xt)p(y∣xt−1)p(y∣xt)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \frac{p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)p(\boldsymbol{y}|\boldsymbol{x}_{t-1})}{p(\boldsymbol{y}|\boldsymbol{x}_t)}

写成log⁡\log 的形式：

log⁡p(xt−1∣xt,y)=log⁡p(xt−1∣xt)+log⁡p(y∣xt−1)−log⁡p(y∣xt)\log p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \log p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)+\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1})-\log p(\boldsymbol{y}|\boldsymbol{x}_t)

考虑到当TT 足够大时，xt\boldsymbol{x}_t 与xt−1\boldsymbol{x}_{t-1} 足够接近，此时对后两项泰勒展开就有：

log⁡p(y∣xt−1)−log⁡p(y∣xt)≈(xt−1−xt)⋅∇xtlog⁡p(y∣xt)\log p(\boldsymbol{y}|\boldsymbol{x}_{t-1}) - \log p(\boldsymbol{y}|\boldsymbol{x}_t)\approx (\boldsymbol{x}_{t-1} - \boldsymbol{x}_t)\cdot\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)

又 DDPM 中有p(xt−1∣xt)=N(xt−1;μ(xt),σt2I)∝e−∥xt−1−μ(xt)∥2/2σt2p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)=\mathcal{N}(\boldsymbol{x}_{t-1};\boldsymbol{\mu}(\boldsymbol{x}_t),\sigma_t^2\mathbf{I})\propto e^{-\Vert \boldsymbol{x}_{t-1} - \boldsymbol{\mu}(\boldsymbol{x}_t)\Vert^2/2\sigma_t^2}，将这两式代入原方程，就有：

log⁡p(xt−1∣xt,y)=−12σt2∥xt−1−μ(xt)∥2+(xt−1−xt)∇xtlog⁡p(y∣xt)+C1=−12σt2∥xt−1−μ(xt)−σt2∇xtlog⁡p(y∣xt)∥2+C1+C2=log⁡p(z)+C\begin{aligned} \log{p(\boldsymbol x_{t-1}|\boldsymbol x_{t}, \boldsymbol y)} &= -\frac{1}{2\sigma_{t}^{2}}\|\boldsymbol x_{t-1}-\boldsymbol{\mu}(\boldsymbol x_t)\|^{2}+(\boldsymbol x_{t-1}-\boldsymbol x_{t})\nabla_{\boldsymbol x_{t}}\log{p(\boldsymbol y|\boldsymbol x_{t})}+C_{1} \\ &= -\frac{1}{2\sigma_{t}^{2}}\|\boldsymbol x_{t-1}-\boldsymbol{\mu}(\boldsymbol x_t)-\sigma_{t}^{2}\nabla_{\boldsymbol x_{t}}\log{p(\boldsymbol y|\boldsymbol x_{t})}\|^{2}+C_{1}+C_{2}\\ &= \log{p(z)}+C \end{aligned}

这里的C,C1,C2C,C_1,C_2 均为常数，具体来说是与xt−1\boldsymbol{x}_{t-1} 无关的式子。因为log⁡p(xt−1∣xt,y)\log{p(\boldsymbol x_{t-1}|\boldsymbol x_{t}, \boldsymbol y)} 本质上是关于xt−1\boldsymbol{x}_{t-1} 的函数f(xt−1)f(\boldsymbol{x}_{t-1})，并且为了凑出正态分布的形状需要把部分项移动到∥⋅∥2\|\cdot\|^2 内，所以做以上变换。

如此一来，我们就可以得到p(xt−1∣xt,y)∝p(z)p(\boldsymbol x_{t-1}|\boldsymbol x_{t}, \boldsymbol y)\propto p(\boldsymbol{z}) 仍服从于正态分布，其均值为μ(xt)+σt2∇xtlog⁡p(y∣xt)\mu(\boldsymbol x_t)+\sigma_{t}^{2}\nabla_{\boldsymbol x_{t}}\log{p(\boldsymbol y|\boldsymbol x_{t})}，方差仍然可以是σt2\sigma_t^2，亦即生产过程的采样可以用下式表达：

xt−1=μ(xt)+σt2∇xtlog⁡p(y∣xt)⏟New Item+σtϵ,ϵ∼N(0,I)\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) {\color{skyblue}{+\underbrace{\sigma_t^2 \nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t)}_{\text{New Item}}}} + \sigma_t\boldsymbol{\epsilon},\quad \boldsymbol{\epsilon}\sim \mathcal{N}(\boldsymbol{0},\mathbf{I})

与原始的扩散模型相比只需增加一项即可。

此外，原作者还指出往分类器的梯度中引入一个缩放参数γ\gamma，可以更好地调节生成效果：

xt−1=μ(xt)+σt2γ∇xtlog⁡p(y∣xt)+σtϵ,ϵ∼N(0,I)\boldsymbol{x}_{t-1} = \boldsymbol{\mu}(\boldsymbol{x}_t) +\sigma_t^2 {\color{skyblue}{\gamma}}\nabla_{\boldsymbol{x}_t} \log p(\boldsymbol{y}|\boldsymbol{x}_t) + \sigma_t\boldsymbol{\epsilon},\quad \boldsymbol{\epsilon}\sim \mathcal{N}(\boldsymbol{0},\mathbf{I})

当γ>1\gamma\gt1 时，生成过程将使用更多的分类器信号，结果将会提高生成结果与输入信号γ\gamma 的相关性，但是会相应地降低生成结果的多样性；反之，则会降低生成结果与输入信号之间的相关性，但增加了多样性。

Classifier-Guidance 的推导同样还可以用 Score function 来理解，会更加清晰和直观。并且采用这种推导方式解决了σt≠0\sigma_t\neq0 的局限性，从 DDPM 中推广到 DDIM（DDIM为确定性生成，σt=0\sigma_t=0），这里不再赘述。

Classifier-Free

Classifier-Free 方案本身没什么理论上的技巧，它是条件扩散模型最朴素的方案，出现得晚只是因为重新训练扩散模型的成本较大吧，在数据和算力都比较充裕的前提下，Classifier-Free方案表现出了令人惊叹的细节控制能力。

具体来说，该方案直接假设：

p(xt−1∣xt,y)=N(xt−1;μ(xt,y),σt2I)p(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t, \boldsymbol{y}) = \mathcal{N}(\boldsymbol{x}_{t-1}; \boldsymbol{\mu}(\boldsymbol{x}_t, \boldsymbol{y}),\sigma_t^2\mathbf{I})

与 DDPM 类似，条件y\boldsymbol{y} 在均值函数μ()\boldsymbol{\mu}() 里实际上也是放在噪声预测网络ϵθ()\boldsymbol{\epsilon}_\theta() 里作为网络模型的输入的， 即：

μ(xt,y)=1αt(xt−1−αt1−αˉtϵθ(xt,y,t))\boldsymbol{\mu}(\boldsymbol{x}_t, \boldsymbol{y}) = {\frac{1}{\sqrt{\alpha_t}} \Big( \boldsymbol{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, \boldsymbol{y},t) \Big)}

值得一提的是，Classifier-Guidance 中的均值函数：μ(xt)+σt2∇xtlog⁡p(y∣xt)\boldsymbol{\mu}(\boldsymbol x_t)+\sigma_{t}^{2}\nabla_{\boldsymbol x_{t}}\log{p(\boldsymbol y|\boldsymbol x_{t})} 可以视为 Classifier-Free 中μ(xt,y)\boldsymbol{\mu}(\boldsymbol{x}_t, \boldsymbol{y}) 的特殊情况。

此外，Classifier-Free 也应用了缩放机制，设置一个参数λ\lambda 来平衡相关性与多样性，将有条件生成的部分和无条件生成的部分组合起来。最终可以写为：

ϵ~θ(xt,y,t)=λϵθ(xt,y,t)+(1−λ)ϵθ(xt,t)\tilde{\boldsymbol{\epsilon}}_\theta(\boldsymbol{x}_t, \boldsymbol{y},t)=\lambda\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, \boldsymbol{y},t)+(1-\lambda)\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t,t)

这样一来看似需要学习两种模型，但实际上要实现无条件生成，不一定要去掉额外的条件输入，直接把条件输入替换成某个固定的空值∅\varnothing（例如 0）也是可以的。这样，有条件和无条件就被统一成了同一个模型 ϵθ(xt,y,t)\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, \boldsymbol{y},t)，当 y=∅\boldsymbol{y}=\varnothing 时就是代表无条件的情况。在联合训练时会以一定的概率将条件输入c\bf c 替换为 ∅\varnothing，使得模型能学习到两种情况。

下面是论文中给出的训练算法和采样算法：

Classifier-Free 的推导也可以用 Score function 来与 Classifier-Guidance 进一步联系起来，简单来说它通过一个隐式 分类器来替代Classifier-Guidance中的显式分类器，从而无需直接计算分类器及其梯度。

潜在扩散 (LDM)

之前的扩散模型（包括DDPM、DDIM以及其他我们没有介绍到的变体）一直面临着采样空间太大，学习的噪声维度和图像的维度同样大尺寸的问题。因此利用扩散模型进行高分辨率图像生成时，需要的计算资源会急剧增加，虽然 DDIM 等工作已经对此有所改善，但效果依然有限。

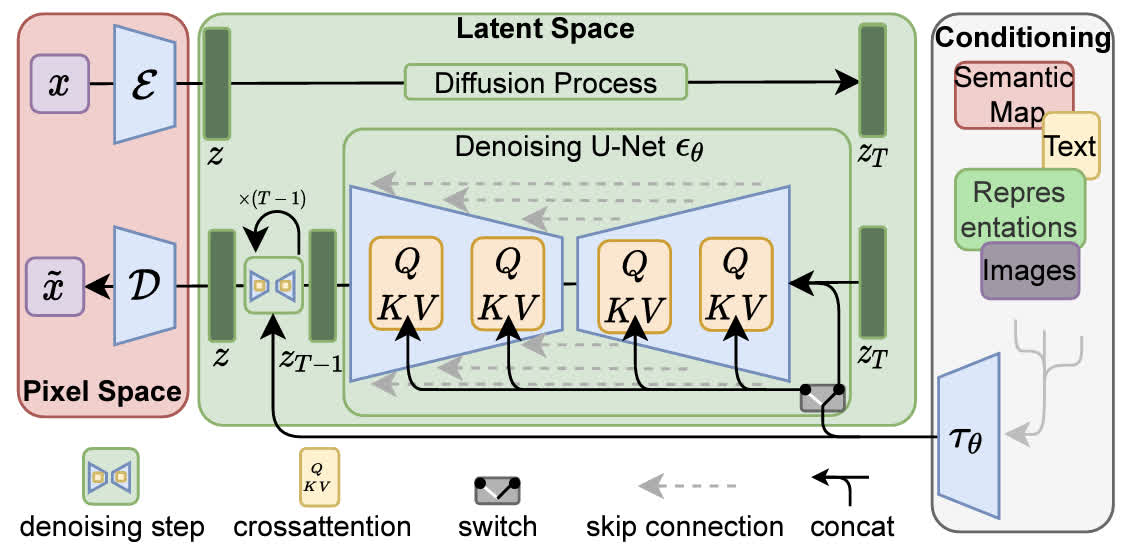
对此，LDM（Latent Diffusion Model）先使用一个预训练好的 AutoEncoder，将图片像素转换到了维度较小的 Latent Space 上，而后再进行传统的扩散模型推理与优化。这种训练方式使得 LDM 在算力和性能之间得到了平衡。

此外，通过引入交叉注意力，使得 DMs 能够在条件生成上有不错的效果，包括如文生图（text-to-image），图像修复（inpainting） 等。

它也是大名鼎鼎的 Stable Diffusion 的核心架构。Stable Diffusion 正是在这个通用架构的基础上进行了实现和训练得来的， 推动了生成式扩散模型在工程上的应用。

图像感知压缩

如前文所述，LDM 把图像生成过程从原始的图像像素空间转换到了一个隐空间。具体来说，对于一个维度为 x∈RH×W×3\mathbf{x}\in\mathbb{R}^{H\times W\times3} 的 RGB 图像，使用一个基于 VAE 的 encoder E\mathcal{E} 将其转换为隐变量 z=E(x)\mathbf{z}=\mathcal{E}(\mathbf{x})，之后便可以用对应的 decoder D\mathcal D 将其从隐变量转换回像素空间 x~=D(E(x))\tilde{\mathbf{x}}=\mathcal{D}(\mathcal{E}(\mathbf{x}))。

为了防止压缩后的空间是某个高方差的空间，需要进行正则化。作者给出了两种正则化方案：第一种是 KL-正则化，也就是将隐变量和标准高斯分布使用一个 KL 惩罚项进行正则化；第二种是 VQ-正则化，也就是使用一个 Vector Quantization 层进行正则化。

Encoding 涉及到下采样，作者测试了一系列下采样倍数 f∈{1,2,4,8,16,32}f\in\{1, 2, 4, 8, 16, 32\}，发现下采样 4-16 倍的时候可以比较好地权衡效率和质量。

你可能会产生这样的疑惑：既然LDM首先就利用了VAE得到 Latent Space 的 encoding，根据VAE的思想，这个 encoding 不就天然已经服从于标准高斯分布了吗？在它的基础上继续做 Diffusion 的意义在哪里？

实际上 LDM 中对 VAE 的 KL-正则化 前面的系数因子其实是很小很小的（1e-6），换句话说 LDM 中 VAE 基本上是当做简单的 AE 来用。（相关链接：Kylin的回答 - 知乎）

条件注入

LDM并没有在 Diffusion 的设计上做什么技术上的改进，仅仅只是将原始的优化目标调整到隐空间中。

LDM=Ex,ϵ∼N(0,1),t[∣∣ϵ−ϵθ(xt,t)∣∣22]LLDM=EE(x),ϵ∼N(0,1),t[∣∣ϵ−ϵθ(xt,t)∣∣22]\begin{aligned} L_\textrm{DM}&=\mathbb{E}_{\mathbf{x},\epsilon\sim\mathcal{N}(0,1),t}\left[||\epsilon-\epsilon_\theta(\mathbf{x}_t,t)||_2^2\right]\\ L_\textrm{LDM}&=\mathbb{E}_{\textcolor{red}{\mathcal{E}(\mathbf{x})},\epsilon\sim\mathcal{N}(0,1),t}\left[||\epsilon-\epsilon_\theta(\mathbf{x}_t,t)||_2^2\right] \end{aligned}

部分代码解析

此处所给代码均摘自 LDM 官方的 Pytorch 实现 CompVis/latent-diffusion，根据理解有所简化并给出了中文注释.

DDPM

构造函数

DDPM 类是 lightning.LightningModule 的派生类，因此继承了 cpkt_path、ignore_keys、train_step 等相关方法，由于本解析只说明关键部分，所以略去了对其的代码展示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class DDPM(pl.LightningModule):
    def __init__(self,
                 unet_config,
                 timesteps=1000,
                 beta_schedule="linear",
                 loss_type="l2",
                 clip_denoised=True,
                 linear_start=1e-4, # beta_0
                 linear_end=2e-2, # beta_T
                 cosine_s=8e-3, 
                 given_betas=None,
                 original_elbo_weight=0., 
                 v_posterior=0.,   # weight for choosing posterior variance as sigma = (1-v) * beta_tilde + v * beta
                 parameterization="eps",  # all assuming fixed variance schedules
                 l_simple_weight=1.,
                 learn_logvar=False,
                 logvar_init=0.,
                 ):
        super().__init__()

		# 模型是预测噪声还是直接预测x0
		assert parameterization in ["eps", "x0"], 'currently only supporting "eps" and "x0"' 
		self.parameterization = parameterization
		
		# 是否将噪音裁剪至 (−1.0 ,1.0) 区间. (默认值 True)
        self.clip_denoised = clip_denoised

		# 噪声预测模型（可带条件）
        self.image_size = image_size
        self.channels = channels
        self.use_positional_encodings = use_positional_encodings
        self.model = DiffusionWrapper(unet_config, conditioning_key)

		# weight for choosing posterior variance as sigma = (1-v) * beta_tilde + v * beta
        self.v_posterior = v_posterior
        # 损失函数中使用原始证据下界 (ELBO) 的权重
        self.original_elbo_weight = original_elbo_weight
        # 简单损失函数的权重和类型
        self.l_simple_weight = l_simple_weight
        self.loss_type = loss_type
        
		# 注册 beta 和 alpha，详见下文
        self.register_schedule(given_betas=given_betas, beta_schedule=beta_schedule, timesteps=timesteps,
                               linear_start=linear_start, linear_end=linear_end, cosine_s=cosine_s)

        
        
		# 使用可学习的方差
        self.learn_logvar = learn_logvar
        self.logvar = torch.full(fill_value=logvar_init, size=(self.num_timesteps,))
        if self.learn_logvar:
            self.logvar = nn.Parameter(self.logvar, requires_grad=True)
DiffusionWarpper

其中的 DiffusionWrapper 为预测噪声的模型，通常是 UNet，为了实现带条件或不带条件以及带条件的方式，单独封装了这个类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class DiffusionWrapper(pl.LightningModule):
    def __init__(self, net_config, conditioning_key):
        super().__init__()
        self.diffusion_model = UNetModel(net_config)
        self.conditioning_key = conditioning_key
        assert self.conditioning_key in [None, 'concat', 'crossattn', 'hybrid', 'adm']

    def forward(self, x, t, c_concat: list = None, c_crossattn: list = None):
        if self.conditioning_key is None:
            out = self.diffusion_model(x, t)
        elif self.conditioning_key == 'concat':
            xc = torch.cat([x] + c_concat, dim=1)
            out = self.diffusion_model(xc, t)
        elif self.conditioning_key == 'crossattn':
            cc = torch.cat(c_crossattn, 1)
            out = self.diffusion_model(x, t, context=cc)
        elif self.conditioning_key == 'hybrid':
            xc = torch.cat([x] + c_concat, dim=1)
            cc = torch.cat(c_crossattn, 1)
            out = self.diffusion_model(xc, t, context=cc)
        elif self.conditioning_key == 'adm':
            cc = c_crossattn[0]
            out = self.diffusion_model(x, t, y=cc)
        else:
            raise NotImplementedError()

        return out

注册β\beta 和α\alpha 时间表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
  def register_schedule(self, given_betas=None, beta_schedule="linear", timesteps=1000,
                        linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):

# 直接使用一组指定的 beta
      if given_betas:
          betas = given_betas
      # 否则按指定类型生成 beta
      # 类型可选 "linear"、"cosine"、"sqrt_linear" 或 "sqrt"
      else:
          betas = make_beta_schedule(beta_schedule, timesteps, linear_start=linear_start, linear_end=linear_end, cosine_s=cosine_s)

# 计算 alpha 和 对应的累积
# alphas_cumprod_prev 是 alphas_cumprod 的右移版本
      alphas = 1. - betas
      alphas_cumprod = np.cumprod(alphas, axis=0)
      alphas_cumprod_prev = np.append(1., alphas_cumprod[:-1])

      timesteps, = betas.shape
      self.num_timesteps = int(timesteps)
      self.linear_start = linear_start
      self.linear_end = linear_end
      assert alphas_cumprod.shape[0] == self.num_timesteps, 'alphas have to be defined for each timestep'

      to_torch = partial(torch.tensor, dtype=torch.float32)

# 将相关结果存入寄存器/缓冲区
# 缓冲区不会被视作模型参数, 不参与梯度更新
      self.register_buffer('betas', to_torch(betas))
      self.register_buffer('alphas_cumprod', to_torch(alphas_cumprod))
      self.register_buffer('alphas_cumprod_prev', to_torch(alphas_cumprod_prev))

# calculations for diffusion q(x_t | x_{t-1}) and others
   # 计算 \sqrt{\bar\alpha_t}: 
   self.register_buffer('sqrt_alphas_cumprod', to_torch(np.sqrt(alphas_cumprod)))
   # 计算 \sqrt{(1-\bar\alpha_t)}:
   self.register_buffer('sqrt_one_minus_alphas_cumprod', to_torch(np.sqrt(1. - alphas_cumprod)))
   # 计算 \log{(1-\bar\alpha_t)}:
   self.register_buffer('log_one_minus_alphas_cumprod', to_torch(np.log(1. - alphas_cumprod)))
   # 计算 \sqrt{\frac{1}{\bar\alpha_t}}:
   self.register_buffer('sqrt_recip_alphas_cumprod', to_torch(np.sqrt(1. / alphas_cumprod)))
   # 计算 \sqrt{\frac{1}{\bar\alpha_t} - 1}:
   self.register_buffer('sqrt_recipm1_alphas_cumprod', to_torch(np.sqrt(1. / alphas_cumprod - 1)))

   # calculations for posterior q(x_{t-1} | x_t, x_0)
   posterior_variance = (1 - self.v_posterior) * betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) + self.v_posterior * betas
   # above: equal to 1. / (1. / (1. - alpha_cumprod_tm1) + alpha_t / beta_t)
   self.register_buffer('posterior_variance', to_torch(posterior_variance))
   # below: log calculation clipped because the posterior variance is 0 at the beginning of the diffusion chain
   self.register_buffer('posterior_log_variance_clipped', to_torch(np.log(np.maximum(posterior_variance, 1e-20))))
   self.register_buffer('posterior_mean_coef1', to_torch(
       betas * np.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod)))
   self.register_buffer('posterior_mean_coef2', to_torch(
       (1. - alphas_cumprod_prev) * np.sqrt(alphas) / (1. - alphas_cumprod)))

# 计算 VLB Loss 的系数权重
   if self.parameterization == "eps":
       lvlb_weights = self.betas ** 2 / (
                  2 * self.posterior_variance * to_torch(alphas) * (1 - self.alphas_cumprod))
   elif self.parameterization == "x0":
       lvlb_weights = 0.5 * np.sqrt(torch.Tensor(alphas_cumprod)) / (2. * 1 - torch.Tensor(alphas_cumprod))
   else:
       raise NotImplementedError("mu not supported")
   # TODO how to choose this term
   lvlb_weights[0] = lvlb_weights[1]
   self.register_buffer('lvlb_weights', lvlb_weights, persistent=False)
   assert not torch.isnan(self.lvlb_weights).all()
make_beta_schedule

make_beta_schedule 函数定义在 DDPM Class 外，用于预先生成一组β\beta ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def make_beta_schedule(schedule, n_timestep, linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):
    if schedule == "linear":
        betas = (
                torch.linspace(linear_start ** 0.5, linear_end ** 0.5, n_timestep, dtype=torch.float64) ** 2
        )

    elif schedule == "cosine":
        timesteps = (
                torch.arange(n_timestep + 1, dtype=torch.float64) / n_timestep + cosine_s
        )
        alphas = timesteps / (1 + cosine_s) * np.pi / 2
        alphas = torch.cos(alphas).pow(2)
        alphas = alphas / alphas[0]
        betas = 1 - alphas[1:] / alphas[:-1]
        betas = np.clip(betas, a_min=0, a_max=0.999)

    elif schedule == "sqrt_linear":
        betas = torch.linspace(linear_start, linear_end, n_timestep, dtype=torch.float64)
    elif schedule == "sqrt":
        betas = torch.linspace(linear_start, linear_end, n_timestep, dtype=torch.float64) ** 0.5
    else:
        raise ValueError(f"schedule '{schedule}' unknown.")
    return betas.numpy()

前向加噪过程

  • 计算q(xt∣x0)=N(xt;αˉtx0,(1−αˉt)I)q(\mathbf{x}_t \vert \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) 和 一步扩散到xt\mathbf x_t：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def q_mean_variance(self, x_start, t):
    """
    Get the distribution q(x_t | x_0).
    :param x_start: the [N x C x ...] tensor of noiseless inputs.
    :param t: the number of diffusion steps (minus 1). Here, 0 means one step.
    :return: A tuple (mean, variance, log_variance), all of x_start's shape.
    """
    mean = (extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start)
    variance = extract_into_tensor(1.0 - self.alphas_cumprod, t, x_start.shape)
    log_variance = extract_into_tensor(self.log_one_minus_alphas_cumprod, t, x_start.shape)
    return mean, variance, log_variance

def q_sample(self, x_start, t, noise=None):
    noise = torch.randn_like(x_start) if noise is None else noise
    return (extract_into_tensor(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
            extract_into_tensor(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise)
  • 给定噪声反过来计算x0=1αˉt  xt−1αˉt−1  ϵt(⋆)\mathbf{x}_0=\sqrt{\frac1{\bar{\alpha}_t}}\;\mathbf{x}_t-\sqrt{\frac1{\bar{\alpha}_t}-1}\;\boldsymbol{\epsilon}_t\quad(\star)
1
2
3
4
5
def predict_start_from_noise(self, x_t, t, noise):
    return (
            extract_into_tensor(self.sqrt_recip_alphas_cumprod, t, x_t.shape) * x_t -
            extract_into_tensor(self.sqrt_recipm1_alphas_cumprod, t, x_t.shape) * noise
    )
  • 计算带x0\mathbf x_0 的条件后验分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0)
1
2
3
4
5
6
7
8
def q_posterior(self, x_start, x_t, t):
    posterior_mean = (
            extract_into_tensor(self.posterior_mean_coef1, t, x_t.shape) * x_start +
            extract_into_tensor(self.posterior_mean_coef2, t, x_t.shape) * x_t
    )
    posterior_variance = extract_into_tensor(self.posterior_variance, t, x_t.shape)
    posterior_log_variance_clipped = extract_into_tensor(self.posterior_log_variance_clipped, t, x_t.shape)
    return posterior_mean, posterior_variance, posterior_log_variance_clipped
extract_into_tensor

其中函数 extract_into_tensor(a, t, x_shape) 定义在 Class 外，表示从数组 a 中拿取第 t 个元素, 并 reshape 为兼容 x_shape 的形状的 torch.tensor 对象.

1
2
3
4
def extract_into_tensor(a, t, x_shape):
    b, *_ = t.shape
    out = a.gather(-1, t)
    return out.reshape(b, *((1,) * (len(x_shape) - 1)))

反向去噪过程

  • 将 (★) 式中的ϵt\boldsymbol\epsilon_t 用 UNet（self.model）预测，然后代入到条件后验分布q(xt−1∣xt,x0)q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) （self.q_posterior）中，得到pθ(xt−1∣xt)p_\theta(\mathbf{x}_{t-1} \vert \mathbf{x}_t)：
1
2
3
4
5
6
7
8
9
10
11
def p_mean_variance(self, x, t, clip_denoised: bool):
    model_out = self.model(x, t)
    if self.parameterization == "eps":
        x_recon = self.predict_start_from_noise(x, t=t, noise=model_out)
    elif self.parameterization == "x0":
        x_recon = model_out
    if clip_denoised:
        x_recon.clamp_(-1., 1.)

    model_mean, posterior_variance, posterior_log_variance = self.q_posterior(x_start=x_recon, x_t=x, t=t)
    return model_mean, posterior_variance, posterior_log_variance
  • 单步采样和TT步采样生成重构图（无梯度）：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
  @torch.no_grad()
  def p_sample(self, x, t, clip_denoised=True, repeat_noise=False):
      b, *_, device = *x.shape, x.device
      model_mean, _, model_log_variance = self.p_mean_variance(x=x, t=t, clip_denoised=clip_denoised)
      
      # 返回一个和x一样形状的标准高斯噪音noise
   # repeat_noise表示是否重复使用一个噪音, 若重复使用, 一个batch内的所有样本将加同一个随机噪音; 否则每个样本将独立采样
      noise = noise_like(x.shape, device, repeat_noise)
      
   # nonzero_mask表示是否有噪音, t=0时无噪音(为0), 其它时候有噪音(为1)
# no noise when t == 0
      nonzero_mask = (1 - (t == 0).float()).reshape(b, *((1,) * (len(x.shape) - 1)))
      return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise

  @torch.no_grad()
  def p_sample_loop(self, shape, return_intermediates=False):
      device = self.betas.device
      b = shape[0]
      img = torch.randn(shape, device=device)
      intermediates = [img]
      for i in tqdm(reversed(range(0, self.num_timesteps)), desc='Sampling t', total=self.num_timesteps):
          img = self.p_sample(img, torch.full((b,), i, device=device, dtype=torch.long),
                              clip_denoised=self.clip_denoised)
          if i % self.log_every_t == 0 or i == self.num_timesteps - 1:
              intermediates.append(img) # 存中间的图像
      if return_intermediates:
          return img, intermediates
      return img

  @torch.no_grad()
  def sample(self, batch_size=16, return_intermediates=False):
      image_size = self.image_size
      channels = self.channels
      return self.p_sample_loop((batch_size, channels, image_size, image_size), return_intermediates=return_intermediates)
noise_like

其中函数 noise_like(shape, device, repeat=False) 定义在 Class 外，返回一个和 x 一样形状的标准高斯噪音 noise：

1
2
3
4
def noise_like(shape, device, repeat=False):
    repeat_noise = lambda: torch.randn((1, *shape[1:]), device=device).repeat(shape[0], *((1,) * (len(shape) - 1)))
    noise = lambda: torch.randn(shape, device=device)
    return repeat_noise() if repeat else noise()

损失函数计算

给定时间步tt和噪声ϵt\boldsymbol\epsilon_t，先一次性从x0\mathbf x_0 扩散到xt\mathbf x_t （self.q_sample），然后输入xt\mathbf x_t 和tt （带条件生成式还需传入条件cc）调用UNet （self.model）预测噪声ϵθ\boldsymbol\epsilon_\theta （model_out）。然后计算噪声之间的直接损失（self.get_loss），根据参数调整这个直接的 Simple Loss 和 VLB Loss 的比重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def get_loss(self, pred, target, mean=True):
    if self.loss_type == 'l1':
        loss = (target - pred).abs()
        if mean:
            loss = loss.mean()
    elif self.loss_type == 'l2':
        if mean:
            loss = torch.nn.functional.mse_loss(target, pred)
        else:
            loss = torch.nn.functional.mse_loss(target, pred, reduction='none')
    else:
        raise NotImplementedError("unknown loss type '{loss_type}'")

    return loss

def p_losses(self, x_start, t, noise=None):
    noise = torch.randn_like(x_start) if noise is None else noise
    x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise)
    model_out = self.model(x_noisy, t)

    loss_dict = {}
    if self.parameterization == "eps":
        target = noise
    elif self.parameterization == "x0":
        target = x_start
    else:
        raise NotImplementedError(f"Paramterization {self.parameterization} not yet supported")

    loss = self.get_loss(model_out, target, mean=False).mean(dim=[1, 2, 3])

    log_prefix = 'train' if self.training else 'val'

    loss_dict.update({f'{log_prefix}/loss_simple': loss.mean()})
    loss_simple = loss.mean() * self.l_simple_weight

    loss_vlb = (self.lvlb_weights[t] * loss).mean()
    loss_dict.update({f'{log_prefix}/loss_vlb': loss_vlb})

    loss = loss_simple + self.original_elbo_weight * loss_vlb

    loss_dict.update({f'{log_prefix}/loss': loss})

    return loss, loss_dict

def forward(self, x, *args, **kwargs):
    # b, c, h, w, device, img_size, = *x.shape, x.device, self.image_size
    # assert h == img_size and w == img_size, f'height and width of image must be {img_size}'
    t = torch.randint(0, self.num_timesteps, (x.shape[0],), device=self.device).long()
    return self.p_losses(x, t, *args, **kwargs)

训练验证步

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
   def get_input(self, batch):
       x = batch
       # 处理输入图像是灰度图的情况
       if len(x.shape) == 3:
           x = x[..., None]
       x = rearrange(x, 'b h w c -> b c h w')
       x = x.to(memory_format=torch.contiguous_format).float()
       return x

   def shared_step(self, batch):
       x = self.get_input(batch)
       loss, loss_dict = self(x)
       return loss, loss_dict

   def training_step(self, batch, batch_idx):
       loss, loss_dict = self.shared_step(batch)

       self.log_dict(loss_dict, prog_bar=True,
                     logger=True, on_step=True, on_epoch=True)

       self.log("global_step", self.global_step,
                prog_bar=True, logger=True, on_step=True, on_epoch=False)

       if self.use_scheduler:
           lr = self.optimizers().param_groups[0]['lr']
           self.log('lr_abs', lr, prog_bar=True, logger=True, on_step=True, on_epoch=False)

       return loss

   @torch.no_grad()
   def validation_step(self, batch, batch_idx):
       _, loss_dict_no_ema = self.shared_step(batch)
       self.log_dict(loss_dict_no_ema, prog_bar=False, logger=True, on_step=False, on_epoch=True)

def configure_optimizers(self):
       lr = self.learning_rate
       params = list(self.model.parameters())
       if self.learn_logvar:
           params = params + [self.logvar]
       opt = torch.optim.AdamW(params, lr=lr)
       return opt

条件生成

构造函数

  • CondDiffusion 继承 DDPM 类，扩充实现了条件生成部分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
class CondDiffusion(DDPM):
    def __init__(self,
                 first_stage_model, # For LDM
                 cond_stage_model,
                 num_timesteps_cond=None,
                 cond_stage_trainable=False,
                 concat_mode=True,
                 conditioning_key=None,
                 *args, **kwargs):

		# 条件加入的时间步
        self.num_timesteps_cond = num_timesteps_cond if num_timesteps_cond is not None else 1
        assert self.num_timesteps_cond <= kwargs['timesteps']
        
        # for backwards compatibility after implementation of DiffusionWrapper
        if conditioning_key is None:
            conditioning_key = 'concat' if concat_mode else 'crossattn'
		
		ckpt_path = kwargs.pop("ckpt_path", None)
        ignore_keys = kwargs.pop("ignore_keys", [])

        super().__init__(conditioning_key=conditioning_key, *args, **kwargs)

		# 额外加入了条件编码和隐变量编码，适配LDM
		# 条件编码是否可训练
        if cond_stage_trainable:
            self.cond_stage_model = cond_stage_model.train()
        else:
            self.cond_stage_model = cond_stage_model.eval()
            for param in self.first_stage_model.parameters():
                param.requires_grad = False

		# 通常LDM第一阶段训练完毕后冻结参数
        self.first_stage_model = first_stage_model.eval()
        for param in self.first_stage_model.parameters():
            param.requires_grad = False

        self.restarted_from_ckpt = False
        if ckpt_path is not None:
            self.init_from_ckpt(ckpt_path, ignore_keys)
            self.restarted_from_ckpt = True

注册条件时间表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
   def make_cond_schedule(self, ):
       self.cond_ids = torch.full(size=(self.num_timesteps,), fill_value=self.num_timesteps - 1, dtype=torch.long)
       ids = torch.round(torch.linspace(0, self.num_timesteps - 1, self.num_timesteps_cond)).long()
       self.cond_ids[:self.num_timesteps_cond] = ids

# 重构注册时间表的函数
   def register_schedule(self,
                         given_betas=None, beta_schedule="linear", timesteps=1000,
                         linear_start=1e-4, linear_end=2e-2, cosine_s=8e-3):
       # 继承父类的注册方法
       super().register_schedule(given_betas, beta_schedule, timesteps, linear_start, linear_end, cosine_s)

       self.shorten_cond_schedule = self.num_timesteps_cond > 1
       if self.shorten_cond_schedule:
           self.make_cond_schedule()

训练步重构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
  def shared_step(self, batch, **kwargs):
      x, c = batch
      x = self.encode_first_stage(x) # 自定义
      c = self.encode_cond_stage(c) # 自定义
      loss = self(x, c)
      return loss

  def forward(self, x, c, *args, **kwargs):
      t = torch.randint(0, self.num_timesteps, (x.shape[0],), device=self.device).long()
      if self.model.conditioning_key is not None:
          assert c is not None
          # 为条件也施加扩散过程
          if self.shorten_cond_schedule:  # TODO: drop this option
              tc = self.cond_ids[t].to(self.device)
              c = self.q_sample(x_start=c, t=tc, noise=torch.randn_like(c.float()))
      return self.p_losses(x, c, t, *args, **kwargs)


  def p_losses(self, x_start, cond, t, noise=None):
      noise = torch.randn_like(x_start) if noise is None else noise
      x_noisy = self.q_sample(x_start=x_start, t=t, noise=noise)
      # 通过 apply_model 重定义如何用模型结合条件预测噪声
      model_output = self.apply_model(x_noisy, t, cond)

      loss_dict = {}
      prefix = 'train' if self.training else 'val'

      if self.parameterization == "x0":
          target = x_start
      elif self.parameterization == "eps":
          target = noise
      else:
          raise NotImplementedError()

      loss_simple = self.get_loss(model_output, target, mean=False).mean([1, 2, 3])
      loss_dict.update({f'{prefix}/loss_simple': loss_simple.mean()})

# 用可学习参数动态调整损失配比
      logvar_t = self.logvar[t].to(self.device)
      loss = loss_simple / torch.exp(logvar_t) + logvar_t
      if self.learn_logvar:
          loss_dict.update({f'{prefix}/loss_gamma': loss.mean()})
          loss_dict.update({'logvar': self.logvar.data.mean()})

      loss = self.l_simple_weight * loss.mean()

      loss_vlb = self.get_loss(model_output, target, mean=False).mean(dim=(1, 2, 3))
      loss_vlb = (self.lvlb_weights[t] * loss_vlb).mean()
      loss_dict.update({f'{prefix}/loss_vlb': loss_vlb})
      loss += (self.original_elbo_weight * loss_vlb)
      loss_dict.update({f'{prefix}/loss': loss})

      return loss, loss_dict


  def configure_optimizers(self):
      lr = self.learning_rate
      params = list(self.model.parameters())
      if self.cond_stage_trainable:
          print(f"{self.__class__.__name__}: Also optimizing conditioner params!")
          params = params + list(self.cond_stage_model.parameters())
      if self.learn_logvar:
          print('Diffusion model optimizing logvar')
          params.append(self.logvar)
      opt = torch.optim.AdamW(params, lr=lr)
      return opt

采样生成重构

除了增加条件的时间表以外，增加了更多额外的可选项和验证，比如 对噪声 dropout 、对图像 mask、是否 callback 和存储中间过程 intermediates 等。此外还支持了采样加速 ddim，具体实现见下一节。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
@torch.no_grad()
def p_sample(self, x, c, t, clip_denoised=False, repeat_noise=False, return_x0=False,
             temperature=1., noise_dropout=0.):
    b, *_, device = *x.shape, x.device
    outputs = self.p_mean_variance(x=x, c=c, t=t, clip_denoised=clip_denoised,
                                   return_x0=return_x0)
    if return_x0:
        model_mean, _, model_log_variance, x0 = outputs
    else:
        model_mean, _, model_log_variance = outputs

    noise = noise_like(x.shape, device, repeat_noise) * temperature
    
    # 新增了对噪声的dropout
    if noise_dropout > 0.:
        noise = torch.nn.functional.dropout(noise, p=noise_dropout)
    # no noise when t == 0
    nonzero_mask = (1 - (t == 0).float()).reshape(b, *((1,) * (len(x.shape) - 1)))

    if return_x0:
        return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise, x0
    else:
        return model_mean + nonzero_mask * (0.5 * model_log_variance).exp() * noise

@torch.no_grad()
def p_sample_loop(self, cond, shape, return_intermediates=False,
                  x_T=None, verbose=True, callback=None, timesteps=None,
                  mask=None, x0=None, img_callback=None, start_T=None,
                  log_every_t=None):

    if not log_every_t:
        log_every_t = self.log_every_t
    device = self.betas.device
    b = shape[0]
    if x_T is None:
        img = torch.randn(shape, device=device)
    else:
        img = x_T

    intermediates = [img]
    if timesteps is None:
        timesteps = self.num_timesteps

    if start_T is not None:
        timesteps = min(timesteps, start_T)
    iterator = tqdm(reversed(range(0, timesteps)), desc='Sampling t', total=timesteps) if verbose else reversed(
        range(0, timesteps))

    if mask is not None:
        assert x0 is not None
        assert x0.shape[2:3] == mask.shape[2:3]  # spatial size has to match

    for i in iterator:
        ts = torch.full((b,), i, device=device, dtype=torch.long)
        if self.shorten_cond_schedule:
            assert self.model.conditioning_key != 'hybrid'
            tc = self.cond_ids[ts].to(cond.device)
            cond = self.q_sample(x_start=cond, t=tc, noise=torch.randn_like(cond))

        img = self.p_sample(img, cond, ts,
                            clip_denoised=self.clip_denoised)
        if mask is not None:
            img_orig = self.q_sample(x0, ts)
            img = img_orig * mask + (1. - mask) * img

        if i % log_every_t == 0 or i == timesteps - 1:
            intermediates.append(img)
        if callback: callback(i)
        if img_callback: img_callback(img, i)

    if return_intermediates:
        return img, intermediates
    return img

@torch.no_grad()
def sample(self, cond, batch_size=16, return_intermediates=False, x_T=None,
           verbose=True, timesteps=None, mask=None, x0=None, shape=None,**kwargs):
    if shape is None:
        shape = (batch_size, self.channels, self.image_size, self.image_size)
    return self.p_sample_loop(cond,
                              shape,
                              return_intermediates=return_intermediates, x_T=x_T,
                              verbose=verbose, timesteps=timesteps,
                              mask=mask, x0=x0)

@torch.no_grad()
def sample_log(self, cond, batch_size, ddim, ddim_steps, **kwargs):

    if ddim:
        ddim_sampler = DDIMSampler(self)
        shape = (self.channels, self.image_size, self.image_size)
        samples, intermediates =ddim_sampler.sample(ddim_steps,batch_size,
                                                    shape,cond,verbose=False,**kwargs)

    else:
        samples, intermediates = self.sample(cond=cond, batch_size=batch_size,
                                             return_intermediates=True,**kwargs)

    return samples, intermediates

DDIM加速

离散扩散 (D3PM)

VQ-VAE

VQ-VAE的作者认为，VAE的生成图片之所以质量不高，是因为图片被编码成了连续向量。而实际上，把图片编码成离散向量会更加自然。比如我们想让画家画一个人，我们会说这个是男是女，年龄是偏老还是偏年轻，体型是胖还是壮，而不会说这个人性别是0.5，年龄是0.6，体型是0.7。因此，VQ-VAE会把图片编码成离散向量，如下图所示。

VQ-VAE使用了一种叫做"straight-through estimator"的技术来完成梯度复制。这种技术是说，前向传播和反向传播的计算可以不对应。你可以为一个运算随意设计求梯度的方法。基于这一技术，VQ-VAE使用了一种叫做sg(stop gradient，停止梯度)的运算。

其实就是 ().detach()

https://zhuanlan.zhihu.com/p/640000410
快速了解矢量量化Vector-Quantized(VQ)及相应代码_vectorquantize代码-CSDN博客
https://blog.csdn.net/shebao3333/article/details/139669554

参考

  1. 轻松理解 VQ-VAE：首个提出 codebook 机制的生成模型 - 知乎
  2. 快速了解矢量量化Vector-Quantized(VQ)及相应代码_vectorquantize代码-CSDN博客
  3. What are Diffusion Models? | Lil’Log
  4. 人工智能 - 扩散模型(Diffusion Model)详解：直观理解、数学原理、PyTorch 实现 - 个人文章 - SegmentFault 思否
  5. 由浅入深了解Diffusion Model - 知乎
  6. 生成扩散模型漫谈（一）：DDPM = 拆楼 + 建楼 - 科学空间|Scientific Spaces
  7. 扩散模型（Diffusion Model）原理及代码实现-微信公众平台
  8. 扩散概率模型（diffusion probabilistic models） — 张振虎的博客 张振虎 文档
  9. 关于 DDIM 采样算法的推导 | Ze’s Blog
  10. 一文读懂DDIM凭什么可以加速DDPM的采样效率 - 知乎
  11. 生成扩散模型漫谈（四）：DDIM = 高观点DDPM - 科学空间|Scientific Spaces
  12. diffusion model(二)：DDIM技术小结 (denoising diffusion implicit model) | 莫叶何竹🍀
  13. 笔记｜扩散模型（二）：DDIM 理论与实现 | 極東晝寢愛好家
  14. 笔记｜扩散模型（四）：Classifier Guidance 理论与实现 | 極東晝寢愛好家
  15. 笔记｜扩散模型（七）：Latent Diffusion Models（Stable Diffusion）理论与实现 | 極東晝寢愛好家
  16. 生成扩散模型漫谈（九）：条件控制生成结果 - 科学空间|Scientific Spaces
  17. Latent Diffusion Models (LDMs) 模型学习笔记-CSDN博客
  18. DIFFUSION 系列笔记| Latent Diffusion Model | 记忆笔书
  19. 一文详解 Latent Diffusion官方源码_diagonalgaussiandistribution-CSDN博客