机器学习那些杂乱无章的小知识

分类和回归的区别是什么？

• 分类（ classification ）是对输入（input） 进行类别上的预测（ prediction ） 和指派
• 回归（ regression ）是找出输入与输出的关系映射，并对输入做出数值上的输出预测

分类和输出均属于 监督学习问题（ supervised learning ），其任务是学习从输入$X$到输出$Y$的映射：

$$f:X\to Y,X\in A,Y\in B$$

关于二者的区别，可以从以下几个方面进行总结：

1. 目的不同：分类主要是为了对数据集中的数据进行类型甄别，在二分类中就是为了寻找决策边界；而回归则偏向于对值的预测，通过找寻最优拟合从而使得预测值接近真实值。
2. 输出不同：分类输出的值是离散的，回归输出的值是连续的。
3. 评估不同：分类利用混淆矩阵、准确率等方式进行评估；回归则是使用SSE、拟合优度等。

参考：1.知乎问答、2.CSDN文章

VC维是什么？

待更

输入变量的特征既包含有离散值和连续值时应该如何选择回归模型？

2021.10.31更新：选择的回归模型应该是更加通用的：广义线性回归模型

首先是对于“离散值”的定义，这里的离散值指的是分类值，例如一个员工的性别特征只有男和女（可以用1和0进行映射）。

对于上述离散特征的定义/编码，又分两种情况：

1. 离散特征的取值之间没有大小的意义，比如$color:[red,blue]$,那么就使用one-hot编码
2. 离散特征的取值有大小的意义，比如$size:[X,XL,XXL]$,那么就使用数值的映射$\{X:1,XL:2,XXL:3\}$

由于对模型进行评估和损失函数计算时，常常涉及的是连续值，并且需要通过值与值之间的距离进行测定，所以对于上述情况中的第一种情况，单纯的对颜色特征进行标号，会出现问题，所以需要引入 one-hot | 独热编码 对此类离散值进行编码，从而便于机器学习的读取和利用。

对于每一个特征，如果它有$m$ 个可能值，那么经过独热编码后，就变成了$m$ 个二元特征。
例如：成绩这个特征有 （好，中，差），变成one-hot就是 100, 010, 001 。并且，这些特征互斥，每次只有一个激活。因此，数据会变成稀疏的。

独热编码的优点：

1. 解决了分类器不好处理属性数据的问题
2. 在一定程度上也起到了扩充特征的作用

独热编码的缺点：

1. 难以处理利用文本特征的这类词袋模型，不考虑词与词之间的顺序（文本中词的顺序信息也是很重要的）；
2. 其次，它假设词与词相互独立（在大多数情况下，词与词是相互影响的）；
3. 最后，它得到的特征是离散稀疏的。

参考：1.独热编码（One-Hot）及其代码、2.One-Hot 和 LabelEncoder标签编码

训练集、验证集、测试集各自的作用是什么？

在有监督的机器学习模型的训练中，一般会将原始数据划分三个部分，即训练集（train set），验证集（validation set），测试集（test set）。

其中，三个数据集的作用如下：

• 训练集：用作模型拟合的数据样本
• 验证集：评估模型预测的好坏及调整对应的参数
• 测试集：用来评估模最终模型的泛化能力

参考：1.小专栏、2.CSDN文章

如何检验数据的正态性？

在MTALAB中，正态分布的检验方法有如下几种：

• $chi2gof$ |卡方检验，适合大样本，一般要求50个以上
• $kstest$ |Kolmogorov-Smirnov检验，适于小样本
• $lillietest$ |Lilliefors检验，用于正态分布，与kstest类似，适用于小样本
• $jbtest$ |Jarque-Bera检验，是通过峰度、偏度检测正态分布的，适用用大样本

此处以data数据为例分别进行验证：

close all;clear;clc;
% 测试数据
data = [2.90800803072936 0.825218894228491 1.37897197791661 -1.05818025798736 -0.468615581100624 -0.272469409250188 1.09842461788862 -0.277871932787639 0.701541458163284 -2.05181629991115 -0.353849997774433 -0.823586525156853 -1.57705702279920 0.507974650905946 0.281984063670556 0.0334798822444514 -1.33367794342811 1.12749227834159 0.350179410603312 -0.299066030332982 0.0228897927516298 -0.261995434966092 -1.75021236844679 -0.285650971595330 -0.831366511567624 -0.979206305167302 -1.15640165566400 -0.533557109315987 -2.00263573588306 0.964229422631628]';

%% 卡方检验
[H1,s1,stats]=chi2gof(data);
if H1 == 0
    disp('卡方检验：服从正态分布');
end

%% KS检验
% 正态分布参数估计
[mu,sigma] = normfit(data);
% 根据参数生成正态分布函数
p=normcdf(data,mu,sigma);
% 进行ks检验
[H2,s2]=kstest(data,[data,p],0.05);
if H2==0
    disp('KS检验：服从正态分布');
end

%% Lilliefors检验
[H3,s3]=lillietest(data);
if H3==0
    disp('Lilliefors检验：服从正态分布');
end

%% Jarque-Bera检验
[H4,s4]=jbtest(data,0.05);
if H4==0
    disp('Jarque-Bera检验：服从正态分布');
end

$Output$:（默认$α=0.05$）

卡方检验：服从正态分布
KS检验：服从正态分布
Lilliefors检验：服从正态分布
Jarque-Bera检验：服从正态分布

参考：Matlab正态分布检验

什么是马氏距离，如何计算？

马氏距离（Mahalanobis Distance）是由马哈拉诺比斯（P. C. Mahalanobis）提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。

一般来说，马氏距离排除了量纲的影响，具有尺度无关性，即与数据的测量单位无关；同时也排除了特征之间相关性的干扰。

下面给出样本集$A$中一点$P$（坐标为$\mathbf{x}$）到样本集$B$中心$O$（坐标为$\mathbf{μ}$）的马氏距离$D_M(\mathbf{x})$：

$$D_M(x) = \sqrt{(x-\mu)^T {S}^{-1}(x-\mu)}$$

其中，$S$是样本集$B$的协方差矩阵。

下面以一个简单的实例进行计算：

某二维分布，中心点在$[2,3]$，协方差矩阵为$\begin{bmatrix}1, 0\\0, 2\end{bmatrix}$试计算$[10,10]$点与中心点的欧氏距离和马氏距离。

有：欧氏距离$d=\sqrt{(2-10)^2+(3-10)^2}=10.63$

欧氏距离$d_M=\sqrt{\frac 1 2[10-2,10-3]\begin{bmatrix}2, 0\\0, 1\end{bmatrix}\begin{bmatrix}10-2\\10-3\end{bmatrix}}=9.41$

参考：马氏距离和欧式距离详解|CSDN、《机器学习导论》中文版56页

什么是范数？有什么性质？

待更，见动手学深度学习

何为公共协方差，有什么用？

根据公共协方差的定义，有：

$$\mathbf{S}=\sum_i \hat{P}(C_i)\mathbf{S}_i$$

其中，$\hat{P}(C_i)=\frac{\sum_tr_i^t}{N}$，如果第$t$个样本$\mathbf{x}^t\in C_i$，则$r_i^t=1$，否则为$0$。

待更

MSE与偏倚和方差？

自创理解之蓝色散点与红色散点

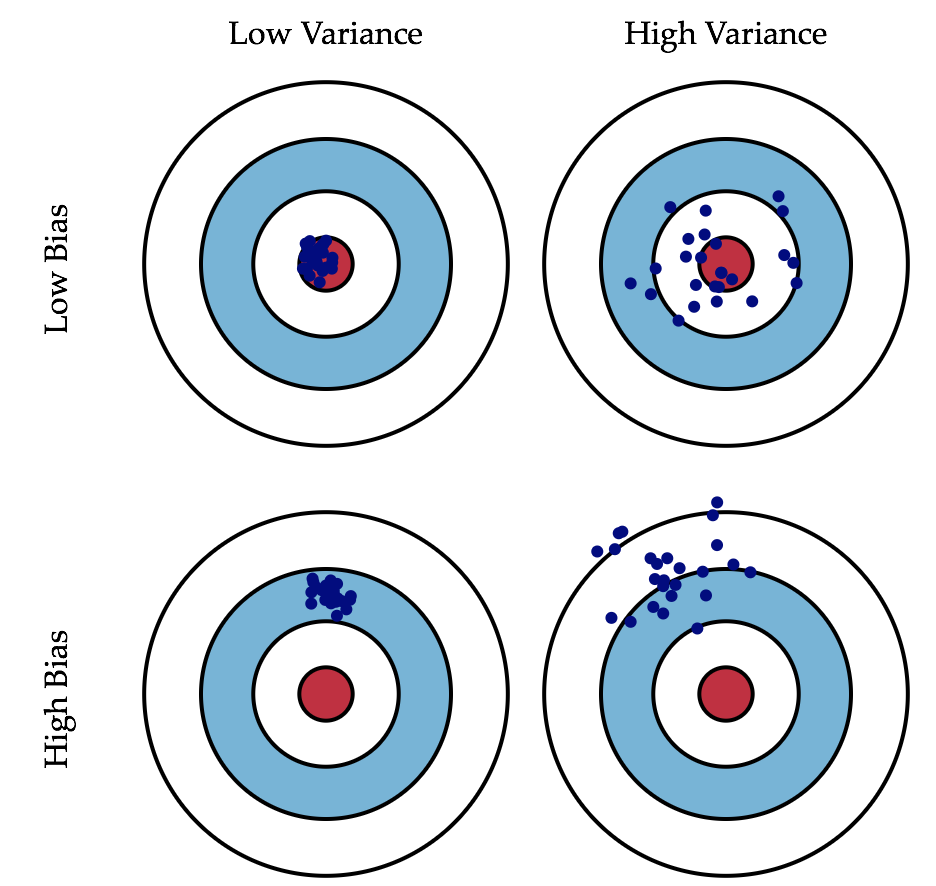
https://blog.csdn.net/Just_do_myself/article/details/103357618

公式上的理解：

$$MSE(\hat\theta)=\Bbb E\left[(\hat\theta-\Bbb E[\hat\theta])^2\right]+\left(\Bbb E[\hat\theta]-\theta_o\right)^2$$

什么是Feature Embedding|_特征嵌入？

什么是Manifold|_流形？

“流形”这个中文词|_翻译 取自文天祥的“天地有正气，杂然赋流形”

这个词第一次作为当前的数学意义使用是由北大数学系的一位老教授江泽涵 老先生

老先生是我国代数拓扑学的开拓者

参考：浅谈流形学习

深度学习中的Linear、Dense、MLP、FC有什么区别？

$\textbf{Linear}$：线性层，最原始的称谓，单层即无隐层。torch中的 torch.nn.Linear就是提供了一个 in_dim * out_dim 的 tensor layer。

$\textbf{Dense}$：密集层，可以指单层 linear 也可以指多层堆叠，有无隐层均可，但一般多指有隐层。keras中常常提到的 dense 层其实就是多层线性层的堆叠。

$\textbf{MLP}$：多层感知器（Multi-layer Perceptron Neural Networks），指多层 linear 的堆叠，有隐层。

$\textbf{FC}$：全连接层（Fully Connected Layer），单层多层均可以表示，是对 Linear Classifier最笼统的一种称谓。

参考：# 深度学习Linear,Dense,MLP,FC区别是啥？

什么是超参数？和参数有什么区别？

机器学习模型中一般有两类参数：

一类需要从数据中学习和估计得到，称为模型参数（Parameter）—即模型本身的参数。比如，线性回归直线的加权系数（斜率）及其偏差项（截距）都是模型参数。

还有一类则是机器学习算法中的调优参数（tuning parameters），需要人为设定，称为超参数（Hyperparameter）。比如，迭代次数、学习率、退化率、正则化系数λ、决策树模型中树的深度等。

机器学习中一直说的“调参”，实际上不是调“参数”，而是调“超参数”。

参考：超参数（Hyperparameter） - HuZihu

如何进行网格搜索来调参？

GridSearchCV
https://zhuanlan.zhihu.com/p/642060346
https://blog.csdn.net/Roy_Allen/article/details/131030684

什么是Ablation Study (消融实验）？

消融 的原意是通过手术切除身体组织。

消融研究 |Ablation study 一词起源于 20 世纪 60 年代和 70 年代的实验神经心理学领域，通过切除部分动物大脑来研究这对动物行为的影响。

在机器学习领域，尤其是复杂的深度神经网络中，消融实验被用来描述切除网络某些部分的过程，以便更好地了解网络的行为，探寻因果关系。

可以看出，消融实验的目的在于移除系统中的特定的部分，来控制变量式的研究这个部分对于系统整体的影响。
如果去除这一部分后系统的性能没有太大损失，那么说明这一部分对于整个系统而言并不具有太大的重要性；
如果去除之后系统性能明显的下降，则说明这一部分的设计是必不可少的。

当然，如果出现了第三种情况，也就是去除之后模型的性能不降反升，那么建议找一下bug或者修改设计。

	metric 1	…	metric N
A (baseline)
A+B
A+C
A+B+C (final)

举个栗子。在上图中，metric 1 - N 表示N个用来评价系统性能的指标，原始模型 M（只含有 A 模块）会被首先测试，得到的结果会成为baseline用来对比。接下来，分别测试模型 A+B 与 A+C 来分别测试 B 模块与 C 模块的单独作用。最后，就要把所有的模块都放在一起，也就是模型A+B+C，来测试最终模型的性能。

参考：一文搞懂什么是ablation study消融实验|知乎

计算图、静态图和动态图是什么？

计算图是用来描述运算的有向无环图，有两个主要元素：节点 (Node) 和 边 (Edge)。
节点表示数据，如向量、矩阵、标量等；
边表示运算，如加减乘除卷积等。

PyTorch 采用的是动态图机制 (Dynamic Computational Graph)，而 Tensorflow 采用的是静态图机制 (Static Computational Graph)。

动态图 是指计算图的运算和搭建同时进行，也就是可以先计算前面的节点的值，再根据这些值搭建后面的计算图。

优点是灵活，易调节，易调试。PyTorch 里的很多写法跟其他 Python 库的代码的使用方法是完全一致的，没有任何额外的学习成本。

静态图 是先搭建图，然后再输入数据进行运算。

优点是高效，因为静态计算是通过先定义后运行的方式，之后再次运行的时候就不再需要重新构建计算图，所以速度会比动态图更快。

缺点是不灵活。TensorFlow 每次运行的时候图都是一样的，是不能够改变的，所以不能直接使用 Python 的 while 循环语句，需要使用辅助函数 tf.while_loop 写成 TensorFlow 内部的形式。

参考：计算图与动态图和静态图机制 - 知乎

二值向量的相似性如何度量？

简单匹配系数 SMC

Jaccard系数

类别与类别的相关性用卡方（？）

softmax函数？

pytorch | softmax(x,dim=-1)参数dim的理解 - 知乎 (zhihu.com)

Zipf分布？

Zipf 定律(齐普夫定律，Zipf’s law) 是美国语言学家 George K. Zipf 发现的，他在1932年研究英文单词的出现频率时，发现如果把单词频率从高到低的次序排列，每个单词出现频率$n_i$ 和它的符号访问排名$i$ 存在简单反比关系：

$$n_i\propto\frac1{i^\alpha}$$

等价于：

$$\log n_i=-\alpha\log i+c$$

对词频分布来说：$\alpha$ 取1，$c$ 取0.01。

一个样本数为$n$ 的离散随机变量的齐普夫分布$X\sim\text{Zipf}(\alpha,n)$，它的概率分布函数(概率质量函数)为：

$$\text{Zipf}(x;\alpha,n)=P(X=x)=\frac1{x^\alpha\sum_{i=1}^n(1/i^\alpha)}$$

当$n\to\infty$ 时，有黎曼函数：

$$\zeta(\alpha)=\sum_{k=1}^\infty\left(\frac1k\right)^\alpha$$

此时齐普夫分布变成了 Zeta 分布；当$\alpha=0$ 时，齐普夫分布变成了均匀分布。

混淆矩阵、召回率、F1Score？

https://zhuanlan.zhihu.com/p/464719532
分类评价指标 F值 详解 | Micro F1 & Macro F1 & Weight F1-CSDN博客

拉普拉斯平滑法？