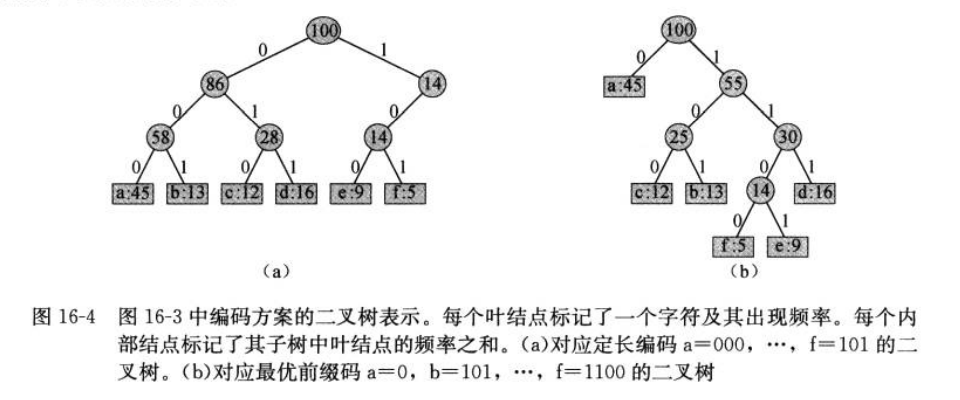
哈夫曼树|Huffman Tree 在数据通信中,如果允许对不同的字符采用不等长的二进制码进行表示,那么这种编码方式称为 可变长度编码(variable-length code) 。该编码方式对使用频率较高的字符赋以短编码,从而使得字符的平均编码长度减小,实现了压缩数据的效果。
哈夫曼编码 就是一种被广泛运用的数据压缩编码,通常可以节省 20%~90% 的空间。
如果没有一个编码是另一个编码的前缀,则称这样的编码是 前缀码(prefix code) 。001011101,如果根据前缀码的唯一性(没有二义性)的思路进行解码,那么可以得到0,0,101,1101,这个解码过程是没有歧义的。
前缀码被证明是可以保证达到最优数据压缩率的一种编码,而哈夫曼编码就是基于前缀码实现的。
字符解码 在上面的例子中,我们并没有给出解码的过程。这里再展开阐述。
构造的二叉树应具有如下特点:
叶子结点用于表示所给的的字符; 字符的二进制码通过根结点到对应的叶子结点的路径表示,“0”表示转向左子结点,“1”表示转向右子结点。 注:该二叉树并不是BST,其自己子结点并未有序排列,内部结点也不包含key.
如下图所示,按照这个解码逻辑以及给出的树,我们可以轻松解码刚刚的001011101为aabe。
文件的最优编码方案总是对应一棵 满二叉树 。即任何树内的非叶子结点都有左右两个孩子。
编码与形式化 我们为二叉树定义了一个衡量其是否最优的指标:带权路径长度 。
W P L = ∑ i = 1 n w i l i WPL=\sum_{i=1}^n w_il_i W P L = i = 1 ∑ n w i l i
其中,权 表示的是一棵树中结点被赋予某种意义的数值, 路径长度 是从树根到任意结点经过的边数,而 WPL 就是我们定义的带权路径长度,由叶子结点 与其上的权的乘积组成。w i w_i w i i i i w e i g h t weight w e i g h t l i l_i l i i i i l e n g t h length l e n g t h
如果一棵二叉树使得 WPL 最小,那么这棵树我们就称为 最优二叉树 。
根据前缀码的特点,以及二叉树的特性,我们引入 WPL 就可以得到类似的指标:平均传输位数 。
如果一棵二叉树的平均传输位数最小,那么其对应的编码方式我们就称为 最优前缀码 。
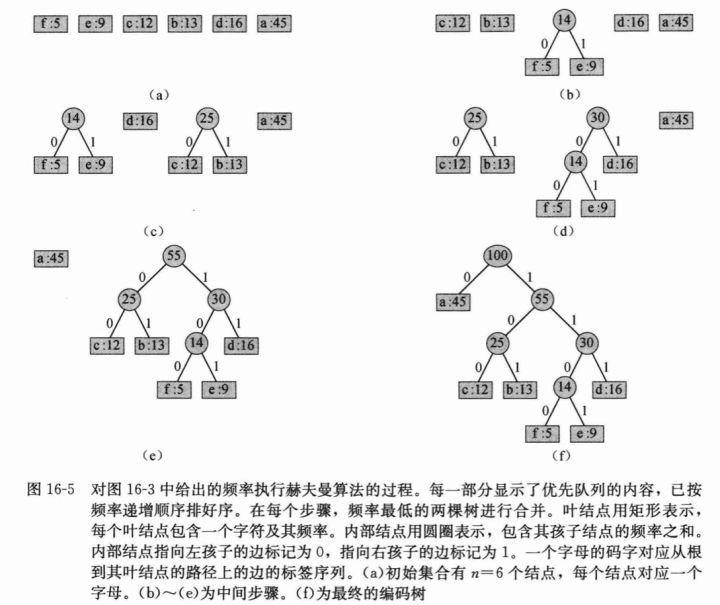
哈夫曼为了构造最优二叉树,利用了贪心算法 的思想。
假定C C C n n n ∀ c ∈ C \forall c\in C ∀ c ∈ C c . f r e q c.freq c . f re q C C C c c c 频率 。
W P L = ∑ c ∈ C c . f r e q × d T ( c ) WPL=\sum_{c\in C}c.freq\times d_T(c) W P L = c ∈ C ∑ c . f re q × d T ( c )
其中,d T ( c ) d_T(c) d T ( c ) c c c T T T
算法伪代码如下:
输入:C = { c 1 , c 2 , . . . , c n } C=\{c_1,c_2,...,c_n\} C = { c 1 , c 2 , ... , c n } 输出:Q Q Q Algorithm: HUFFMAN ( C ) 1. n ← ∣ C ∣ 2. Q ← C / / Q 为按频率 C . f r e q 递增的优先队列 3. f o r i = 1 t o n − 1 d o 4. z ← Allocate-Node ( ) / / 生成一个新结点 z 5. z . l e f t ← x ← Extract-min ( Q ) 6. z . r i g h t ← y ← Extract-min ( Q ) 7. z . f r e q ← x . f r e q + y . f r e q 7. Insert ( Q , z ) 8. r e t u r n Q \begin{aligned} &\text{Algorithm: }\;\text{HUFFMAN}(C)\\\\ 1.&\;n\leftarrow|C|\\ 2.&\;Q\leftarrow C\;//Q\text{为按频率 }C.freq\text{ 递增的优先队列}\\ 3.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;n-1\;\mathbf{do}\\ 4.&\;\qquad z\leftarrow \text{Allocate-Node}()\;//\text{生成一个新结点}z\\ 5.&\;\qquad z.left\leftarrow x\leftarrow\text{Extract-min}(Q)\\ 6.&\;\qquad z.right\leftarrow y\leftarrow\text{Extract-min}(Q)\\ 7.&\;\qquad z.freq\leftarrow x.freq+y.freq\\ 7.&\;\qquad \text{Insert}(Q,z)\\ 8.&\;\mathbf{return}\;Q \end{aligned} 1. 2. 3. 4. 5. 6. 7. 7. 8. Algorithm: HUFFMAN ( C ) n ← ∣ C ∣ Q ← C // Q 为按频率 C . f re q 递增的优先队列 for i = 1 to n − 1 do z ← Allocate-Node ( ) // 生成一个新结点 z z . l e f t ← x ← Extract-min ( Q ) z . r i g h t ← y ← Extract-min ( Q ) z . f re q ← x . f re q + y . f re q Insert ( Q , z ) return Q
哈夫曼树的构造算法 就是:自底向上地,将∣ C ∣ |C| ∣ C ∣ c . f r e q c.freq c . f re q 最小优先队列 Q Q Q ∣ C ∣ − 1 |C|-1 ∣ C ∣ − 1
如果优先队列Q Q Q 最小二叉堆 实现,则每一次循环取出当前最小元的过程需要花费O ( log n ) O(\log n) O ( log n ) O ( n − 1 ) O(n-1) O ( n − 1 ) O ( n ) O(n) O ( n ) O ( n log n ) O(n\log n) O ( n log n ) O ( n ) O(n) O ( n )
正确性证明 哈夫曼树的构造方法被证明完全能得到最优解,即其构造的二叉树的WPL一定最小。因此,我们也把最优二叉树叫做哈夫曼树 。
下面给出其正确性的证明。
因为哈夫曼算法采用的是贪心策略,因此我们要证明其正确性需要从 贪心选择性质 和 最优子结构 两方面进行论证。
贪心选择性质 贪心选择性质 引理1 如果∃ x , y ∈ C \exists x,y \in C ∃ x , y ∈ C x . f r e q x.freq x . f re q y . f r e q y.freq y . f re q C C C x , y x,y x , y
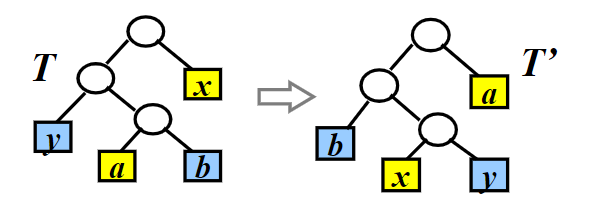
引理1的证明 证明 设T T T C C C a , b a,b a , b T T T a ≠ b a\neq b a = b a . f r e q ≤ b . f r e q & & x . f r e q ≤ y . f r e q a.freq \leq b.freq\;\&\&\; x.freq\leq y.freq a . f re q ≤ b . f re q && x . f re q ≤ y . f re q a , b a,b a , b x , y x,y x , y
x . f r e q ≤ a . f r e q y . f r e q ≤ b . f r e q x.freq \leq a.freq\;\;\;\\y.freq \leq b.freq x . f re q ≤ a . f re q y . f re q ≤ b . f re q
当x . f r e q = b . f r e q x.freq=b.freq x . f re q = b . f re q x . f r e q ≤ y . f r e q x.freq\leq y.freq x . f re q ≤ y . f re q x , b x,b x , b y y y y = b y=b y = b y = x y=x y = x y . f r e q = x . f r e q y.freq=x.freq y . f re q = x . f re q x . f r e q ≤ a . f r e q ≤ b . f r e q = x . f r e q = y . f r e q ⇒ a . f r e q = b . f r e q = x . f r e q = y . f r e q \begin{aligned}x.freq \leq a.freq \leq b.freq =x.freq=y.freq\\\\\Rightarrow a.freq=b.freq=x.freq=y.freq\end{aligned} x . f re q ≤ a . f re q ≤ b . f re q = x . f re q = y . f re q ⇒ a . f re q = b . f re q = x . f re q = y . f re q
这表明,如果将a , b , x , y a,b,x,y a , b , x , y
当x . f r e q ≠ b . f r e q x.freq\neq b.freq x . f re q = b . f re q x ≠ b x\neq b x = b x , a x,a x , a T T T T ′ T' T ′ y , b y,b y , b T ′ T' T ′ T ′ ′ T'' T ′′ x = b , y ≠ a x=b,y\neq a x = b , y = a T ′ ′ T'' T ′′ x , y x,y x , y 于是:
W P L ( T ) − W P L ( T ′ ) = ∑ c ∈ C c . f r e q × d T ( c ) − ∑ c ∈ C c . f r e q × d T ∗ ( c ) = ( a . f r e q − x . f r e q ) [ d T ( a ) − d T ( x ) ] ≥ 0 \begin{aligned}WPL(T)-WPL(T')&=\sum_{c\in C}c.freq\times d_T(c)-\sum_{c\in C}c.freq\times d_{T^*}(c)\\&=(a.freq-x.freq)[d_T(a)-d_T(x)]\\&\geq 0\end{aligned} W P L ( T ) − W P L ( T ′ ) = c ∈ C ∑ c . f re q × d T ( c ) − c ∈ C ∑ c . f re q × d T ∗ ( c ) = ( a . f re q − x . f re q ) [ d T ( a ) − d T ( x )] ≥ 0
类似地,有W P L ( T ′ ) − W P L ( T ′ ′ ) ≥ 0 WPL(T')-WPL(T'')\geq 0 W P L ( T ′ ) − W P L ( T ′′ ) ≥ 0 W P L ( T ) ≥ W P L ( T ′ ′ ) WPL(T)\geq WPL(T'') W P L ( T ) ≥ W P L ( T ′′ ) T ′ ′ T'' T ′′ T T T
最优子结构 最优子结构性质 引理2 令C ′ = ( C − { x , y } ) ∪ z , z . f r e q = x . f r e q + y . f r e q C'=(C-\{x,y\})\cup {z},\quad z.freq=x.freq+y.freq C ′ = ( C − { x , y }) ∪ z , z . f re q = x . f re q + y . f re q T ′ T' T ′ C ′ C' C ′ T ′ T' T ′ z z z x , y x,y x , y T T T C C C
引理2的证明 证明 根据题意,有∀ c ∈ C − { x , y } , d T ( c ) = d T ′ ( c ) \forall c\in C-\{x,y\}, d_T(c)=d_{T'}(c) ∀ c ∈ C − { x , y } , d T ( c ) = d T ′ ( c ) d T ( x ) = d T ( y ) = d T ′ ( x ) + 1 d_T(x)=d_T(y)=d_{T'}(x)+1 d T ( x ) = d T ( y ) = d T ′ ( x ) + 1
W P L ( T ) = W P L ( T ′ ) + x . f r e q + y . f r e q W P L ( T ′ ) = W P L ( T ) − x . f r e q − y . f r e q \begin{aligned}WPL(T)&=WPL(T')+x.freq+y.freq\\WPL(T')&=WPL(T)-x.freq-y.freq\end{aligned} W P L ( T ) W P L ( T ′ ) = W P L ( T ′ ) + x . f re q + y . f re q = W P L ( T ) − x . f re q − y . f re q
利用反证法 。T T T C C C T ∗ T^* T ∗ W P L ( T ∗ ) < W P L ( T ) WPL(T^*)\lt WPL(T) W P L ( T ∗ ) < W P L ( T ) 定理1 可知,T ∗ T^* T ∗ x , y x,y x , y z z z z . f r e q = x . f r e q + y . f r e q z.freq=x.freq+y.freq z . f re q = x . f re q + y . f re q T ∗ ′ T^{*'} T ∗ ′
W P L ( T ∗ ′ ) = W P L ( T ∗ ) − x . f r e q − y . f r e q < W P L ( T ) − x . f r e q − y . f r e q = W P L ( T ′ ) \begin{aligned}WPL(T^{*'})&=WPL(T^*)-x.freq-y.freq\\&\lt WPL(T)-x.freq-y.freq=WPL(T')\end{aligned} W P L ( T ∗ ′ ) = W P L ( T ∗ ) − x . f re q − y . f re q < W P L ( T ) − x . f re q − y . f re q = W P L ( T ′ )
这说明,存在T ∗ ′ T^{*'} T ∗ ′ C ′ C' C ′
哈夫曼算法的正确性 由 引理1 和 引理2 可知,哈夫曼算法能够得到最优解.
编程实现 采用 C++ 语言进行编程,此处利用了 STL 标准库中的优先队列 (头文件<queue>)
因为哈夫曼树是二叉树的一种,因此考虑采用结构体的方式进行存储:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 typedef struct HT { int freq; char key; HT *left; HT *right; }HuffmanTree; struct cmp { bool operator () (HuffmanTree *a, HuffmanTree *b) return a->freq > b->freq; } }; typedef struct { char ch; int freq; }CharSet; typedef priority_queue<HuffmanTree*,vector<HuffmanTree*>,cmp> HTqueue;
然后是根据伪代码实现具体细则:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 void CreateHuffmanTree (HTqueue &Q, CharSet C[], int n) for (int i = 0 ; i < n; i++){ HuffmanTree *tmp = new HuffmanTree (); tmp->key = C[i].ch; tmp->freq = C[i].freq; tmp->left = NULL ; tmp->right = NULL ; Q.push (tmp); } for (int i = 0 ; i < n-1 ; i++){ HuffmanTree *tmp = new HuffmanTree (); HuffmanTree *left = Q.top (); Q.pop (); HuffmanTree *right = Q.top (); Q.pop (); tmp->left = left; tmp->right = right; tmp->freq = left->freq + right->freq; tmp->key = '\0' ; Q.push (tmp); } }
编写函数实现哈夫曼编码:
1 2 3 4 5 6 7 8 9 10 11 void OutputHuffmanCode (HuffmanTree *CodeTree, string code="" ) if (CodeTree->key != '\0' ){ cout << CodeTree->key << ": (" << CodeTree->freq << ")" ; cout << code << endl; } if (CodeTree->left != NULL && CodeTree->right != NULL ){ OutputHuffmanCode (CodeTree->left,code+"0" ); OutputHuffmanCode (CodeTree->right,code+"1" ); } }
实例演示 < a : 45 , b : 13 , c : 12 , d : 16 , e : 9 , f : 5 > <a:45,b:13,c:12,d:16,e:9,f:5> < a : 45 , b : 13 , c : 12 , d : 16 , e : 9 , f : 5 > 100 a: 45 55 25 30 14 c: 12 b: 13 f: 5 e: 9 d: 16 a:0 b:101 c:100 d:111 e:1101 f:1100
下面通过调用算法查看.
主函数:
1 2 3 4 5 6 7 8 int main (void ) HTqueue Q; CharSet C[6 ]={{'a' ,45 },{'b' ,13 },{'c' ,12 },{'d' ,16 },{'e' ,9 },{'f' ,5 }}; CreateHuffmanTree (Q, C, 6 ); OutputHuffmanCode (Q.top ()); cout << "END" << endl; while (1 ); }
输出结果:
1 2 3 4 5 6 7 a: (45)0 c: (12)100 b: (13)101 f: (5)1100 e: (9)1101 d: (16)111 END
Prefect!
最优二叉检索树|Optimal Binary Search Tree 哈夫曼树,也被称作最优二叉树,是通过建立一棵二叉树,对指定频率的字符进行编码,从而使得字符的平均编码长度达到最低,实现了数据的压缩。
而最优二叉检索树则是为了实现对于给定频率的字符,建立BST使得搜索效率最高。
例如想要实现对某英文文本中一个单词的快速查找并翻译,我们可以建立一棵 二叉搜索树 (BST) 存储英文单词,而对于英文中出现频率很高的 the 这一单词,我们希望它在 BST 中更靠近根结点,这样可以很快检索到它。这种使得所有搜索过程中,访问结点个数最少(也就是搜索效率最高)的 BST,就被称为 最优二叉检索树 (OBST)。
形式化表达 给定n n n 已排序 序列K = < k 1 , k 2 , . . . , k n > K=<k_1,k_2,...,k_n> K =< k 1 , k 2 , ... , k n > k 1 < k 2 < ⋯ < k n k_1\lt k_2\lt\cdots\lt k_n k 1 < k 2 < ⋯ < k n k i . p k_i.p k i . p x x x k i k_i k i n + 1 n+1 n + 1 d 0 , d 1 , . . . , d n d_0,d_1,...,d_n d 0 , d 1 , ... , d n K K K 空隙 中,∀ i ≠ 0 , i ≠ n \forall i\neq0,i\neq n ∀ i = 0 , i = n d i d_i d i ( k i , k i + 1 ) (k_i,k_{i+1}) ( k i , k i + 1 ) d 0 : ( − ∞ , k 1 ) , d n : ( k n , + ∞ d_0:(-\infty,k_1),\;d_n:(k_n,+\infty d 0 : ( − ∞ , k 1 ) , d n : ( k n , + ∞ d i . p d_i.p d i . p x x x d i d_i d i
自然有:
∑ i = 1 n k i . p + ∑ i = 0 n d i . p = 1 \sum_{i=1}^nk_i.p+\sum_{i=0}^nd_i.p=1 i = 1 ∑ n k i . p + i = 0 ∑ n d i . p = 1
对上述关键字序列建立任意一棵 BST,显然代表空隙的d i d_i d i 叶子结点 出现。一个示例如下图所示:
通过 BST 搜索某个结点x x x d T ( x ) + 1 d_T(x)+1 d T ( x ) + 1 d T ( x ) d_T(x) d T ( x ) x x x T T T
那么与W P L WPL W P L 期望代价 :
E [ Search cost in T ] = ∑ i = 1 n [ d T ( k i ) + 1 ] × k i . p + ∑ i = 0 n [ d T ( d i ) + 1 ] × d i . p = 1 + ∑ i = 1 n d T ( k i ) × k i . p + ∑ i = 0 n d T ( d i ) × d i . p \begin{aligned} E[\text{Search cost in }T]&=\sum_{i=1}^n[d_T(k_i)+1]\times k_i.p+\sum_{i=0}^n[d_T(d_i)+1]\times d_i.p\\ &=1+\sum_{i=1}^nd_T(k_i)\times k_i.p+\sum_{i=0}^nd_T(d_i)\times d_i.p \end{aligned} E [ Search cost in T ] = i = 1 ∑ n [ d T ( k i ) + 1 ] × k i . p + i = 0 ∑ n [ d T ( d i ) + 1 ] × d i . p = 1 + i = 1 ∑ n d T ( k i ) × k i . p + i = 0 ∑ n d T ( d i ) × d i . p
求解最优二叉检索树就是找到这样一棵二叉搜索树T ∗ T^* T ∗ E ( T ∗ ) E(T^*) E ( T ∗ )
T ∗ = arg max T E ( T ) T^*=\arg\max_{T}E(T) T ∗ = arg T max E ( T )
问题分析 构造一棵任意的 BST 是简单的。我们只需对K K K k i k_i k i d i d_i d i
《算法导论》一书中指出,n n n Ω ( 4 n / n 3 / 2 ) \Omega(4^n/n^{3/2}) Ω ( 4 n / n 3/2 ) 指数爆炸问题 。因此下面将介绍一种使用动态规划 求解 OBST 的算法。
状态转移方程 现在我们从后往前 思考,对于一棵以k r k_r k r 包含 k r k_r k r k r k_r k r T 1 , T 2 T_1,\;T_2 T 1 , T 2
其中,T 1 T_1 T 1 k r k_r k r K 1 : = K < k 1 . . k r − 1 > K_1:=K<k_1..k_{r-1}> K 1 := K < k 1 .. k r − 1 > D 1 = D < d 0 . . d r − 1 > D_1=D<d_0..d_{r-1}> D 1 = D < d 0 .. d r − 1 > T 2 T_2 T 2 k r k_r k r K 2 : = K < k 1 . . k r − 1 > K_2:=K<k_1..k_{r-1}> K 2 := K < k 1 .. k r − 1 > D 2 D_2 D 2
k r K1: <k1,k2,...,kr-1> K2: <kr+1,kr+2,...,kn> T T1 T2 并且,以k r k_r k r T T T T 2 , T 2 T_2,\;T_2 T 2 , T 2 一个单位 。
E ( T ) = [ E ( T 1 ) + w ( 1 , k − 1 ) ] + [ E ( T 2 ) + w ( k + 1 , n ) ] + k r . p = E ( T 1 ) + E ( T 2 ) + [ w ( 1 , k − 1 ) + w ( k + 1 , n ) + k r . p ] = E ( T 1 ) + E ( T 2 ) + w ( 1 , n ) \begin{aligned} E(T)&=[E(T_1)+w(1,k-1)]+[E(T_2)+w(k+1,n)]+k_r.p\\ &=E(T_1)+E(T_2)+[w(1,k-1)+w(k+1,n)+k_r.p]\\ &=E(T_1)+E(T_2)+w(1,n) \end{aligned} E ( T ) = [ E ( T 1 ) + w ( 1 , k − 1 )] + [ E ( T 2 ) + w ( k + 1 , n )] + k r . p = E ( T 1 ) + E ( T 2 ) + [ w ( 1 , k − 1 ) + w ( k + 1 , n ) + k r . p ] = E ( T 1 ) + E ( T 2 ) + w ( 1 , n )
其中,w ( 1 , k − 1 ) w(1,k-1) w ( 1 , k − 1 ) E ( T 1 ) E(T_1) E ( T 1 ) 多出来的搜索代价 ,右子树同理。不难给出对于任意新增代价 w ( i , j ) w(i,j) w ( i , j )
w ( i , j ) = ∑ l = i j k l . p + ∑ l = i − 1 j d l . p w(i,j)=\sum_{l=i}^jk_l.p+\sum_{l=i-1}^jd_l.p w ( i , j ) = l = i ∑ j k l . p + l = i − 1 ∑ j d l . p
事实上,T 1 , T 2 T_1,\;T_2 T 1 , T 2 子问题 。我们只需要搜索 从K K K 以哪一个结点作为根结点 可以使得E ( T ) E(T) E ( T )
更一般化地,如果需要从子序列< k i , k i + 1 , . . . , k j > <k_i,k_{i+1},...,k_j> < k i , k i + 1 , ... , k j > 状态 ,在该状态下的最优值记作d p ( i , j ) dp(i,j) d p ( i , j )
d p ( i , j ) = { min i ≤ k ≤ j { d p ( i , k − 1 ) + d p ( k + 1 , j ) + w ( i , j ) } , j ≥ i d i − 1 . p , j = i − 1 dp(i,j)=\begin{cases} \min\limits_{i\leq k\leq j}\{dp(i,k-1)+dp(k+1,j)+w(i,j)\},&j\geq i\\ d_{i-1}.p,&j=i-1 \end{cases} d p ( i , j ) = ⎩ ⎨ ⎧ i ≤ k ≤ j min { d p ( i , k − 1 ) + d p ( k + 1 , j ) + w ( i , j )} , d i − 1 . p , j ≥ i j = i − 1
该状态方程指出,当划分出空子树 时,即j = i − 1 j=i-1 j = i − 1 j ≥ i j\geq i j ≥ i i → j i\to j i → j k k k
值得注意的是,我们的转移方程虽然建立起来了,但是我们还需关注自底向上 的数据是如何建立的。
例如,想要计算d p [ 1 , 5 ] dp[1,5] d p [ 1 , 5 ] d p [ 1 , 0 ] , d p [ 1 , 1 ] , d [ 1 , 2 ] , d p [ 1 , 3 ] , d p [ 1 , 4 ] dp[1,0],dp[1,1],d[1,2],dp[1,3],dp[1,4] d p [ 1 , 0 ] , d p [ 1 , 1 ] , d [ 1 , 2 ] , d p [ 1 , 3 ] , d p [ 1 , 4 ] d p [ 2 , 5 ] , d p [ 3 , 5 ] , d p [ 4 , 5 ] , d p [ 5 , 5 ] , d p [ 6 , 5 ] dp[2,5],dp[3,5],dp[4,5],dp[5,5],dp[6,5] d p [ 2 , 5 ] , d p [ 3 , 5 ] , d p [ 4 , 5 ] , d p [ 5 , 5 ] , d p [ 6 , 5 ]
而这些都需要我们一开始计算并保存过。下面给出将动态规划表旋转后的结果,该旋转使得数组的对角线元素在水平线上。
6 5 4 3 2 1 5 4 3 2 1 4 3 2 1 3 2 1 2 1 1 i j dp Table 0 5 1 6 图中的数字并不是实际结果,而是一个标记。可见只有在先算完图中标记为1 1 1 2 2 2 l l l 标记值-1,则:
l = 0 l=0 l = 0 i = 1 , 2 , 3 , 4 , 5 , 6. j = 0 , 1 , 2 , 3 , 4 , 5 i=1,2,3,4,5,6.\;j=0,1,2,3,4,5 i = 1 , 2 , 3 , 4 , 5 , 6. j = 0 , 1 , 2 , 3 , 4 , 5 j = i − 1 j=i-1 j = i − 1 l = 1 l=1 l = 1 i = 1 , 2 , 3 , 4 , 5. j = 1 , 2 , 3 , 4 , 5 i=1,2,3,4,5.\;j=1,2,3,4,5 i = 1 , 2 , 3 , 4 , 5. j = 1 , 2 , 3 , 4 , 5 l = 2 l=2 l = 2 i = 1 , 2 , 3 , 4. j = 2 , 3 , 4 , 5 i=1,2,3,4.\;j=2,3,4,5 i = 1 , 2 , 3 , 4. j = 2 , 3 , 4 , 5 l = 3 l=3 l = 3 i = 1 , 2 , 3. j = 3 , 4 , 5 i=1,2,3.\;j=3,4,5 i = 1 , 2 , 3. j = 3 , 4 , 5 l = 4 l=4 l = 4 i = 1 , 2. j = 4 , 5 i=1,2.\;j=4,5 i = 1 , 2. j = 4 , 5 l = 5 l=5 l = 5 i = 1. j = 5 i=1.\;j=5 i = 1. j = 5 d p [ 1 , 5 ] dp[1,5] d p [ 1 , 5 ] 根据以上自底向上的计算顺序,可总结出算法的循环体中应该有:i : 1 → n − l + 1 , j : i − l + 1 i:1\to n-l+1,\;j:i-l+1 i : 1 → n − l + 1 , j : i − l + 1
伪代码与复杂度 在算法中,为了简单起见,避免k i . p , d i . p k_i.p,\;d_i.p k i . p , d i . p K K K n n n p [ 1.. n ] p[1..n] p [ 1.. n ] q [ 1.. n + 1 ] q[1..n+1] q [ 1.. n + 1 ]
利用二维数组d p [ 1.. n + 1 , 0.. n ] dp[1..n+1,0..n] d p [ 1.. n + 1 , 0.. n ] j ≥ i − 1 j\geq i-1 j ≥ i − 1
d p [ . . ] dp[..] d p [ .. ] n + 1 n+1 n + 1 d p [ n + 1 , n ] dp[n+1,n] d p [ n + 1 , n ] k n k_n k n d n d_n d n d p [ 1 , 0 ] dp[1,0] d p [ 1 , 0 ] k 1 k_1 k 1 d 0 d_0 d 0
与d p [ . . ] dp[..] d p [ .. ] w [ 1.. n + 1 , 0.. n ] w[1..n+1,0..n] w [ 1.. n + 1 , 0.. n ]
w [ i , j ] = { w [ i , j − 1 ] + p [ j ] + q [ j ] , j ≥ i d i − 1 . p , j = i − 1 w[i,j]=\begin{cases} w[i,j-1]+p[j]+q[j],&j\geq i\\ d_{i-1}.p,&j=i-1 \end{cases} w [ i , j ] = { w [ i , j − 1 ] + p [ j ] + q [ j ] , d i − 1 . p , j ≥ i j = i − 1
为记录结果(追溯解 ),我们利用二维数组r o o t [ 1.. n , 1.. n ] root[1..n,1..n] roo t [ 1.. n , 1.. n ] r o o t [ i , j ] root[i,j] roo t [ i , j ] r r r 1 ≤ i ≤ j ≤ n 1\leq i\leq j\leq n 1 ≤ i ≤ j ≤ n
输入:关键字序列K K K n n n p [ 1.. n ] p[1..n] p [ 1.. n ] q [ 1.. n + 1 ] q[1..n+1] q [ 1.. n + 1 ] 输出:OBST的最小代价,根结点的选取表r o o t [ 1.. n , 1.. n ] root[1..n,1..n] roo t [ 1.. n , 1.. n ] Algorithm: Optimal-BST ( n , p , q ) 1. 初始化二维数组 d p , w , r o o t 2. f o r i = 1 t o n + 1 d o 3. d p [ i , i − 1 ] ← q [ i − 1 ] 4. w [ i , i − 1 ] ← q [ i − 1 ] 5. f o r l = 1 t o n d o 6. f o r i = 1 t o n − l + 1 d o 7. j ← i + l − 1 8. d p [ i , j ] ← + ∞ 9. w [ i , j ] ← w [ i , j − 1 ] + p [ j ] + q [ j ] 10. f o r r = i t o j d o 11. t m p ← d p [ i , r − 1 ] + d p [ r + 1 , j ] + w [ i , j ] 12. i f d p [ i , j ] > t m p t h e n 13. d p [ i , j ] ← t m p 14. r o o t [ i , j ] ← r 15. r e t u r n d p [ 1 , n ] a n d r o o t \begin{aligned} &\text{Algorithm: }\;\text{Optimal-BST}(n,p,q)\\\\ 1.&\;\text{初始化二维数组 }dp,\;w,\;root\\ 2.&\;\mathbf{for}\;i\;=1\;\mathbf{to}\;n+1\;\mathbf{do}\\ 3.&\;\qquad dp[i,i-1]\leftarrow q[i-1]\\ 4.&\;\qquad w[i,i-1]\leftarrow q[i-1]\\ 5.&\;\mathbf{for}\;l\;=1\;\mathbf{to}\;n\;\mathbf{do}\\ 6.&\;\qquad\mathbf{for}\;i\;=1\;\mathbf{to}\;n-l+1\;\mathbf{do}\\ 7.&\;\qquad\qquad j\leftarrow i+l-1\\ 8.&\;\qquad\qquad dp[i,j]\leftarrow +\infty\\ 9.&\;\qquad\qquad w[i,j]\leftarrow w[i,j-1]+p[j]+q[j]\\ 10.&\;\qquad\qquad\mathbf{for}\;r\;=i\;\mathbf{to}\;j\;\mathbf{do}\\ 11.&\;\qquad\qquad\qquad tmp\leftarrow dp[i,r-1]+dp[r+1,j]+w[i,j]\\ 12.&\;\qquad\qquad\qquad\mathbf{if}\;dp[i,j]\gt tmp\;\mathbf{then}\\ 13.&\;\qquad\qquad\qquad\qquad dp[i,j]\leftarrow tmp\\ 14.&\;\qquad\qquad\qquad\qquad root[i,j]\leftarrow r\\ 15.&\;\mathbf{return}\;dp[1,n]\;\mathbf{and}\;root \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Algorithm: Optimal-BST ( n , p , q ) 初始化二维数组 d p , w , roo t for i = 1 to n + 1 do d p [ i , i − 1 ] ← q [ i − 1 ] w [ i , i − 1 ] ← q [ i − 1 ] for l = 1 to n do for i = 1 to n − l + 1 do j ← i + l − 1 d p [ i , j ] ← + ∞ w [ i , j ] ← w [ i , j − 1 ] + p [ j ] + q [ j ] for r = i to j do t m p ← d p [ i , r − 1 ] + d p [ r + 1 , j ] + w [ i , j ] if d p [ i , j ] > t m p then d p [ i , j ] ← t m p roo t [ i , j ] ← r return d p [ 1 , n ] and roo t
显然,算法嵌套了三层循环,每层执行的操作在O ( 1 ) O(1) O ( 1 ) Θ ( n 3 ) \Theta(n^3) Θ ( n 3 ) n × n n\times n n × n O ( n 2 ) O(n^2) O ( n 2 )
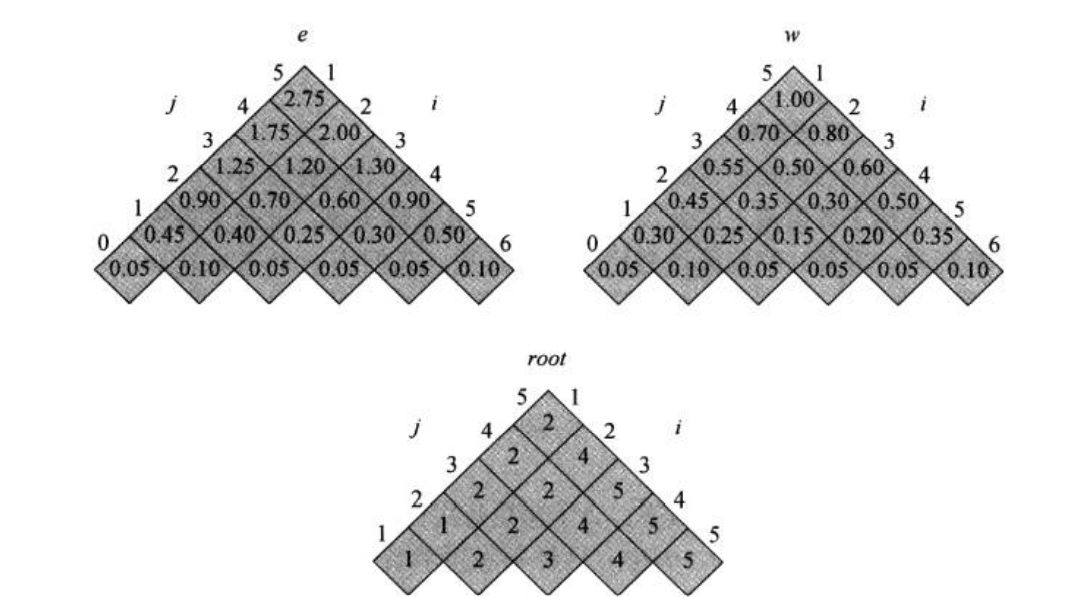
实例与编程 假设给定概率分布 如下:
i i i 0 1 2 3 4 5 p [ i ] p[i] p [ i ] 0.15 0.10 0.05 0.10 0.20 q [ i ] q[i] q [ i ] 0.05 0.10 0.05 0.05 0.05 0.10
下给出 c 系列的编程实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 #include <iostream> #include <algorithm> #include <string.h> #include <vector> #include <queue> #include <cstdlib> using namespace std;#define M 100 double dp[M][M];double w[M][M];int root[M][M];double Optimal_BST (double p[], double q[], int n) memset (dp,0 ,sizeof (dp)); memset (root,0 ,sizeof (root)); memset (w,0 ,sizeof (w)); for (int i = 1 ; i <= n+1 ; i++){ dp[i][i-1 ] = q[i-1 ]; w[i][i-1 ] = q[i-1 ]; } for (int l = 1 ; l <= n; l++){ for (int i = 1 ; i <= n-l+1 ; i++){ int j = i+l-1 ; dp[i][j] = INT32_MAX; w[i][j] = w[i][j-1 ]+p[j]+q[j]; for (int r = i; r <= j; r++){ double tmp = dp[i][r-1 ]+dp[r+1 ][j]+w[i][j]; if (dp[i][j] > tmp){ dp[i][j] = tmp; root[i][j] = r; } } } } return dp[1 ][n]; } int main (void ) double p[6 ] = {0 , 0.15 , 0.10 , 0.05 , 0.10 , 0.20 }; double q[6 ] = {0.05 , 0.10 , 0.05 , 0.05 , 0.05 , 0.10 }; cout << "min E = " << Optimal_BST (p, q, 5 ) << endl << endl; for (int l = 0 ; l <= 5 ; l++){ for (int i = 1 ; i <= 5 -l+1 ; i++){ int j = i+l-1 ; cout << "(" << i << "," << j << "): dp = " ; printf ("%.2f\t" ,dp[i][j]); cout << "w = " ; printf ("%.2f\t" ,w[i][j]); cout << "root = " << root[i][j] << endl; } } return 0 ; }
得到如下旋转过后的各数组结果:
从而得到对于该问题的最小代价为2.75 2.75 2.75
最小生成树|Minimum Spanning Tree,MST 对于一个 无向带权连通图 G = ( V , E , W ) G=(V,E,W) G = ( V , E , W ) G G G 无环子集 T T T T ⊆ G T\subseteq G T ⊆ G T T T G G G w ( T ) = ∑ ( u , v ) ∈ T w ( u , v ) w(T)=\sum\limits_{(u,v)\in T}w(u,v) w ( T ) = ( u , v ) ∈ T ∑ w ( u , v )
由T T T T T T T T T G G G 最小生成树 Minimum Spanning Tree,MST。
生成树的性质 生成树具有如下性质 G ( V , E , W ) G(V,E,W) G ( V , E , W ) n n n ∣ V ∣ = n |V|=n ∣ V ∣ = n
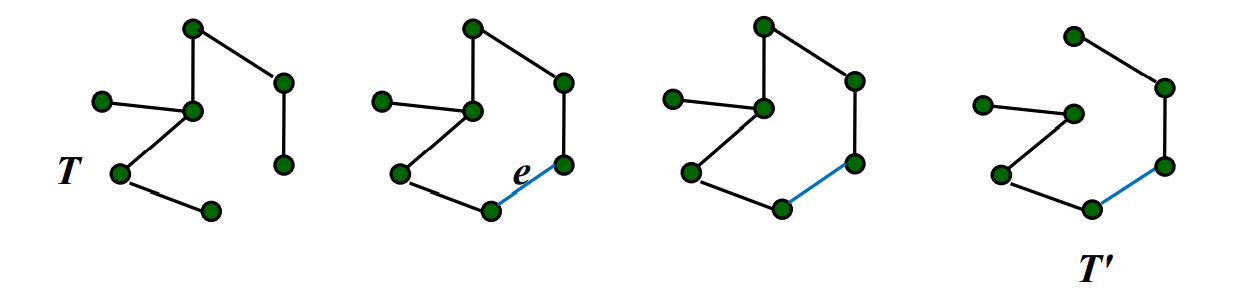
T T T G G G T T T n − 1 n-1 n − 1 若某条边e ∈ E ( G ) e\in E(G) e ∈ E ( G ) G G G T T T e e e e ∉ E ( T ) e\notin E(T) e ∈ / E ( T ) E ( T ) ∪ { e } E(T)\cup \{e\} E ( T ) ∪ { e } C C C E ( X ) E(X) E ( X ) X X X 边集 ) 紧接第二点,如果去掉回路C C C e ′ , e ′ ≠ e e',\quad e'\neq e e ′ , e ′ = e T ′ T' T ′ 如下图所示:
根据该性质,我们可以初步得出一种找到 MST 的策略:T T T e e e C C C C C C e ′ e' e ′ w ( e ′ ) < w ( e ) w(e')\lt w(e) w ( e ′ ) < w ( e ) T ′ T' T ′ w ( T ′ ) − w ( T ) = w ( e ′ ) − w ( e ) < 0 w(T')-w(T)=w(e')-w(e)\lt0 w ( T ′ ) − w ( T ) = w ( e ′ ) − w ( e ) < 0 w ( T ′ ) < w ( T ) w(T')\lt w(T) w ( T ′ ) < w ( T )
从而可以根据该策略不断改进,最终得到 MST.
于是,求出一棵生成树的问题也就可以按照如下的通用算法进行描述:
Algorithm: Generic-MST ( G , E , w ) 1. A ← ∅ 2. w h i l e A does not from a spanning tree d o 3. find an edge ( u , v ) that is safe for A 4. A ← A ∪ { ( u , v ) } 5. r e t u r n A \begin{aligned} &\text{Algorithm: }\;\text{Generic-MST}(G,E,w)\\\\ 1.&\;A\leftarrow\varnothing\\ 2.&\;\mathbf{while}\;A\text{ does not from a spanning tree}\;\mathbf{do}\\ 3.&\;\qquad \text{find an edge }(u,v)\text{ that is safe for }A\\ 4.&\;\qquad A\leftarrow A\cup\{(u,v)\}\\ 5.&\;\mathbf{return}\;A \end{aligned} 1. 2. 3. 4. 5. Algorithm: Generic-MST ( G , E , w ) A ← ∅ while A does not from a spanning tree do find an edge ( u , v ) that is safe for A A ← A ∪ {( u , v )} return A
此处的A A A s a f e safe s a f e ( u , v ) (u,v) ( u , v ) A ∪ { ( u , v ) } A\cup\{(u,v)\} A ∪ {( u , v )} 安全边 .
下面将具体介绍两种算法用于求解最小生成树,并且二者均是利用了贪心策略 的思想,但具体如何找到安全边的方法则不一样。
Prim算法 Prim 算法的核心思想是将图的顶点V V V S , V − S S,V-S S , V − S e = ( u , v ) e=(u,v) e = ( u , v ) u ∈ S , v ∈ V − S u\in S,v\in V-S u ∈ S , v ∈ V − S e e e 横跨 V V V 切割 ( S , V − S ) (S,V-S) ( S , V − S )
而 Prim算法 要求不断找到横跨某个切割的最小权重边,这样的边称为 轻量级边 。可以证明这样的轻量级边就是一条安全边 。
Prim算法 将当前的轻量级边划入子集A A A S S S S S S
说人话就是,初始化最终 MST 的点集和边集为空。距离最近的边 ,然后将此边的连接的另一个端点加入点集,此边加入边集。当前这个点集 最近的边,依次加入,直到所有顶点都加入点集。
算法伪码 输入:连通图G G G w w w r r r 输出:最小生成树的边集A A A 其他:v . k e y v.key v . k ey v v v 权重 ,若不存在则赋为∞ \infty ∞ v . π v.\pi v . π v v v 边 e = ( v , v . π ) e=(v,v.\pi) e = ( v , v . π ) v . k e y v.key v . k ey G . V G.V G . V G G G V ( G ) V(G) V ( G ) G . A d j [ v ] G.Adj[v] G . A d j [ v ] G G G v v v N G ( v ) N_G(v) N G ( v ) Algorithm: MST-Prim ( G , w , r ) / / r 是起始点,最终作为树的根结点 1. f o r each u ∈ G . V d o 2. u . k e y ← + ∞ 3. u . π ← N I L 4. r . k e y ← 0 5. Q ← G . V / / Q 为按权重 V . k e y 递增的优先队列 6. A ← ∅ 7. w h i l e Q ≠ ∅ d o 8. u ← Extract-min ( Q ) 9. A ← A ∪ { ( u , u . π ) } 10. f o r each v ∈ G . A d j [ u ] d o 11. i f v ∈ Q and w ( u , v ) < v . k e y t h e n 12. v . π ← u 13. v . k e y ← w ( u , v ) 14. r e t u r n A \begin{aligned} &\text{Algorithm: }\;\text{MST-Prim}(G,w,r)\\ &//r\text{是起始点,最终作为树的根结点}\\\\ 1.&\;\mathbf{for}\;\text{each }u\in G.V\;\mathbf{do}\\ 2.&\;\qquad\;u.key\leftarrow+\infty\\ 3.&\;\qquad\;u.\pi\leftarrow NIL\\ 4.&\;r.key\leftarrow0\\ 5.&\;Q\leftarrow G.V\;//Q\text{为按权重 }V.key\text{ 递增的优先队列}\\ 6.&\;A\leftarrow\varnothing\\ 7.&\;\mathbf{while}\;Q\neq\varnothing\;\mathbf{do}\\ 8.&\;\qquad u\leftarrow\text{Extract-min}(Q)\\ 9.&\;\qquad A\leftarrow A\cup\{(u,u.\pi)\}\\ 10.&\;\qquad\mathbf{for}\;\text{each }v\in G.Adj[u]\;\mathbf{do}\\ 11.&\;\qquad\qquad\mathbf{if}\;v\in Q\text{ and }w(u,v)\lt v.key\;\mathbf{then}\\ 12.&\;\qquad\qquad\qquad v.\pi\leftarrow u\\ 13.&\;\qquad\qquad\qquad v.key\leftarrow w(u,v)\\ 14.&\;\mathbf{return}\;A \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. Algorithm: MST-Prim ( G , w , r ) // r 是起始点,最终作为树的根结点 for each u ∈ G . V do u . k ey ← + ∞ u . π ← N I L r . k ey ← 0 Q ← G . V // Q 为按权重 V . k ey 递增的优先队列 A ← ∅ while Q = ∅ do u ← Extract-min ( Q ) A ← A ∪ {( u , u . π )} for each v ∈ G . A d j [ u ] do if v ∈ Q and w ( u , v ) < v . k ey then v . π ← u v . k ey ← w ( u , v ) return A
其中,第10到13行是对队列中的结点的属性进行更新 ,使得每次循环都能保证队列中的结点v v v A A A v . k e y v.key v . k ey A A A v v v v . π v.\pi v . π
如果优先队列Q Q Q 最小二叉堆 实现,则每一次循环取出当前最小元的过程(利用最小二叉堆实现时)需要花费O ( log ∣ V ∣ ) O(\log |V|) O ( log ∣ V ∣ ) while 循环次数O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ ) for 循环总次数O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
综合来看,该算法的时间复杂度为O ( ∣ V ∣ log ∣ V ∣ + ∣ E ∣ log ∣ V ∣ ) = O ( ∣ E ∣ log ∣ V ∣ ) O(|V|\log |V|+|E|\log |V|)=O(|E|\log |V|) O ( ∣ V ∣ log ∣ V ∣ + ∣ E ∣ log ∣ V ∣ ) = O ( ∣ E ∣ log ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
如果改用斐波那契堆,则时间复杂度还可以进一步优化为O ( ∣ E ∣ + ∣ V ∣ log ∣ V ∣ ) O(|E|+|V|\log|V|) O ( ∣ E ∣ + ∣ V ∣ log ∣ V ∣ )
正确性证明 提出命题 ∀ k < n = ∣ V ∣ \forall k\lt n=|V| ∀ k < n = ∣ V ∣ k k k A A A
当k = 1 k=1 k = 1 T ∗ T^* T ∗ r r r ( r , i ) (r,i) ( r , i ) ( r , i ) ∉ T ∗ (r,i)\notin T^* ( r , i ) ∈ / T ∗ T = ( T ∗ − { ( r , j ) } ) ∪ { ( r , i ) } T=(T^*-\{(r,j)\})\cup\{(r,i)\} T = ( T ∗ − {( r , j )}) ∪ {( r , i )} ( r , i ) (r,i) ( r , i ) w ( r , i ) = min ( r , t ) ∈ E w ( r , t ) ≤ w ( r , j ) w(r,i)=\min\limits_{(r,t)\in E}w(r,t)\leq w(r,j) w ( r , i ) = ( r , t ) ∈ E min w ( r , t ) ≤ w ( r , j ) 替换后得到的生成树仍然是最优解
现 假设命题成立 ,证明命题对k + 1 k+1 k + 1
设算法当前得到的子集A A A S S S k + 1 k+1 k + 1 V − S V-S V − S i k + 1 i_{k+1} i k + 1 S S S i k + 1 i_{k+1} i k + 1 S S S
假设该最小权边记为e = ( i k + 1 , i l ) e=(i_{k+1},i_l) e = ( i k + 1 , i l ) e ∈ T e\in T e ∈ T e e e T ∗ T^* T ∗ ( S , V − S ) (S,V-S) ( S , V − S ) e ′ e' e ′
T = ( T ∗ − { e ′ } ) ∪ { e } T=(T^*-\{e'\})\cup\{e\} T = ( T ∗ − { e ′ }) ∪ { e }
因为e e e w ( e ) ≤ w ( e ′ ) , w ( T ) ≤ w ( T ∗ ) w(e)\leq w(e'),w(T)\leq w(T^*) w ( e ) ≤ w ( e ′ ) , w ( T ) ≤ w ( T ∗ ) T T T k + 1 k+1 k + 1
当算法执行完毕后,结果A = T A=T A = T G G G
编程实现 采用 C++ 进行编程实现.
首先创建给出结果的边集结构体(Edge),以及由 Node 和 Edge 数组组合而成的图(Graph).
此外还有为Prim算法设计的优先队列,因为C++中没有特定的Decrease-key() 方法,因此直接采用 vector +遍历的方法模拟优先队列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 typedef struct NODE { int tag; int key; int pi; }Node; typedef struct EDGE { int u,v; }Edge; typedef struct GRAPH { int num; vector<int > nodes; vector<Edge> edges; }Graph;
然后是具体的Prim算法实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 Node PopMinKey (vector<Node> &Q) { int min = INT32_MAX; Node u; int index; for (int i = 0 ; i < Q.size (); i++){ if (min > Q[i].key){ min = Q[i].key; u = Q[i]; index = i; } } Q.erase (Q.begin ()+index); return u; } void UpdateQueue (vector<Node> &Q, int target, int sourse, int weight) for (int i = 0 ; i < Q.size (); i++){ if (Q[i].tag == target){ Q[i].key = weight; Q[i].pi = sourse; break ; } } } vector<Edge> MST_Prim (Graph G, int w[], int r = 0 ) { vector<Node> Q; for (int i = 0 ; i < G.num; i++){ Q.push_back ({G.nodes[i], INT32_MAX, -1 }); } Q[0 ].key = 0 ; Q[0 ].pi = 1 ; vector<Edge> A; while (!Q.empty ()){ Node u = PopMinKey (Q); A.push_back ({u.tag, u.pi}); for (int i = 0 ; i < G.edges.size (); i++){ if (G.edges[i].u == u.tag){ UpdateQueue (Q, G.edges[i].v, u.tag, w[i]); } if (G.edges[i].v == u.tag){ UpdateQueue (Q, G.edges[i].u, u.tag, w[i]); } } } return A; }
实例演示
3 1 2 4 5 6 6 3 6 5 6 4 2 1 5 5 3 1 2 4 5 6 6 3 6 5 6 4 2 1 5 5 3 1 2 4 5 6 6 3 6 5 6 4 2 1 5 5 3 1 2 4 5 6 6 3 6 5 6 4 2 1 3 1 2 4 5 6 3 6 5 6 4 2 1 3 1 2 4 5 6 3 5 4 2 1 编写主函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int main (void ) Graph G; int u,v; G.num = 6 ; for (int i = 0 ; i < 6 ; i++){ G.nodes.push_back (i+1 ); } for (int i = 0 ; i < 10 ; i++){ cin >> u >> v; G.edges.push_back ({u,v}); } int w[10 ]= {6 ,1 ,5 ,5 ,3 ,5 ,6 ,4 ,2 ,6 }; vector<Edge> MST = MST_Prim (G,w); for (int i = 1 ; i < MST.size (); i++){ cout << "(" << MST[i].u << ", " << MST[i].v << ")" << endl; } while (1 ); }
结果如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 输入(边集): 1 2 1 3 1 4 2 3 2 5 3 4 3 5 3 6 4 6 5 6 输出(边集): (3, 1) (6, 3) (4, 6) (2, 3) (5, 2)
Prefect!
Kruskal算法 Kruskal 算法的核心是与 Prim算法 不同。最小权边 都是相互连通的。换言之,Kruskal算法中第k k k A A A
不难发现,Prim算法因为每一步仅选取一个点及其轻量级边纳入A A A A A A 判断是否构成回路的策略 。这个策略可以利用并查集 这种数据结构解决。
综上,Kruskal算法的思想就是,先对边集进行升序排列 ,然后考察当前最小边纳入A A A
算法伪码 输入:连通图G G G w w w 输出:最小生成树的边集A A A Algorithm: MST-Kruskal ( G , w ) 1. f o r each u ∈ G . V d o 2. Make-Set ( u ) 3. Q ← G . E / / Q 为按权重 w ( e ) 递增的优先队列 4. A ← ∅ 5. r e p e a t 6. ( u , v ) ← Extract-min ( Q ) 7. i f Find-Set ( u ) ≠ Find-Set ( u ) t h e n 8. A ← A ∪ { ( u , u . π ) } 9. Union ( u , v ) 10. u n t i l ∣ A ∣ = ∣ V ∣ − 1 11. r e t u r n A \begin{aligned} &\text{Algorithm: }\;\text{MST-Kruskal}(G,w)\\\\ 1.&\;\mathbf{for}\;\text{each }u\in G.V\;\mathbf{do}\\ 2.&\;\qquad\;\text{Make-Set}(u)\\ 3.&\;Q\leftarrow G.E\;//Q\text{为按权重 }w(e)\text{ 递增的优先队列}\\ 4.&\;A\leftarrow\varnothing\\ 5.&\;\mathbf{repeat}\\ 6.&\;\qquad (u,v)\leftarrow\text{Extract-min}(Q)\\ 7.&\;\qquad\mathbf{if}\;\text{Find-Set}(u)\neq\text{Find-Set}(u)\;\mathbf{then}\\ 8.&\;\qquad\qquad A\leftarrow A\cup\{(u,u.\pi)\}\\ 9.&\;\qquad\qquad\text{Union}(u,v)\\ 10.&\;\mathbf{until}\;|A|=|V|-1\\ 11.&\;\mathbf{return}\;A \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. Algorithm: MST-Kruskal ( G , w ) for each u ∈ G . V do Make-Set ( u ) Q ← G . E // Q 为按权重 w ( e ) 递增的优先队列 A ← ∅ repeat ( u , v ) ← Extract-min ( Q ) if Find-Set ( u ) = Find-Set ( u ) then A ← A ∪ {( u , u . π )} Union ( u , v ) until ∣ A ∣ = ∣ V ∣ − 1 return A
其中:
Make-Set ( u ) \text{Make-Set}(u) Make-Set ( u ) Find-Set ( u ) \text{Find-Set}(u) Find-Set ( u ) u u u ( u , v ) (u,v) ( u , v ) Union ( u , v ) \text{Union}(u,v) Union ( u , v ) u , v u,v u , v 分析得知,一共循环O ( ∣ E ∣ ) O(|E|) O ( ∣ E ∣ ) O ( log ∣ E ∣ ) O(\log |E|) O ( log ∣ E ∣ ) O ( ∣ E ∣ log ∣ E ∣ ) O(|E|\log |E|) O ( ∣ E ∣ log ∣ E ∣ ) ∣ E ∣ ≤ ∣ V ∣ 2 |E|\leq|V|^2 ∣ E ∣ ≤ ∣ V ∣ 2 O ( ∣ E ∣ log ∣ V ∣ ) O(|E|\log|V|) O ( ∣ E ∣ log ∣ V ∣ ) O ( ∣ V ∣ ) O(|V|) O ( ∣ V ∣ )
正确性证明 利用数学归纳法 .∣ V ∣ = n |V|=n ∣ V ∣ = n G G G
n = 2 n=2 n = 2 G G G 最小权边 ,显然能够得到最小生成树;假设 对于任意n n n n + 1 n+1 n + 1 对于任意n + 1 n+1 n + 1 G G G e = ( i , j ) e=(i,j) e = ( i , j ) 短接 ,如下图所示,将图化为n n n G ′ G' G ′ G ′ G' G ′ T ′ T' T ′
1 3 2 4 5 6 短接 1 3 2 5 4-6 G G' 1 3 2 5 4-6 T' 1 3 2 4 5 6 恢复 T MST 则T = T ′ ∪ { e } T=T'\cup\{e\} T = T ′ ∪ { e } G G G ∃ T ∗ ∋ e \exists T^*\ni e ∃ T ∗ ∋ e G G G
注:就算e ∉ T ∗ e\notin T^* e ∈ / T ∗ e e e
此时,有w ( T ∗ ) < w ( T ) ⇒ w ( T ∗ − { e } ) < w ( T − { e } ) = w ( T ′ ) w(T*)\lt w(T)\Rightarrow w(T^*-\{e\})\lt w(T-\{e\})=w(T') w ( T ∗ ) < w ( T ) ⇒ w ( T ∗ − { e }) < w ( T − { e }) = w ( T ′ ) T ′ T' T ′ G ′ G' G ′
综上所述,Kruskal 算法能够给出任意n n n
编程实现 采用 C++ 进行编程实现.
首先声明必要的结构体以及以边权大小排序的优先队列:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 typedef struct EDGE { int u,v; int w; }Edge; typedef struct GRAPH { int num; vector<int > nodes vector<Edge> edges; }Graph; struct cmp { bool operator () (Edge a, Edge b) return a.w > b.w; } }; typedef priority_queue<Edge,vector<Edge>,cmp> EdgeQue;
利用 vector 自建并查集及其相关的合并查找函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 typedef struct SET { int root; int value; }Set; vector<Set> MakeSet (vector<int > a) { vector<Set> set (a.size()) ; for (int i = 0 ; i < a.size (); i++){ set[i].root = a[i]; set[i].value = a[i]; } return set; } void SetUnion (vector<Set> &set, int a, int b) int i = max (set[a].root, set[b].root); int j = min (set[a].root, set[b].root); for (int k = 0 ; k < set.size (); k++){ if (set[k].root == i){ set[k].root = j; } } }
最后是 Kruskal算法的实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 vector<Edge> MST_Kruskal (Graph G) { vector<Edge> A; vector<Set> set = MakeSet (G.nodes); EdgeQue Q; for (int i = 0 ; i < G.edges.size (); i++){ Q.push ({G.edges[i].u, G.edges[i].v, G.edges[i].w}); } do { Edge e = Q.top (); Q.pop (); if (set[e.u].root != set[e.v].root){ A.push_back ({e.u, e.v}); SetUnion (set, e.u, e.v); } } while (A.size () < G.num-1 ); return A; }
利用和 Prim进行演示时相同的实例,编写主函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int main (void ) Graph G; int u,v; G.num = 6 ; int w[10 ]= {6 ,1 ,5 ,5 ,3 ,5 ,6 ,4 ,2 ,6 }; for (int i = 0 ; i < 6 ; i++){ G.nodes.push_back (i+1 ); } for (int i = 0 ; i < 10 ; i++){ cin >> u >> v; G.edges.push_back ({u,v,w[i]}); } vector<Edge> MST = MST_Kruskal (G); for (int i = 0 ; i < MST.size (); i++){ cout << "(" << MST[i].u << ", " << MST[i].v << ")" << endl; } while (1 ); }
结果如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 输入(边集): 1 2 1 3 1 4 2 3 2 5 3 4 3 5 3 6 4 6 5 6 输出(边集): (1, 3) (4, 6) (2, 5) (3, 6) (2, 3)
Prefect!
参考 《算法导论 (原书第三版)》 算法设计与分析|中国大学MOOC 哈夫曼树(赫夫曼树、最优树)详解 C++优先队列自定义排序总结|CSDN