时空/动态图神经网络：因子与耦合艺术

前言

在利用深度学习方法处理图结构数据方面，本站文章（图网络浅学：图神经网络及其发展 - GNN）已经做了不少介绍。这些经典的图神经网络方法很好地适应了静态图（Static Graph）的情况——图的结构和特征固定不变，仅在空间上进行模式识别。

然而在很多其他研究中，例如交通流量预测、人类活动轨迹预测等任务，通常需要同时考虑空间依赖性和时间依赖性。也就是说，这类任务建模出来的图结构可能是会随着时间的变化而变化的。这种变化可能是节点或边随着时间的增加与减少，也可能是节点特征和边特征随时间的改变。与静态图对应，这类图结构我们称为动态图（Dynamic Graph），事实上还有诸如时空图（Spatio-temporal Graph）、时空依赖图等术语。这些术语的定义来源于不同的论文、不同的研究者及其相关的不同领域。所以为了统一概念，此后本文都称为动态图，并会继续给出严谨的定义和分类。

那么“动态图的深度学习模型应该如何构建？”、“目前有哪些研究？”就是本篇文章的核心了。
本文的分类结构和部分内容继承自文献《Dynamic Graph Representation Learning with Neural Networks: A Survey》、 《Spatio-Temporal Graph Neural Networks for Predictive Learning in Urban Computing: A Survey》，在此基础上加入了一些个人理解和其他未提及的模型。

图神经网络开发库Pytorch-Geometric 也有对应的时空图扩展：

🧬PyG-Temporal扩展： https://github.com/benedekrozemberczki/pytorch_geometric_temporal

动态化程度

Dynamic Graph: A dynamic graph is a graph whose topology and/or attributes change over time.

从动态图的定义中我们可以看出，边和节点的消失与增加、边特征和节点特征随时间的变化，这几种可能任意组合都是一种动态图。为此我们需要引入动态化程度（degree of dynamism）的概念：

理论上一个动态图，有四种可能的情况：

1. 图的点集$V$ 和边集$E$ 都不变，记为$fix_{V,E}$。这种情况被很多文献称为"时空图"或"时空图" ( Spatial-Temporal Graphs，Spatio-Temporal Graphs，STGs)；
2. $V$ 不变但$E$ 变，指会动态地增加或删除，记为$fix_V$；
3. $V,E$ 都变，记为$vary$；
4. $E$ 不变但$V$ 变。由于一条边是基于一组节点而存在的，所以这种情况没意义。

动态图类型

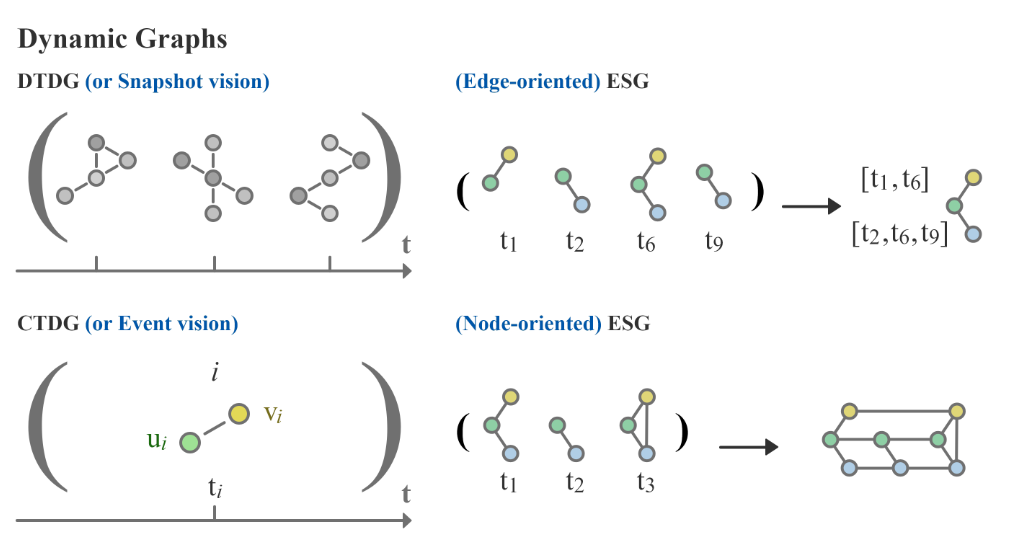
连续时间动态图

为了保留准确的时间信息，连续时间动态图 (Continuous Time Dynamic Graphs，CTDGs) 使用一组事件（Event）来表示动态图。

如文献 《Foundations and Modeling of Dynamic Networks Using Dynamic Graph Neural Networks: A Survey》 主要关注边的动态性，概述了三种典型的表示学习方法，它通过给定的一对节点$(u_i , v_i)$ 和时间$t_i$ 对事件进行表示：

1. $Contact\text{-}Sequence=\{(u_i,v_i,t_i)\}$ 表示$t$ 时刻两个节点$(u , v)$ 之间的瞬时交互；
2. $Event\text{-}Based=\{(u_i,v_i,t_i,\Delta_i)\}$ 表示$t$ 时刻两个节点$(u , v)$ 之间持续$\Delta$ 时间的交互；
3. $Graph\text{-}Stream=\{(u_i,v_i,t_i,\delta_i)\}$ 常用于大规模的图结构中，表示$t$ 时刻两个节点$(u , v)$ 之间的交互：$\delta=1$ 是增加、$\delta=-1$ 是删除；

离散时间动态图

离散时间动态图 (Discrete-time dynamic graphs，DTDGs) 可以看作由$T$ 个静态图组成的序列，它们是动态图在不同时刻或时间窗口的快照 (snapshots)。

$$DTDG=(G^1,G^2,..,G^T)$$

等效静态图

等效静态图 (Equivalent Static Graphs，ESGs) 的表示方法是构建一个单一的静态图用来表示一个动态图。近年来提出了几种构建ESG的方法，我们将其分为面向边（Edge-oriented）的和面向节点 （Node-oriented）的。

• Edge-oriented ESG 将图序列聚合成具有时间信息的静态图，编码为序列属性，也被称为 time-then-graph 的表示方法；
• Node-oriented ESG 在顶点出现的每个时刻构建顶点的副本，并定义节点在时间戳/事件之间的连接方式。进一步的细节将后文中继续讨论。

下图展示了以上三种类型的动态图示意：

模型架构

一种基本的时空图神经网络模型架构如下图所示。

• 数据处理模块（Data Processing Module，DPM）：从原始数据中构建时空图数据；
• 时空图学习模块（Spatio-Temporal Graph Learning Module，STGLM）：捕获复杂的社会系统中隐藏的时空依赖关系；
• 任务感知预测模块（Task-aware Prediction Module，TPM）：将STGLM中的时空隐藏表示映射到下游预测任务的空间中。

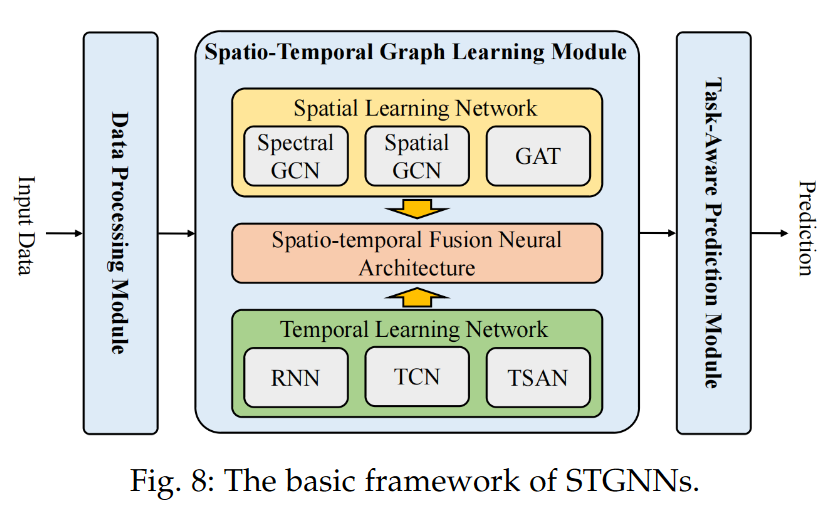
显然，STGLM 是 STGNN 中最关键的部分。可以看到这是一种十分自然的构思：将用于空间结构的网络和用于时间序列的网络进行融合。

其中，空间结构上的网络都是我们介绍过的谱域图卷积网络、空域图卷积网络、图注意力网络GAT等方法；而用于处理时间序列的网络也是我们学习过的网络：循环神经网络|RNN、时间卷积网络TCN、时间自注意力网络TSAN。

因此，STGLM 中最主要的就是如何将这两种网络融合起来，即时空融合架构（Spatio-temporal Fusion Neural Architecture）如何设计。

传统的融合神经架构可以分为两类：因子神经架构（Factorized Neural Architecture）和耦合神经架构（Coupled Neural Architecture）。

因子神经架构

在因子神经架构中，空间学习网络和时间学习网络模块一层一层并行或串行堆叠。两种典型的因子神经架构的模型分别是 STGCN 和 T-GCN。

STGCN

📑Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting

🧬官方TensorFlow实现： https://github.com/VeritasYin/STGCN_IJCAI-18

STGCN 输入 $M$ 个时间步的图的特征向量 $\mathbf X\in\Bbb R^{M\times n\times C_i}$ （$C_i$ 表示输入通道/输入特征数，$n$ 表示节点数）以及对应的邻接矩阵 $W\in\Bbb R^{n\times n}$，经过两个$\text{ST-Conv\;Block}$ 和一个输出层，输出 $\hat{v}\in\Bbb R^{n\times C_o}$ （$C_o$ 表示输出通道/输出特征数）来预测第 $t+1$ 个时间步的节点特征。

具体来说，STGCN在时域上使用门控时间卷积网络，在空间上使用 ChebGCN，二者按三明治结构串联堆叠，形成一个$\text{ST-Conv\;Block}$，如下图所示。

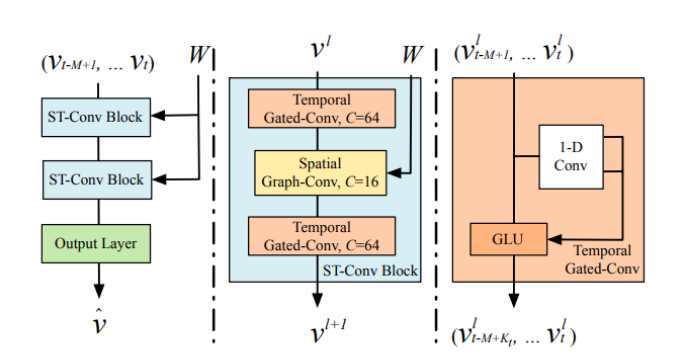
由于该模型通过卷积结构学习时间信息，所以其时空学习方法是并行的，即同时接收给定时间窗口长度$K_t$ 的所有信息作为输入。

作者受到GRU的启发，在$\text{1D-Conv}$ 内再附加门控线性单元（Gated Linear Unit，GLU）以提高时间学习的能力。

具体来说，先是根据时间卷积的原理，设卷积核为$\Gamma\in\Bbb R^{K_t\times C_i\times2 C_o}$ ，它实际上是由两组卷积核组成，每组内有$C_o$ 个卷积核（为了输出$C_o$ 个通道），两组卷积核分别对每一个节点特征$X^{(i)}\in\Bbb R^{M\times C_i}$ 进行卷积得到两个结果$P^{(i)},Q^{(i)}\in\Bbb R^{(M-K_t+1)\times C_o}$ ，而$\text{GLU}$ 在论文中就是对$P,Q$ 进行如下运算：

$$\Gamma*_{\tau}X^{(i)}=P^{(i)}\odot\sigma(Q^{(i)})$$

下面我们记$\Gamma*_{\tau}$ 就是对输入进行上述卷积运算，记$\Theta*_{\cal G}$ 为对输入进行 ChebGCN 运算（值得注意的是，该模型还对每次的图卷积增加了残差连接）。

最终，这个模型中每个$\text{ST-Conv\;Block}$ 的计算可以定义如下：

$$v^{(l+1)}=\Gamma^{l}_1*_{\tau}\text{ReLU}\left(\Theta^{l}*_{\cal G}(\Gamma^{l}_0*_{\tau}v^{(l)})\right)$$

经过有限个$\text{ST-Conv\;Block}$ 和全连接层(Output Layer)之后，$\hat{v}$ 的时间维度降到1，通道数映射到$C_i$ ，此时$\hat{v}\in\Bbb R^{1\times C_i}$ 将其视为第$k+1$ 时间步的预测值，用 MSE 作为损失函数：

$$\mathcal L(\hat{v};W_{\theta})=\Vert\hat{v}(v_{t-M+1},..,v_t,W_{\theta})-v_{t+1}\Vert^2$$

T-GCN

📑T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction

🧬T-GCN及其丰富的变种： https://github.com/lehaifeng/T-GCN

T-GCN将图卷积网络(GCN)和门控循环单元(GRU)结合起来，先通过前者学习空间拓扑结构，再通过后者学习数据的时间特征。具体来说，就是将时间步$t$ 的一次卷积得到的表示作为 GRU在时间步$t$ 时的表示，直到所有时间步的前向传播结束。如下图所示：

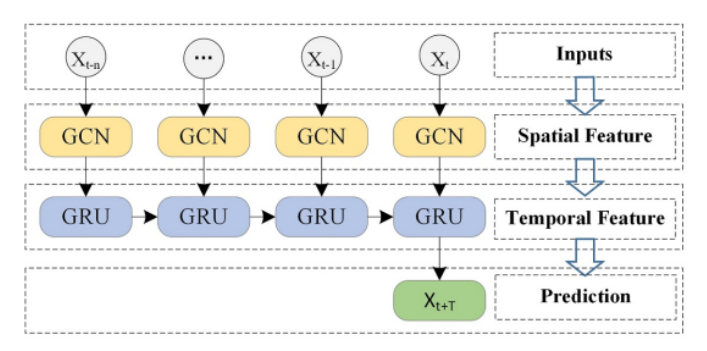
设$f(A,X_t)$ 为根据邻接矩阵$A$ 和时间步$t$ 时的特征$X_t$ 进行一次 GCN 的输出结果，则对应的门控循环单元的计算如下：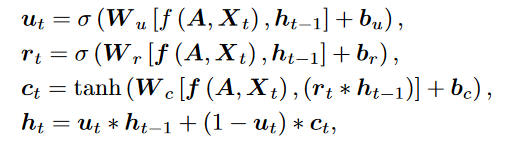

耦合神经架构

在耦合神经架构中，空间学习网络通常作为嵌入式组件集成到时间学习网络的架构中。在STGNN中，这种类型的神经结构几乎只出现在基于GNN的空间学习网络和基于RNN的时间学习网络的组合中。

DCRNN

📑Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting

🧬官方TensorFlow实现： https://github.com/liyaguang/DCRNN

DCRNN 使用双向随机游走来对空间依赖进行建模，使用encoder-decoder架构来对时间依赖进行建模，并在交通数据集 METR-LA 和 PEMS-BAY 上进行了测试，取得了很好的效果。

我们知道图上的扩散过程（也是随机游走过程）具体到有向图上是单向的。不过根据这篇论文的实际应用，作者考虑到使用两种方向的扩散过程（其实就是分别使用不同的权重$\theta_1,\theta_2$）。然后使用空域图卷积中的扩散卷积方法进行空间依赖的捕捉，即定义卷积操作：

$$\mathbf X_{:,p}*_{\cal G}\mathbf f_{\theta}=\sum_{k=1}^K\left(\theta_{k,1}(D_o^{-1}W)^k+\theta_{k,2}(D_i^{-1}W^\top)^k\right)\mathbf X_{:,p}$$

其中，$K$ 是扩散步数，$D_i,D_o$ 分别表示入度和出度矩阵，$W$为加权邻接矩阵，$P_1=D_o^{-1}W$ 为根据出度得到的正向概率转移矩阵，$P_2=D_i^{-1}W^\top$ 为根据入度得到的反向概率转移矩阵，$*_{\cal G}\;\mathbf f_\theta$ 表示参数为$\theta$ 的卷积算子。

假设输入通道/特征数为$P$，输出通道数为$Q$，那么卷积层的操作可以定义为：

$$\mathbf H_{:,q}=\alpha\left(\sum_{p=1}^P\mathbf X_{:,p}*_{\cal G}\mathbf f_{\Theta_{p.q}}\right),\qquad q\in\{1,2,..,Q\}$$

---

上面我们阐述了双向扩散卷积算子的运算过程，以及对应的图扩散卷积层的运算过程。接下来介绍的是 DCRNN 是如何运用上述卷积操作的。

DCRNN 将上一时间步得到的空间信息表示$H^{(t-1)}$ 与当前时间步的输入特征$X^{(t)}$ 结合起来共同作为GRU的特征，并且把GRU中的原始线性单元用图扩散卷积算子取代。该模块称为 DCGRU。

$$\begin{aligned} \boldsymbol{r}^{(t)}&=\sigma\left(\mathbf\Theta_r*_{\mathcal G}\left[\mathbf X(t),\mathbf H(t-1)\right]+\boldsymbol b_r\right)\\ \boldsymbol{u}^{(t)}&=\sigma\left(\mathbf\Theta_u*_{\mathcal G}\left[\mathbf X(t),\mathbf H(t-1)\right]+\boldsymbol b_u\right)\\ \tilde{\mathbf H}(t)&=\tanh\left(\mathbf\Theta_C*_{\mathcal G}\left[\mathbf X(t),(\boldsymbol r^{(t)}\odot\mathbf H(t-1))\right]+\boldsymbol b_c\right)\\ \mathbf{H}(t)&=\boldsymbol u^{(t)}\odot\mathbf H(t-1)+(1-\boldsymbol r^{(t)})\odot\tilde{\mathbf H}(t-1) \end{aligned}$$

---

在多步预测中，作者使用 Sequence to Sequence 架构。编码解码器都是 DCGRU。

• 训练时，把历史的时间序列放到编码器，使用编码器输出的最终状态初始化解码器。解码器生成预测结果。
• 测试时，ground truth 替换成模型本身生成的预测结果。

由于训练和测试输入的分布的差异会导致性能的下降，所以为了减轻这个问题的影响，作者使用了 scheduled sampling (Bengio et al., 2015)，在训练的第 $i$ 轮时，模型的输入要么是概率为 $\epsilon_i$ 的 ground truth，要么是概率为 $1-\epsilon_i$ 的预测结果。在训练阶段，$\epsilon_i$ 逐渐的减小为0，使得模型可以学习到测试集的分布。

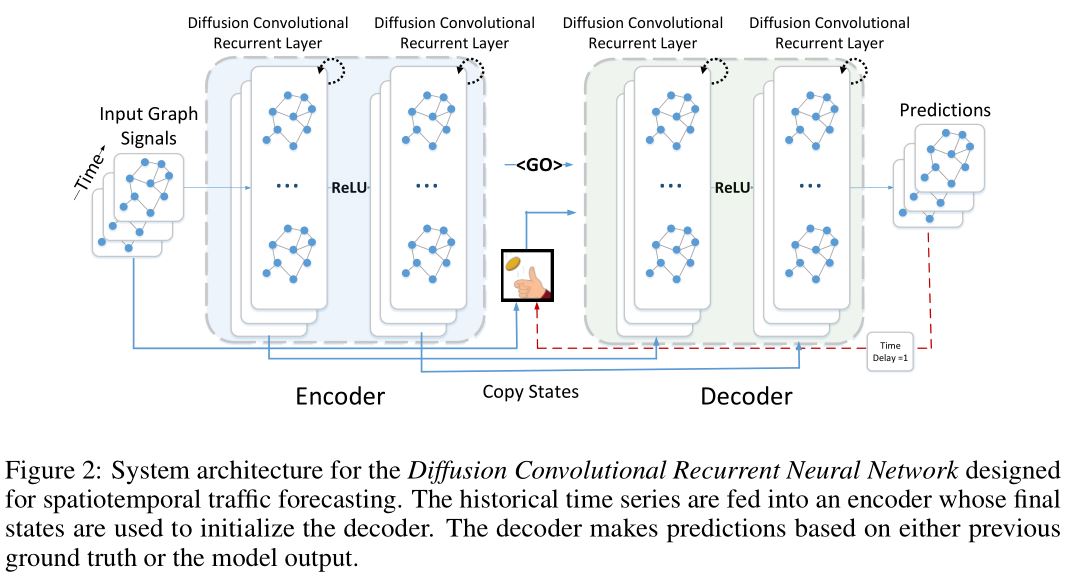
上图展示了 DCRNN 的架构。整个网络通过 BPTT 循环生成目标时间序列的最大似然得到。DCRNN 可以捕获时空依赖关系，应用到多种时空预测问题上。

EvolveGCN

• 【用GRU来学习GCN参数的新颖方法】EvolveGCN: Evolving Graph Convolutional Networks for Dynamic Graphs | 中文总结

Other Recurrent GCN

• 【提出因子型和耦合型两种架构】Structured Sequence Modeling with Graph Convolutional Recurrent Networks | 中文总结
• 【使用GCN+LSTM做图结构预测】 GC-LSTM: Graph Convolution Embedded LSTM for Dynamic Link Prediction | 中文总结
• 【GGNNs+LSTM做表示学习】 Learning to Represent the Evolution of Dynamic Graphs with Recurrent Models | 中文总结
• 【加入注意力机制的T-GCN】 A3T-GCN: Attention Temporal Graph Convolutional Network for Traffic Forecasting | 中文总结
• 【自适应GCN+GRU+独立参数】 Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting | 中文总结

Other Attention Aggregated STGNN

• 【三分支多粒度学习+时空注意力】Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting | 中文总结
• 【STAEformer：自适应+时空Transformer】STAEformer: Spatio-Temporal Adaptive Embedding Makes Vanilla Transformer SOTA for Traffic Forecasting | 中文总结
• 【PDFormer：延迟感知+多尺度注意力】PDFormer: Propagation Delay-aware Dynamic Long-range Transformer for Traffic Flow Prediction | 中文总结

参考

1. 时空图神经网络综述 - 知乎
2. STGCN论文详解 - 知乎
3. 论文笔记：DCRNN （Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting）-CSDN博客
4. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting - Davidham’s blog