大模型调参 μTransfer：Zero-Shot 的超参数迁移

📑 原始论文：Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer

研究背景

超参数（Hyperparameter，HP）调优一直是深度学习的关键步骤，但同样也是一个十分耗时耗力的过程。我们都知道如果 HP 选择不当，就会导致模型性能不佳、训练不稳定。特别是对于那些具有数十亿参数的神经网络大模型来说更是如此。

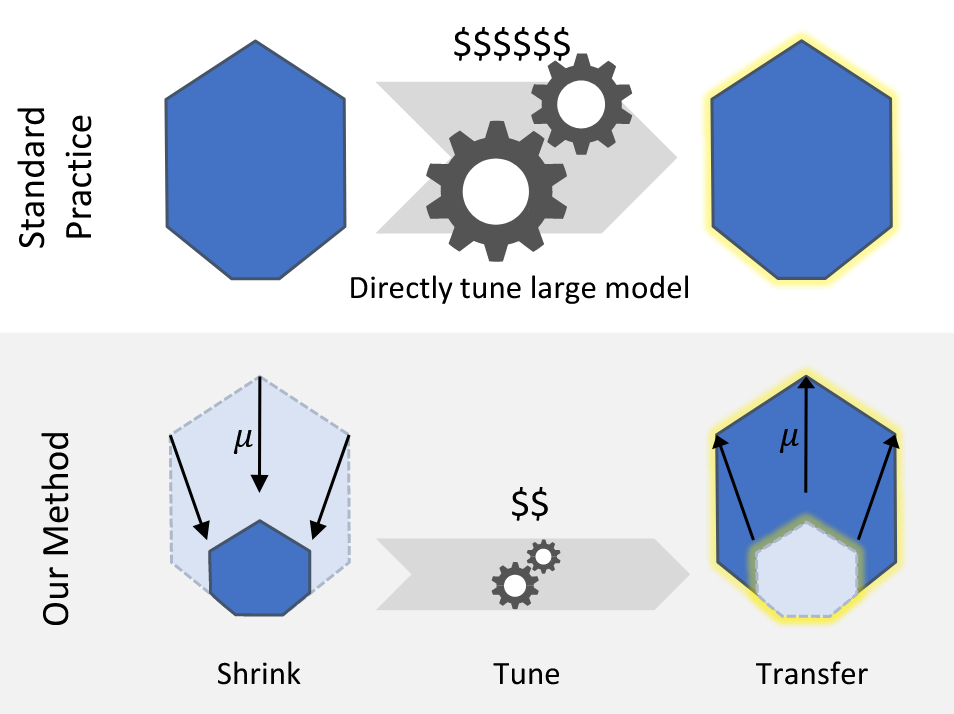
通过这项技术，我们可以实现先训练一个小规模的模型，在上面间接调优超参，然后以 zero-shot （零样本）的方式直接将这些超参迁移到大规模的模型上，就能获得相当不错的性能。

You can’t train GPT-3 on a single GPU, but you can tune its hyperparameters (HPs) on one.

最大更新参数化

muP (Maximal Update Parametrization) 是论文《Feature Learning in Infinite-Width Neural Networks》提出的一种特殊的神经网络参数化方法，旨在确保在无限宽度极限下，网络的每一层都能进行有效的特征学习。μTransfer 就是在 μP的基础上论证了其 zero-shot transfer HP to Large Model 的可行性。

先用实验说话。从上图可以看出，随着模型宽度 d_model （通常是指输入维度）的不同，使用传统的参数化方法（Standard Parametrization，SP）要使模型达到最优（Training Loss 最低），其学习率的设置不尽相同。而采用 muP 技术，可以保证不同宽度的模型最优时的学习率是稳定不变的。

下图的动图的方式再一次强调了这一点。

数学原理类比

根据中心极限定理（Central Limit Theorem，CLT），对于从均值为0，方差为1的分布中独立同分布抽样出来的 $n$ 个样本 $x_1,x_2,\cdots,x_n$ 来说，当 $n\to\infty$ 时，有：

$\frac1{\sqrt{n}}(x_1+x_2+\cdots+x_n)\sim\mathcal{N}(0,1)$

试想，如果我们定义函数 $F_n(c)=\mathbb{E}_{x}f(c(x_1+\cdots+x_n))$ ，其中 $f:\mathbb{R}\to\mathbb{R}$ 为有界的连续函数。与此同时，我们再定义函数 $G_n(\alpha)=F_n(\alpha/\sqrt{n})\to\mathbb{E}(\mathcal{N}(0,\alpha^2))$ ，记 $\alpha_n^*=\arg\min_{\alpha} G_n(\alpha)$ 是使得该函数最小化时的最优参数。

根据 CLT 我们可以自然地推导出当 $n\to\infty$ 时， $G_n(\alpha)$ 就是纯粹的以 $\alpha$ 为自变量的函数，而且它是收敛的。相反，原始的函数 $F_n(c)$ 随着 $c$ 的不同可能会发散。不仅如此，当 $n$ 足够大时，对任意 $N\gt n$ 都有 $\alpha_n^*$ 接近于 $\alpha_N^*$ .

类比过来也就是说，当我们想训练一个大模型，希望其损失最小化时，就相当于期望最小化函数 $F_N(c)=G_N(\alpha)$ 。此时，传统的参数化方法相当于是在对 $c$ 进行寻优，而 muP 技术则是在对 $\alpha$ 寻优。并且，前者得到的最优参数不具有随宽度变化的稳定性，即不可迁移到任意更大的 $N$ 的情况，而后者可以。

激活规模的稳定性

作者以单值线性投影 $f(x)=V^{\top}Ux$ 为例，简要说明了经过一层的隐藏层，然后利用 SGD 算法对参数 $V$ 和 $U$ 进行一次更新后，输出的分布范围。我们称之为 “activation scales”（激活规模）。

对于 SP 来说， $V\sim\mathcal{N}(0,1/n),\; U\sim\mathcal{N}(0,1)$ 。当学习率置 1 然后通过 SGD 算法对参数进行一次更新之后， $V'\leftarrow V+\theta U,\; U'\leftarrow U+\theta V$ . 这样一来，新的函数 $f$ 因为其表达式内含 $U^{\top}U=\Theta(n)$ 而产生爆炸。
对于 μP 来说， $V\sim\mathcal{N}(0,1/n^2),\; U\sim\mathcal{N}(0,1)$ ，并且学习率并不是统一缩放，具体来说 $\eta_V=1/n,,\; \eta_U=n$ . 所以一次更新之后原来的那一项变成了 $\theta n^{-1}U^{\top}U=\Theta(1)$ ，不会爆炸。

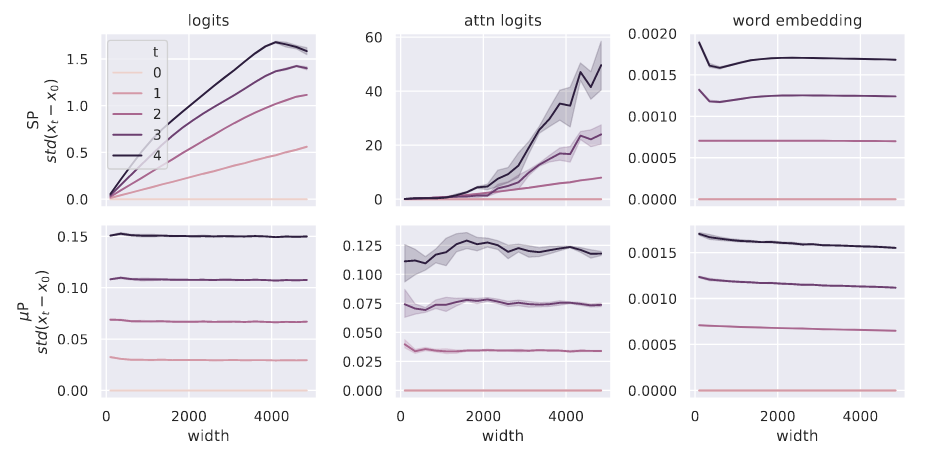
在利用 Transformer 模型做1 次到 5 次的更新的实验可以进一步说明该问题。与输入宽度有关是输出值 logits， attn logits 使用 SP 方法都产生了爆炸，而 μP 则相对很稳定。其中，word embedding 是与宽度无关的层，所以二者都比较稳定。

值得一提的是，作者还指出，SP 方法因为统一了学习率，所以“如果将学习率也按照宽度缩放不就能解决SP方法的迁移问题了吗？”的说法并不可行。因为这会导致不依赖于宽度的那些层（比如 Word Embedding）的更新也一同变得缓慢了，导致学习不到有用的信息。

哪些超参可以μP

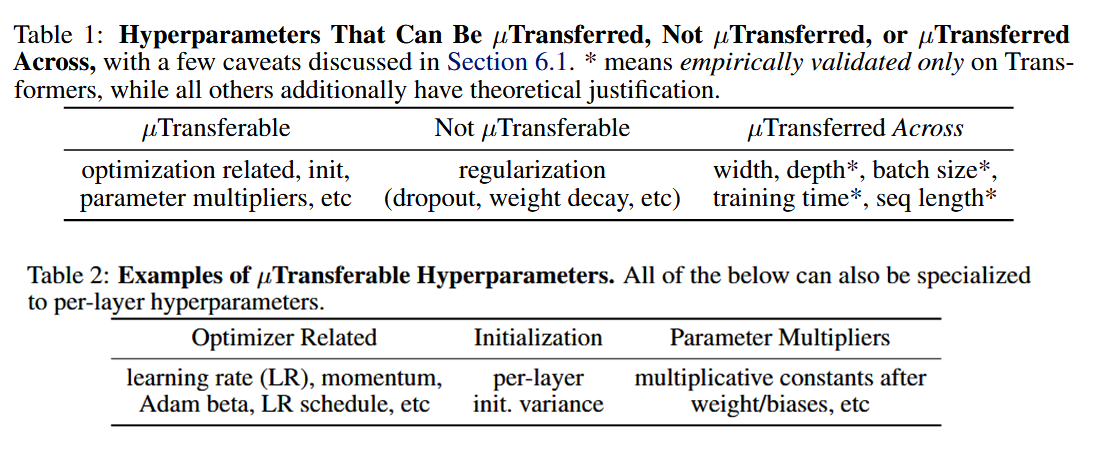
安装使用

安装 mup 库：

1	pip install mup

在代码层面，做如下调整：

将输出线性层替换为 MuReadout(...)
类Transformer模型，将注意力分数的缩放因子 $1/\sqrt{d}$ 更换为 $1/d$
（可选）使用 torchdistx 来避免直接实例化模型
确定参数的基本形状 set_base_shapes(...)
使用 mup 自带的参数初始化方法 mup.init 替代 torch.init
使用 mup 自带的优化器 mup.optim 替代 torch.optim

from mup import (MuReadout, 
				 make_base_shapes, 
				 set_base_shapes, 
				 MuSGD, 
				 MuAdam)

class MyModel(nn.Module):
    def __init__(self, width, ...):
        ...
        ### In model definition, replace output layer with MuReadout
        # readout = nn.Linear(width, d_out)
        readout = MuReadout(width, d_out)
        ### If tying weights with an input nn.Embedding layer, do
        # readout = MuSharedReadout(input_layer.weight)
        ...
    def forward(self, ...):
        ...
        ### If using a transformer, make sure to use
        ###   1/d instead of 1/sqrt(d) attention scaling
        # attention_scores = query @ key.T / d**0.5
        attention_scores = query @ key.T * 8 / d
        ### We use 8/d instead of 1/d here to be backward compatible
        ###   with 1/d**0.5 when d=64, a common head dimension.
        ...

### Instantiate(实例化) a base model
base_model = MyModel(width=1)
### Optionally, use `torchdistx.deferred_init.deferred_init` to avoid instantiating the parameters

### Simply install `torchdistx` and use
# base_model = torchdistx.deferred_init.deferred_init(MyModel, width=1)

### Instantiate a "delta" model that differs from the base model
###   in all dimensions ("widths") that one wishes to scale.
### Here it's simple, but e.g., in a Transformer, you may want to scale
###   both nhead and dhead, so the delta model should differ in both.
delta_model = MyModel(width=2) # Optionally use `torchdistx` to avoid instantiating

### Instantiate the target model (the model you actually want to train).
### This should be the same as the base model except 
###   the widths could be potentially different.
### In particular, base_model and model should have the same depth.
model = MyModel(width=100)

### Set base shapes
### When `model` has same parameter shapes as `base_model`,
###   `model` behaves exactly the same as `base_model`
###   (which is in PyTorch's default parametrization).
###   This provides backward compatibility at this particular model size.
###   Otherwise, `model`'s init and LR are scaled by μP.
### IMPORTANT: this should be called as soon as possible,
###   before re-initialization and optimizer definition.
set_base_shapes(model, base_model, delta=delta_model)

### Alternatively, one can save the base model shapes in a file
# make_base_shapes(base_model, delta_model, filename)
### and later set base shapes directly from the filename
# set_base_shapes(model, filename)
### This is useful when one cannot fit both 
###   base_model and model in memory at the same time

### Replace your custom init, if any
for param in model.parameters():
    ### If initializing manually with fixed std or bounds,
    ### then replace with same function from mup.init
    # torch.nn.init.uniform_(param, -0.1, 0.1)
    mup.init.uniform_(param, -0.1, 0.1)
    ### Likewise, if using
    ###   `xavier_uniform_, xavier_normal_, kaiming_uniform_, kaiming_normal_`
    ### from `torch.nn.init`, replace with the same functions from `mup.init`

### Use the optimizers from `mup.optim` instead of `torch.optim`
# optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
optimizer = MuSGD(model.parameters(), lr=0.1)

### Then just train normally