废话写在前

在计算机数据处理中，我们常常需要输出一个数组的最大值和最小值，乃至第kk 小值。

用数学语言来描述就是：
给定一个序列L=(a1,a2,...,an)L=(a_1,a_2,...,a_n) ，输出其第kk 大的元素a^\hat a ，它满足：

a^∈L,  ∑i=1nh(ai>a^)=k−1\hat a\in L,\;\sum_{i=1}^nh(a_i\gt\hat a)=k-1

其中，h(X)h(X) 为指示函数，有h(X)={1,X 为真,0,X 为假.h(X)=\begin{cases}1,&X\text{ 为真,}\\0,&X\text{ 为假.}\end{cases}

对于最值问题，一个最简单的选择算法就是顺序比较. 最坏情况下，时间W(n)=n−1W(n)=n-1.
如果需要同时找到最大和最小，最容易想到的就是两次顺序比较. 最坏情况下，时间W(n)=(n−1)+(n−2)=2n−3W(n)=(n-1)+(n-2)=2n-3.

以上的问题至少在本文章里就姑且称之为【最值选择问题】吧。
而同时选择出最大值和最小值就叫它【同时选择问题】。

此外，推广到更加一般的综合型的问题，即找第kk 大的问题我们称【一般选择问题】。
当然，最容易想到的方法是先对序列进行 排序 ，然后再取处对应下标kk 的元素即可。

本文将针对上述层层递进的三种问题的解决算法进行概述与分析。
其中【最佳选择问题】则是每一个程序员都会的顺序比较法，这里不再给出。这个方法的复杂度为Θ(n)\Theta(n)。
对于【同时选择问题】就更加巧妙一点，不再暴力查找，而是给出一个效率同比更高的分治策略方法。
对于【一般选择问题】我们先考虑一个【第二大选择问题】，因为它稍微特殊一点，可以利用锦标赛算法解决。然后的一般问题我们则会根据 快速排序 的思想提出 快速查找算法，以及其随机优化。另外再拓展给出一个对快排的改进版本，被称之为 BFPRT算法。其核心思想可以概括为“中位数的中位数”。

同时选择问题

二分裁决找最值

为了克服顺序比较这种暴力算法的时间性能较差的缺点，提出采用分治法进行优化。
其具体思想是：

  1. 将给定数组A[1..n]A[1..n] 每两个元素作为一组，共拆分为⌊n/2⌋\lfloor n/2 \rfloor 个组（nn 为奇数时多出一个元素，将其称为 轮空元素）；
  2. 每组进行比较，可得到⌊n/2⌋\lfloor n/2 \rfloor 个较大元素，⌊n/2⌋\lfloor n/2 \rfloor 个较小元素；
  3. 把轮空元素包含进⌊n/2⌋\lfloor n/2 \rfloor 个较大元素中，得到⌈n/2⌉\lceil n/2 \rceil 个元素组成的新数组，对其用同样的方法求分组最大，最终即可得到最大值；最小值同理。

利用递归的写法可以更好的体现上述步骤，我们把数组AA 拆为A[1..n/2],A[n/2+1..n]A[1..n/2],A[n/2+1..n]，即得到规模为n/2n/2 的两个子问题，求解得到两边的最值后，再进行比较就能得到AA 的最值。

算法的伪代码如下：

  • 输入：给定数组AA，左右边界l,rl,r （left, right）
  • 输出：数组AA 的最大值和最小值max,minmax, min

Algorithm:   Find-MaxMin(A,l,r)1.  if  l<r  then2.  mid←⌊(l+r)/2⌋3.  left-max,  left-min←Find-MaxMin(A,l,mid)4.  right-max,  right-min←Find-MaxMin(A,mid+1,r)5.  max←max(left-max,right-max)6.  min←min(left-min,right-min)7.  else8.  max←min←A[l]9.  return  max,min\begin{aligned} &\text{Algorithm: }\;\text{Find-MaxMin}(A,l,r)\\\\ 1.&\;\mathbf{if}\;l\lt r\;\mathbf{then}\\ 2.&\;\qquad mid\leftarrow \lfloor (l+r)/2\rfloor\\ 3.&\;\qquad left\text{-}max,\;left\text{-}min\leftarrow \text{Find-MaxMin}(A,l,mid)\\ 4.&\;\qquad right\text{-}max,\;right\text{-}min\leftarrow \text{Find-MaxMin}(A,mid+1,r)\\ 5.&\;\qquad max\leftarrow\text{max}(left\text{-}max,right\text{-}max)\\ 6.&\;\qquad min\leftarrow\text{min}(left\text{-}min,right\text{-}min)\\ 7.&\;\mathbf{else}\\ 8.&\;\qquad max\leftarrow min\leftarrow A[l]\\ 9.&\;\mathbf{return}\; max,min \end{aligned}

假设n=2kn=2^k ，则有W(n)=2W(n/2)+2,W(2)=1W(n)=2W(n/2)+2,W(2)=1，故：

W(2k)=2W(2k−1)+2=2[2W(2k−2)+2]+2=⋯=2k−1W(2)+(2+22+23+⋯+2k−1)=3n2−2\begin{aligned} W(2^k)&=2W(2^{k-1})+2\\ &=2[2W(2^{k-2})+2]+2\\ &=\cdots\\ &=2^{k-1}W(2)+(2+2^2+2^3+\cdots+2^{k-1})\\ &=\frac{3n}{2}-2 \end{aligned}

虽然时间复杂度仍可以记为O(n)O(n)，但比起暴力法系数变小了！当然其空间复杂度为O(1)O(1).

编程实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> FindMaxMin(vector<int> &A, int l, int r){
    vector<int> ans = {0,0};

    if(l < r){
        int mid = (l+r)>>1;
        vector<int> left = FindMaxMin(A, l, mid);
        vector<int> right = FindMaxMin(A, mid+1, r);

        ans[0] = max(left[0],right[0]);
        ans[1] = min(left[1],right[1]);
    }else{
        ans[0] = A[l];
        ans[1] = A[l];
    }
    return ans;
}

一般选择问题

快速选择算法

对于一般性选择问题，很容易想到先对整个数组进行 排序 ，然后再取下标kk 的元素。

而总览各种排序算法，首选的当属 快排。快排平均时间复杂度在O(nlog⁡n)O(n\log n)，有较好的快速性。然而再稍微分析其算法思路就知道，快排每一趟排序都使得所选的 枢轴位置 将小于它的元素和大于它的元素 划分在左右。然后再分别对左右两个子问题继续排序。

对于我们选择问题来说，我们并不需要得到排序结果，而只需要第kk 小的元素。因此可以直接在 快排 的源码上加上这样的判断策略：

【注】下面的算法都是根据需要找 第kk 小 而给出，当然这对 Top-K 问题同样适用，只需令k=n−k+1k=n-k+1 即可.

  1. 选出枢轴xx ，经一趟排序后确定其位置
    并划分出Al=A[p..q−1],  A[q]=x,  Ar=A[q+1..r]A_l=A[p..q-1],\;A[q]=x,\;A_r=A[q+1..r]
  2. 如果k≤∣Al∣k\leq|A_l| 即小于xx 的元素个数比kk 大，则继续在 子数组A[p..q−1]A[p..q-1] 中找第kk 小
  3. 如果k=∣Al∣+1k=|A_l|+1 说明所选的枢轴xx 即为第kk 小的元素，直接返回
  4. 否则，在 子数组A[q+1..r]A[q+1..r] 中找 第k−∣Al∣−1k-|A_l|-1 小

其中，∣S∣|S| 表示数组SS 的元素个数

经过上述分析，我们就可以得出快速选择算法的内容。

但是快排的缺点也同样被我们引入了进来，即当选取的枢轴使得数组划分不平衡时，会极大地影响算法效率。因此，参考快排的解决策略，这里我们也引入随机性，区别于直接将首元作为枢轴，我们对枢轴进行随机选取。

最终得到伪码如下：

Algorithm:   Randomized-Partition(A,p,r)1.  i←Random(p,r)2.  A[p]↔A[i]3.  x←A[p]4.  i←p;  j←r5.  while  i<j  do6.  while  i<j  and  A[j]>x  do7.  j←j−18.  while  i<j  and  A[i]≤x  do9.  i←i+110.  A[i]  ↔  A[j]11.  A[i]↔A[p]12.  return  i\begin{aligned} &\text{Algorithm: }\;\text{Randomized-Partition}(A,p,r)\\\\ 1.&\;i\leftarrow \text{Random}(p,r)\\ 2.&\;A[p]\leftrightarrow A[i]\\ 3.&\;x\leftarrow A[p]\\ 4.&\;i\leftarrow p;\;j\leftarrow r\\ 5.&\;\mathbf{while}\;i\lt j\;\mathbf{do}\\ 6.&\;\qquad\mathbf{while}\;i\lt j\;\text{and}\;A[j]\gt x\;\mathbf{do}\\ 7.&\;\qquad\qquad j\leftarrow j-1\\ 8.&\;\qquad\mathbf{while}\;i\lt j\;\text{and}\;A[i]\leq x\;\mathbf{do}\\ 9.&\;\qquad\qquad i\leftarrow i+1\\ 10.&\;\qquad A[i]\;\leftrightarrow\;A[j]\\ 11.&\; A[i]\leftrightarrow A[p]\\ 12.&\;\mathbf{return}\;i \end{aligned}

Algorithm:   Quick-Select(A,p,r,k)1.  if  p<r  then2.  q←Randomized-Partition(A,p,r)3.  if  k<q−p  then  return  Quick-Select(A,p,q−1,k)4.  elseif  k=q−p+1  then  return  A[q]4.  else  return  Quick-Select(A,q+1,r,k−q+p−1)\begin{aligned} &\text{Algorithm: }\;\text{Quick-Select}(A,p,r,k)\\\\ 1.&\;\mathbf{if}\;p\lt r\;\mathbf{then}\\ 2.&\;\qquad q\leftarrow \text{Randomized-Partition}(A,p,r)\\ 3.&\;\qquad\mathbf{if}\;k\lt q-p\;\mathbf{then}\;\mathbf{return}\;\text{Quick-Select}(A,p,q-1,k)\\ 4.&\;\qquad\mathbf{else if}\;k=q-p+1\;\mathbf{then}\;\mathbf{return}\;A[q]\\ 4.&\;\qquad\mathbf{else}\;\mathbf{return}\;\text{Quick-Select}(A,q+1,r,k-q+p-1)\\ \end{aligned}

BFPRT算法

我们知道，有序数组对于快排是“致命”的。如果不对快排做任何优化，那么在有序时将会达到O(n2)O(n^2). 同理，如果利用快速选择算法，在一遍遍迭代时，数组会变得有序，这极大降低了快速选择的执行效率。

为避免有序数组导致分组极度不平衡，除了引入随机之外，还有一种更好的策略。该策略与快排的思想整合，被称为 BFPRT选择算法。（俗称：中位数之中位数算法）

如下图所示，BFPRT算法先是将数组按每5个元素为一组进行分组，得到共⌊n/5⌋\lfloor n/5\rfloor 组。
然后分别对每一组进行排序（因为元素个数很少，可以利用快排处理）。
分别取出每一组的中位数共⌊n/5⌋\lfloor n/5\rfloor 个。由这些中位数构成的数组记为MM.

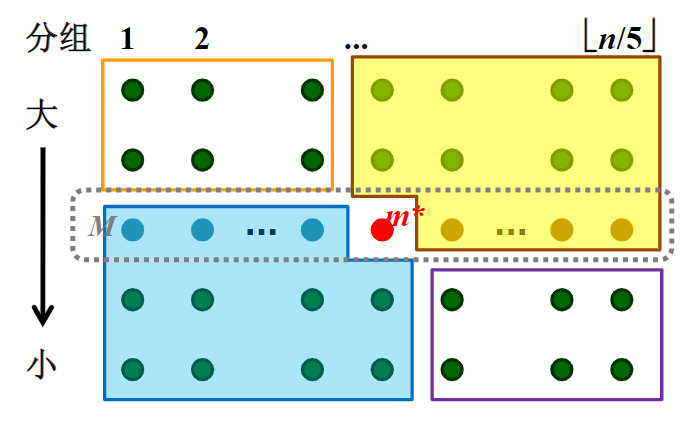
BFPRT分组

递归调用 BFPRT算法 ，对MM 求其中位数m∗m^*。此时递归所需的参数k=⌊n/5⌋/2k=\lfloor n/5\rfloor/2，表示找的是最中间的数，也就是中位数。

于是，m∗m^* 就是快速算法所需要的主元，即枢轴了。不仅如此，我们还可以快速地划分子数组。

如图所示，如果分组之后根据MM 进行的话（使得m∗m^*所在的组处于中心），那么图中左下角区域的元素均小于m∗m^*，右上角区域的元素均大于m∗m^*. 剩下的只需比较左上角和右下角即可。

对于元素个数小于 5 的子问题，直接利用快排求解；若不能整除，余下的小于 5 的元素自成一组，参与计算。

最终得到伪码：

  • 输入：数组AA，左右边界p,rp,r 以及kk
  • 输出：第kk 小的元素
  • 备注：QuickSort(),  Partition()\text{QuickSort}(),\;\text{Partition}() 的具体实现略过

Algorithm:   BFPRT(A,p,r,k)1.  n←r−p+12.  if  n<5  then3.  QuickSort(A,p,r)4.  return  A[p+k−1]5.  else6.  M←∅7.  G←⌊n/5⌋8.  repeat9.  对A[p..r]  分组为  A1=A[p..p+4],  A2=A[p+5..p+9],...9.  QuickSort(Ai)10.  M←M∪{Ai[mid−index]}11.  until  分组完毕12.  m∗←BFPRT(M,1,G,G/2)13.  根据 m∗划分子数组 Al,Ar  使得 A[q]=m∗14.  if  k<q−p  then  return  BFPRT(A,p,q−1,k)15.  elseif  k=q−p+1  then  return  m∗16.  else  return  BFPRT(A,q+1,r,k−q+p−1)\begin{aligned} &\text{Algorithm: }\;\text{BFPRT}(A,p,r,k)\\\\ 1.&\;n\leftarrow r-p+1\\ 2.&\;\mathbf{if}\;n\lt5\;\mathbf{then}\\ 3.&\;\qquad \text{QuickSort}(A,p,r)\\ 4.&\;\qquad \mathbf{return}\;A[p+k-1]\\ 5.&\;\mathbf{else}\\ 6.&\;\qquad M\leftarrow\varnothing\\ 7.&\;\qquad G\leftarrow\lfloor n/5\rfloor\\ 8.&\;\qquad \mathbf{repeat}\\ 9.&\;\qquad\qquad \text{对}A[p..r]\;\text{分组为}\;A_1=A[p..p+4],\;A_2=A[p+5..p+9],...\\ 9.&\;\qquad\qquad \text{QuickSort}(A_i)\\ 10.&\;\qquad\qquad M\leftarrow M\cup \{A_i[mid-index]\}\\ 11.&\;\qquad\mathbf{until}\;\text{分组完毕}\\ 12.&\;\qquad m^*\leftarrow\text{BFPRT}(M,1,G,G/2)\\ 13.&\;\qquad \text{根据 }m^*\text{划分子数组 }A_l,A_r\;\text{使得 } A[q]=m^*\\ 14.&\;\qquad\mathbf{if}\;k\lt q-p\;\mathbf{then}\;\mathbf{return}\;\text{BFPRT}(A,p,q-1,k)\\ 15.&\;\qquad\mathbf{else if}\;k=q-p+1\;\mathbf{then}\;\mathbf{return}\;m^*\\ 16.&\;\qquad\mathbf{else}\;\mathbf{return}\;\text{BFPRT}(A,q+1,r,k-q+p-1)\\ \end{aligned}

性能分析

当存在不够整除时，有不大于 5 的元素个数自成一组参与计算，此时数组AA 被我们分成了⌈n/5⌉\lceil n/5 \rceil 个组。出来自成的组和m∗m^* 所在的组外，至少有一半的组有 3 个元素是大于m∗m^* 的，有：

3(12⌈n5⌉−2)≥3n10−63\left(\frac 1 2\left\lceil\frac{n}{5}\right\rceil-2\right)\geq\frac{3n}{10}-6

因此，在伪代码第 14 ~ 15 行 的递归调用，至多作用于n−3n10+6\begin{aligned}n-\frac{3n}{10}+6\end{aligned} 个元素。
假设任何少于 140 个元素的输入需要O(1)O(1) 的时间，就可以得到递归式：

T(n)≤{O(1),n<140T(⌈n/5⌉)+T(7n/10+6)+O(n),n≥140T(n)\leq\begin{cases} O(1),&n\lt140\\ T(\lceil n/5\rceil)+T(7n/10+6)+O(n),&n\geq140 \end{cases}

那么，当n<140n\lt140 时，显然存在一个正常数cc 使得T(n)≤cnT(n)\leq cn ；
当n>140n\gt140 时，采用替换法，有：

T(n)≤c⌈n/5⌉+c(7n/10+6)+an≤cn/5+c+7cn/10+6c+an=9cn/10+7c+an=cn+(−cn/10+7c+an)\begin{aligned} T(n)&\leq c\lceil n/5 \rceil+c(7n/10+6)+an\\ &\leq cn/5+c+7cn/10+6c+an\\ &=9cn/10+7c+an\\ &=cn+(-cn/10+7c+an) \end{aligned}

此时，T(n)≤cnT(n)\leq cn 当且仅当−cn/10+7c+an≤0-cn/10+7c+an\leq0 当且仅当c≥10a[n/(n−70)]c\geq 10a[n/(n-70)]
由于假设有n≥140n\geq 140 ，因此取c≥20ac\geq 20a 就能够使得上述不等式成立。

综上所述，BFPRT算法 实现了最坏情况下时间复杂度为线性的选择，时间复杂度为O(n)O(n).
由于单开一个最长为n/5n/5 的数组，因此空间复杂度为O(n)O(n).

编程实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <cstdlib>

using namespace std;

int Partition(vector<int> &A, int p, int r){
    int i, j;
    i = p;
    j = r;
    int x = A[p];
    while(i < j){
        while(i < j && A[j] > x) j--;
        while(i < j && A[i] <= x) i++;
        swap(A[i],A[j]);
    }
    swap(A[p],A[i]);
    return i;
}

void QuickSort(vector<int> &A, int p, int r){
    if(p < r){
        int q = Partition(A, p, r);
        QuickSort(A, p, q-1);
        QuickSort(A, q+1, r);
    }
}

int BFPRT(vector<int> &nums, int l, int r, int k){
    int len = r-l+1;
    if(len <= 5){ //个数小于5时，直接快排取值
        QuickSort(nums, l, r);
        return nums[l+k-1];
    }
    int group = len/5; //分组个数(不含多余)
    vector<int> mids;
    for(int i = 0; i < group; i++){ //计算各分组的中位数
        QuickSort(nums, l+i*5, l+i*5+4);
        mids.push_back(nums[l+i*5+2]);
    }
    if(len%5 != 0){ //少于5的多余组
        QuickSort(nums, l+group*5, r);
        mids.push_back(nums[(l+group*5+r)/2]);
        group++;
    }
    int mid_key = BFPRT(mids, 0, group-1, (group+1)/2); //求出中位数的中位数

    //将主元放在第一个位置（因为Partition函数取第一个当主元）
    for(int i = l; i <= r; i++){
        if(nums[i] == mid_key){
            swap(nums[l],nums[i]);
            break;
        }
    }
    int mid_index = Partition(nums, l, r);

    if(l+k-1 == mid_index) return nums[mid_index];
    if(l+k-1 < mid_index) return BFPRT(nums, l, mid_index-1, k);
    else return BFPRT(nums, mid_index+1, r, l+k-mid_index-1);
}

int BFRPT_Select(vector<int> nums, int k){
    return BFPRT(nums, 0, nums.size()-1, k);
}

  

int main(void){
    vector<int> a = {8, 2, 3, 5, 7, 6, 11, 14, 1, 9, 13, 10, 4, 12, 15, 16};
    //依次输出第 i 小
    for(int i = 1; i <= a.size(); i++)
        cout << BFRPT_Select(a, i) << endl;
    return 0;
}

参考

  1. 《算法导论(原书第三版)》
  2. 算法设计与分析|中国大学MOOC
  3. 选择算法总结|CSDN