堆栈与队列及其应用|数据结构Ⅱ

堆栈

栈的基本概念

栈（Stack）是只允许在一端进行插入或删除操作的线性表。

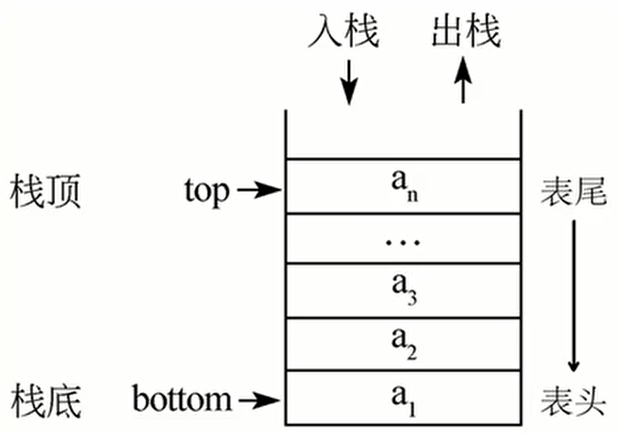
• 栈顶（Top）：线性表允许进行插入和删除的一端。

• 栈底（Bottom）：固定的，不允许进行插入和删除的另一端。

• 空栈：不含任何元素的空表。

假设某个栈$S=(a_1,a_2,\cdots,a_n)$ 如上图所示。
则$a_1$ 为栈底元素，$a_n$ 为栈顶元素。由于栈只能在栈顶进行插入和删除操作，故进栈次序依次为$a_1,a_2,\cdots,a_n$； 而出栈次序为$a_n,\cdots,a_2,a_1$。

栈的明显的操作特征为后进先出（Last In First Out，LIFO），故又称 后进先出的线性表。

栈的数学性质

对于$n$ 个不同元素按照不同的进栈方式，其出栈次序的可能种数为$\begin{aligned}\frac1{n+1}C_{2n}^{n}\end{aligned}$ .

下面我们仅给出递推式的推导，对其求解可得到结果正是上面给出的公式，这个公式我们称之为卡特兰数（Catalan）。
因为求解过程涉及到柯西乘积，感兴趣请移步到本站关于卡特兰数的相关文章继续深究。

假设$n$ 个元素的合法出栈顺序有$f(n)$ 种，自然有$f(0)=1,f(1)=1$.
此外，还假设进栈次序依次为$a_1,a_2,\cdots,a_n$。接下来我们讨论第一个进栈的元素$a_1$ 它有哪些出栈的可能即可。

若$a_1$ 在出栈序列中，排在第$k$ 个位置，我们可以据此把出栈序列以$a_1$ 为界限，一分为二：

$$Out=\{(a_{m_1},a_{m_2},\cdots,a_{m_{k-1}}),a_1,(a_{m_{k+1}},\cdots,a_{m_{n}})\}$$

对于在$a_1$ 之前出栈的那$k-1$ 个元素来说，因为入栈时$a_1$ 是第一个入栈的，所以这些元素的出栈次序不依赖$a_1$，是自由进出的一组序列；也就是它们的出栈次序正好就是一个子问题$f(k-1)$ 。

而对于$a_1$ 之后出栈的$n-k$ 个元素，$a_1$ 出去之后，它们的出栈次序也是自由的，所以也是一个子问题$f(n-k)$ 。

根据组合性原理，$a_1$ 排在$k$ 位置的所有可能的出栈次序个数就是$f(k-1)f(n-k)$.
遍历所有可能的$k$ 的取值，则有：

$$f(n)=\sum_{k=1}^n[f(k-1)f(n-k)]$$

卡特兰数的相关性质与证明见本站文章：算法与组合数学：卡特兰数

STL中的栈

C++ STL（标准模板库）是一套功能强大的C++ 模板类，提供了通用的模板类和函数，这些模板类和函数可以实现多种流行和常用的算法和数据结构，如向量、链表、队列、栈。

这里我们通过介绍 STL 中栈的基本操作，也顺便理清了栈的相关操作内容。前者在 ACM 比赛或是 算法机试中较为常用，所以此处一并介绍。

---

栈的创建

由于 stack 适配器以模板类 stack<T,Container=deque<T>>（其中 T 为存储元素的类型，Container 表示底层容器的类型）的形式位于 <stack> 头文件中，并定义在 std 命名空间里。
因此，在创建该容器之前，程序中应包含以下 2 行代码：

#include <stack>
using namespace std;

std 命名空间也可以在使用 stack 适配器时额外注明。

创建一个不包含任何元素的 stack 适配器，并采用默认的 deque 基础容器：

std::stack<int> values;

支持的成员函数

stack 是一类存储机制简单、提供成员函数较少的容器。下表列出了 stack 容器支持的全部成员函数。

成员函数	功能
empty()	当 stack 栈中没有元素时，该成员函数返回 true；反之，返回 false。
size()	返回 stack 栈中存储元素的个数。
top()	返回一个栈顶元素的引用，类型为 T&。如果栈为空，程序会报错。
push(const T& val)	先复制 val，再将 val 副本压入栈顶。这是通过调用底层容器的 push_back() 函数完成的。
push(T&& obj)	以移动元素的方式将其压入栈顶。这是通过调用底层容器的有右值引用参数的 push_back() 函数完成的。
pop()	弹出栈顶元素。
emplace(arg...)	arg... 可以是一个参数，也可以是多个参数，但它们都只用于构造一个对象，并在栈顶直接生成该对象，作为新的栈顶元素。
swap(stack<T> & other_stack)	将两个 stack 适配器中的元素进行互换，需要注意的是，进行互换的 2 个 stack 适配器中存储的元素类型以及底层采用的基础容器类型，都必须相同。

使用示例：

#include <iostream>
#include <stack>
#include <list>
using namespace std;
int main(){    //构建 stack 容器适配器
    list<int> values{ 1, 2, 3 };
    stack<int, list<int>> my_stack(values);    
    
    //查看 my_stack 存储元素的个数
    cout << "size of my_stack: " << my_stack.size() << endl;    
    
    //将 my_stack 中存储的元素依次弹栈，直到其为空
    while (!my_stack.empty()) {
        cout << my_stack.top() << endl; //将栈顶元素弹栈
        my_stack.pop();
    }
    return 0;
}

运行结果为：

size of my_stack: 3
3
2
1

栈的顺序存储

顺序栈 利用一组连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针 top 始终指向当前栈顶元素。（不同教材的定义有所不同）

#define MaxSize 100

typedef struct{
	ElemType data[MaxSize];
	int top;
}SqStack;

由于顺序栈的入栈操作受数组上界约束，所以对最大空间估计不足时，可能发生栈上溢。

基本操作的顺序栈实现

栈顶指针

void InitStack(SqStack &S){ // 初始化
	S.top = -1;
}

初始时，S.top 应置 -1，此时栈空；当 S.top == MaxSize-1 时栈满。

栈长：S.top+1
栈顶元素：通过 S.data[S.top] 访问得到。

入栈与出栈

/* 入栈 */
bool Push(SqStack &S, ElemType x){

	// 判满
	if(S.top == MaxSize-1) return false;
	
	//指针上移，并通过top进行赋值
	S.data[++S.top] = x; 
	return true;
}

/* 出栈 */
bool Pop(SqStack &S, ElemType &x){ //注意此处需要 &x

	// 判空
	if(S.top == -1) return false;
	
	//把栈顶元素赋给通过引用得来的x，然后指针下移
	x = S.data[S.top--]; 
	return true;
}

共享顺序栈

共享栈 是利用栈底的位置不变性，将两个顺序栈共享同一个一维数组空间的建栈策略。
假设两个栈分别为$S_1,S_2$，二者共享存储区$A[0..MaxSize-1]$ 。采用栈顶相向，迎面增长的方式进行存储，即栈底设置在两端、栈顶 向共享空间的中间延申。如下图所示：

我们规定 top1 == -1 表示$S_1$ 的栈空；top2 == MaxSize 表示$S_2$ 的栈空。
当且仅当二者的栈顶指针相邻，top2-top1 == 1 时，栈满。

（此规定不同教材的定义有所不同）

typedef struct{
	ElemType stack[MaxSize];
	int top[2]; //两个栈顶指针
}ShareStk;

ShareStk S; //建立全局共享栈变量

下面是共享栈的入栈与出栈的实现，通过传递形参标志 index 表名当前需要对左边还是右边的栈进行入栈或出栈。

/* 入栈 */
bool Push(int index, ElemType x){
	if(index < 0 || index >1) return false; //无效标志
	if(S.top[1] - S.top[0] == 1) return false; //栈满
	switch(index){
		case 0:
			S.stack[++S.top[0]] = x;
			break;
		case 1:
			S.stack[--S.top[1]] = x;
			break;
		default:
			return false;
	}
	return true;
}

/* 出栈 */
bool Pop(int index, ElemType &x){
	if(index < 0 || index >1) return false; //无效标志

	switch(index){
		case 0:
			if(S.top[0] == -1)
				return false; //栈空
			else
				x = S.stack[S.top[0]--];
			break;
		case 1:
			if(S.top[1] == MaxSize)
				return false; //栈空
			else
				x = S.stack[S.top[1]++];
			break;
		default:
			return false;
	}
	return true;
}

栈的链式存储

链栈 的优点是便于多个栈共享存储空间以及提高效率，并且不存在上溢。
链栈通常采用单链表实现，并且规定所有操作都在表头进行。

下面是以不预设头结点为前提的链栈类型描述。

typedef struct LinkNode{
	ElemType data;
	struct LinkNode *next;
} *LinkStack;

队列

队列的基本概念

队列（Queue）简称：队。也是一种操作受限的线性表。
要求只允许在表的一段进行插入（称为入队），而在表的另一端进行删除（称为 出队）。

特点：先进先出（First In First Out，FIFO）。

• 空队列：不含任何元素的空表。
• 队尾（Rear）：允许插入的一端。此时，队列中最靠近队尾的一个元素叫作队尾元素。
• 队头（Front）：允许删除的一端。相应的，最靠近队头的一个元素叫作队头元素。

STL中的队列

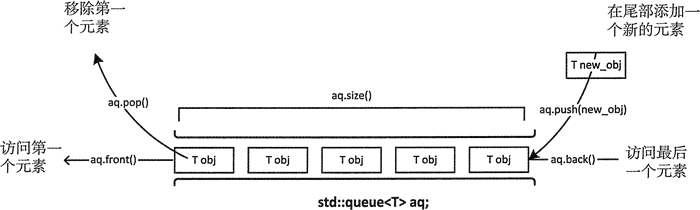
queue 容器适配器和 stack 的创建和操作都说类似的。并且有一些成员函数相似，但在一些情况下，工作方式有些不同。

成员函数	功能
empty()	如果 queue 中没有元素的话，返回 true。
size()	返回 queue 中元素的个数。
front()	返回 queue 中第一个元素的引用。如果 queue 是常量，就返回一个常引用；如果 queue 为空，返回值是未定义的。
back()	返回 queue 中最后一个元素的引用。如果 queue 是常量，就返回一个常引用；如果 queue 为空，返回值是未定义的。
push(const T& obj)	在 queue 的尾部添加一个元素的副本。这是通过调用底层容器的成员函数 push_back() 来完成的。
emplace()	在 queue 的尾部直接添加一个元素。
push(T&& obj)	以移动的方式在 queue 的尾部添加元素。这是通过调用底层容器的具有右值引用参数的成员函数 push_back() 来完成的。
pop()	删除 queue 中的第一个元素。
swap(queue<T> &other_queue)	将两个 queue 容器适配器中的元素进行互换，需要注意的是，进行互换的 2 个 queue 容器适配器中存储的元素类型以及底层采用的基础容器类型，都必须相同。

和 stack 一样，queue 也没有迭代器，因此访问元素的唯一方式是遍历容器，通过不断移除访问过的元素，去访问下一个元素。

下面这个例子中演示了表中部分成员函数的用法：

#include <iostream>
#include <queue>
#include <list>

using namespace std;
int main(){    //构建 queue 容器适配器
    std::deque<int> values{ 1,2,3 };
    std::queue<int> my_queue(values);//{1,2,3}
    //查看 my_queue 存储元素的个数
    cout << "size of my_queue: " << my_queue.size() << endl;
    //访问 my_queue 中的元素
    while (!my_queue.empty()) {
        cout << my_queue.front() << endl;  //访问过的元素出队列
        my_queue.pop();
    }
    return 0;
}

运行结果为：

size of my_queue: 3
1
2
3

队列的顺序存储

队列的顺序实现是指分配一块连续的存储空间存放队列元素，并且还需附设两个指针 front, rear 分别指向队头和队尾。
我们规定，rear 指向队尾元素的下一个位置；front 指向对头元素。（不同教材的定义有所不同）

#define MaxSize 100

typedef struct{
	ElemType data[MaxSize];
	int front, rear;
}SqQueue;

队指针

根据我们前面提到的规定，有：

• 初始状态：Q.front == Q.rear == 0
• 判空：Q.front == Q.rear
• 入队操作：队不满时，将值送到队尾所指处，队尾指针加1；
• 出队操作：队不空时，取出队头元素，队头指针加1。

void InitQueue(SqQueue &Q) { // 初始化
	Q.front = Q.rear = 0;
}

bool isEmpty(SqQueue Q){ //判空
	if(Q.front == Q.rear) return true;
	else return false;
}

注意，我们并不能用 Q.rear == MaxSize 来作为判满条件。
原因是我们对队列的入队出队处理是通过移动指针实现的，出队时，Q.front 会上移，如下图的 (d) 部分所示。此时入队会出现上溢出，但这种溢出是一种”假溢出“。

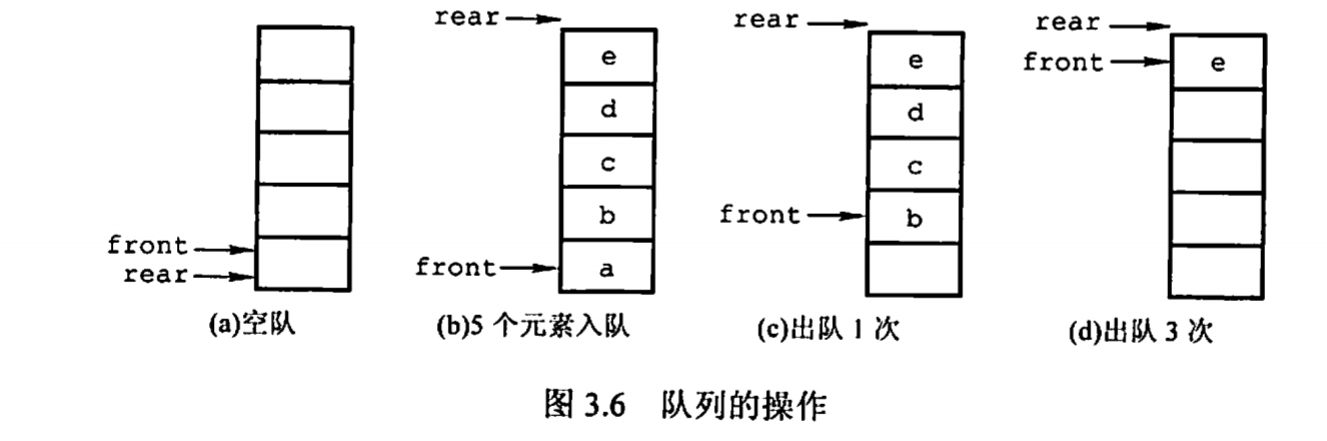
在真正介绍入队与出队的编程实现之前，我们也在图中发现了这种”假溢出“的缺陷。为了克服这种缺陷，我们将引入循环队列的思想。

循环队列

我们知道，当队头和队尾指针在经过复数次出队入队后，它们的位置可能会移动到数组较后的位置，此时前面的空闲空间将得不了使用，也就是前面给出的图示那样，之后还会出现假溢出问题。

为了解决这个问题，我们将顺序队列臆造为一个环状的空间，使得存储队列元素的表从逻辑上成为一个环，这样的队列就是循环队列。

最简单的实现方法就是当队首指针 Q.front == MaxSize-1 之后，若它再前进，就把它调整到 0 的位置。这可以直接用模运算实现！

1. 初始时：$Q.front=Q.rear=0$
2. 队首指针进1：$Q.front\leftarrow(Q.front+1)\mod n$
3. 队首指针进1：$Q.rear\leftarrow(Q.rear+1)\mod n$
4. 队列实际长度：$(Q.rear-Q.front+n)\mod n$

其中，$n$ 是开辟的连续空间的单位个数，即 MaxSize

---

那么如何判断队满呢？

之前我们规定队空条件是 Q.front==Q.rear。但对于循环队列来说，当元素的入队速度高于出队速度时，就会出现队尾指针在环内追赶上队首指针的情况，此时 Q.front==Q.rear 成立，我们就无法判断当前是队空还是队满了。如下图 (d1) 所示。

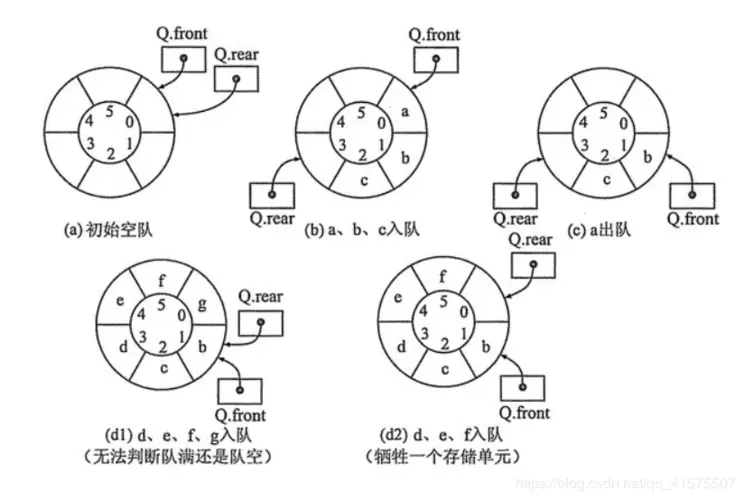
区分队空还是队满，可采用如下三种处理方法。

方法一 我们 **约定：队头指针指向队尾的下一个位置时队满** ，这样将牺牲一个存储单元，但也是较为普遍的实现方法。如上图 (d2) 所示。

于是，队满条件就是 (Q+rear+1)%MaxSize == Q.front ，队空条件不变。

方法二 增设表示元素个数的数据成员 `size`，从而队空就是 `Q.size == 0`，队满就是 `Q.size == MaxSize` 方法三 增设标志 `tag`，因插入导致 `Q.front == Q.rear` 时。`tag` 置 `1`，表示队满，反之因删除导致时，置 `0` 表示队空。

入队与出队

我们利用普遍使用的方法一进行队满判断。

/* 入队 */
bool EnQueue(SqQueue &Q, ElemType x){

	// 判满
	if((Q.rear+1)%MaxSize == Q.front) return false;
	
	//入队，rear循环上移
	Q.data[Q.rear] = x; 
	Q.rear = (Q.rear+1)%MaxSize;
	return true;
}

/* 出队 */
bool DeQueue(SqQueue &Q, ElemType &x){ //注意此处需要 &x

	// 判空
	if(Q.front == Q.rear) return false;
	
	//把队头元素赋给通过引用得来的x，然后指针循环上移
	x = Q.data[Q.front];
	Q.front = (Q.front+1)%MaxSize; 
	return true;
}

队列的链式存储

队列的链式表示称为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表。

• 头指针指向队头结点；
• 尾指针指向队尾结点，也就是单链表的最后一个结点。（注意与顺序队列的不同）

typedef struct LinkNode{ //链表结点类型
	ElemType data;
	struct LinkNode *next;
}LinkNode;

typedef struct{ //链队列
	LinkNode *front, *rear;
}LinkQueue;

显然，
对于不带头结点的链表，当 Q.front == NULL && Q.rear == NULL 时，队空。
对于带头结点的链表，当 Q.front == Q.rear 时，队空。

并且，单链表表示的链队列特别时候数据元素变动比较大的情形，还不会出现队列溢出问题。

基本操作的链队列实现

下面描述的都是在带头结点的单链表上的实现，因为不带头结点往往需要处理特殊情况，而带上头结点后，插入与删除操作可以得到统一。

void InitQueue(LinkQueue &Q) { //初始化
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	Q.front->next = NULL;
}

bool isEmpty(LinkQueue Q) { //判空
	if(Q.front == Q.rear) return true;
	else return false;
}

void EnQueue(LinkQueue &Q, ElemType x){ //入队

	// 与顺序队列不同，此处无需判满
	
	LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
	s->data = x; s->next = NULL; // 建立新结点s
	
	Q.rear->next = s;
	Q.rear = s; //结点插入到尾部，尾指针后移
}

bool DeQueue(LinkQueue &Q, ElemType &x){ //出队

	if(Q.rear == Q.front) return false; //判空
	
	LinkNode *p = Q.front->next; //p指向队首结点
	x = Q.front->data; //队首结点的内容传给x
	Q.front->next = p->next; //p断链
	if(Q.rear = p){
		Q.rear = Q.front;
	} //若当前只有一个结点，则删除后队为空
	
	free(p);
}

利用两个栈模拟队列

现已知两个栈$S_1,S_2$ 可供使用，且其入栈、出栈、判空判满操作均以提供。
尝试利用两个栈实现模拟一个简单队列的入队出队与判空操作。

简单起见，我们利用 STL 标准库提供的 stack 容器作为“已知各种操作”的两个栈。考虑下面几种情况：

1. 入队。入队操作可简单进行，只需保证入队的元素无遗漏地存储在栈中即可，不妨就将$S_1$ 作为容器，存储入队元素。如果$S_1$ 满了，则在$S_2$ 为空的情况下先全部送入$S_2$ 再继续存储。
2. 出队。由于栈的出栈次序与队列的出队次序正好相反，所以我们把存放于$S_1$ 中的元素依次弹出（出栈）并放入$S_2$ 中。此时$S_2$ 的出栈次序就与普通队列一致了，我们只需把$S_2$ 栈顶元素弹出即可完成出队。但此前需先判断$S_2$ 是否为空，否则将会产生顺序混乱。
3. 判空。

前面我们使用的代码，包括链表与顺序表都是按照 C 语言的写法。
这里区别于此，我们采用 C++ 面向对象的编写方式给出示例，以展现更加多元的编程。由于 STL 中并没有对栈长做限制，所以这里我们人为进行判满处理。只是作为逻辑上的补充。

#include <stack>
#include <iostream>

#define MaxSize 100
using namespace std;

template <class T>
class Queue_by2stack {
	private: 
		stack<T> s1, s2;
		bool StackOverflow(int); //栈判满
	public:
		Queue_by2stack(T); //构造函数
		
		bool EnQueue(T); 
		T DeQueue(); //出队
		bool isEmpty(); //判空
};

template <class T>
Queue_by2stack<T>::Queue_by2stack(T x){
    s1.push(x);
}

template <class T>
bool Queue_by2stack<T>::StackOverflow(int flag){
	switch(flag){
		case 1: return s1.size() >= MaxSize ?true:false;
		case 2: return s2.size() >= MaxSize ?true:false;
		default: cout << "WARNING:无效栈号" << endl; return false;
	}
}

template <class T>
bool Queue_by2stack<T>::EnQueue(T x){ //入队
	T tmp;
	if(!StackOverflow(1)){
		s1.push(x); // S1未满就放S1
		return true;
	}
	if(StackOverflow(1) && !s2.empty()){
		cout << "ERROR:列满" << endl; //S1满但S2有值时，不能放到S2里
		return false;
	}
	if(StackOverflow(1) && s2.empty()){
		while(!s1.empty()){
			tmp = s1.top(); //弹出首元
			s1.pop(); //删除首元
			s2.push(tmp); //S1满S2空时，全部搬运到S2
		}
		s1.push(x);
	}
	return true;
}

template <class T>
T Queue_by2stack<T>::DeQueue(){ //出队
	T tmp;
	if(!s2.empty()){
		tmp = s2.top();
		s2.pop();
		return tmp; //S2有内容时直接出栈，即为出队
	}else if(s1.empty()){
		cout << "ERROR:队列为空" << endl;
		return false;
	}else{
		while(!s1.empty()){
			tmp = s1.top();
			s1.pop();
			s2.push(tmp);
		}
		tmp = s2.top();
		s2.pop();
		return tmp;
	}
}

template <class T>
bool Queue_by2stack<T>::isEmpty(){
	if(s1.empty() && s2.empty())
		return true;
	else
		return false;
}

双端队列

双端队列（Deque）是指允许两端都可以进行入和出队操作的队列。
deque 是 “double ended queue” 的简称。那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。
由此可见，Deque 其实就是 Queue 和 Stack 混合而成的一种特殊的线性表，完全可以参考之前面的 Queue, Stack 的实现来构建双端队列的实现。

• 输入受限的双端队列：允许在一段插入和删除，而另一端只允许删除
• 输出受限的双端队列：允许在一段插入和删除，而另一端只允许插入

若限定双端队列从某个端点插入的元素只能从该端点删除，则双端队列就蜕变为了栈底相邻接的栈（注意不是共享栈）。

堆栈在算术表达式的应用

中缀表达式|_{Nifix expression}

中缀表达式是一个通用的算术或逻辑公式表示方法。
顾名思义，中缀表达式要求将运算符置于操作数之间，这也是我们最熟悉的算术表达式。
如：8*(4-2)/2+5*3 等。

在计算中缀表达式的值的过程中，由于算术优先级等问题计算机需要借助堆栈技术进行处理，具体算法如下：

1. 建立两个栈分别存放运算符和操作数。（$NS$: number stack ;$OS$:operator stack ）
2. 从左到右依次读取表达式。
   • 若读取到运算符，将其与$OS$栈顶的运算符比较优先级，若栈顶的优先级更高，则将$OS$栈顶的运算符和$NS$前两个操作数弹出并进行计算，将结果放入$NS$
   • 若读取到操作数，直接入$NS$
3. 不断压栈执行（重复第2步），直到$OS$空了为止
4. 取出$NS$剩下的值（唯一），即为最终结果。

例：8*(4-2)/2+5*3

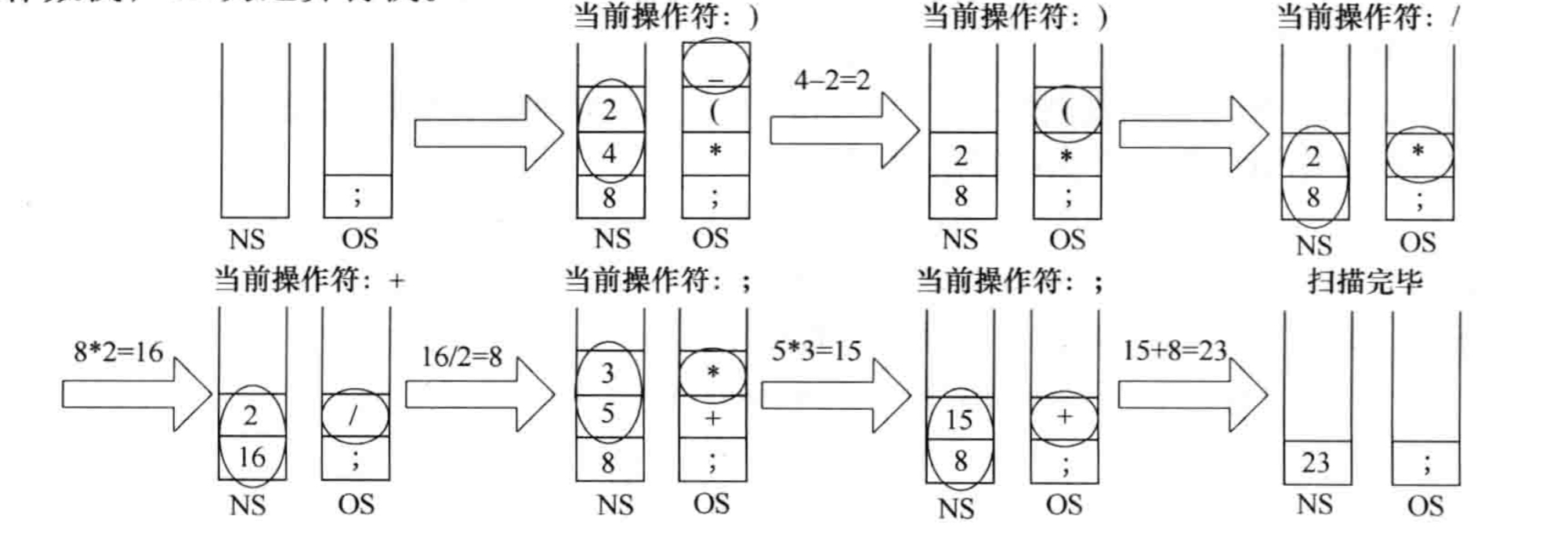
前缀表达式|_{Polish notation}

前缀表达式是一种没有括号的算术表达式，与中缀表达式不同的是，它将运算符写在前面，操作数写在后面。为纪念其发明者波兰数学家Jan Lukasiewicz，前缀表达式也称为“波兰式”($Polish\ notation$)

计算表达式的算法如下：

[要求从右往左读取，优点：只需要一个栈]

1. 依次读取操作数，当读到运算符时，将最近两个操作数进行计算，结果保存到栈之中；
2. 不断压栈执行（重复第1步），直到stack为止后停止；
3. 最后的输出值（弹出值），即为最终结果。

继续以前面的例子作为本次计算的基础，但是事先我们需要对表达式继续转化
即 将中缀表达式 转换为 前缀表达式

8 * ( 4 - 2 ) / 2 + 5 * 3$\to$ \+ / * 8 - 4 2 2 * 5 3

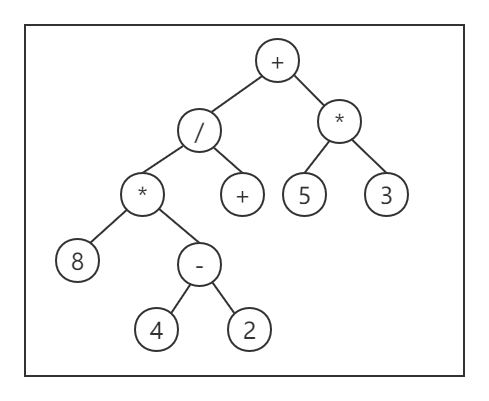
后缀表达式/逆波兰记法|_{RPN,Reverse Polish notation}

计算表达式的算法：与前缀表达式的计算法类似，改为从左至右即可

我们先将所需计算的 中缀表达式转为后缀：

$$\{\;8 * ( 4 - 2 ) / 2 + 5 * 3\;\} \to \{\;8\ 4\ 2\ -\ 2 \ /\ *\ 5\ 3\ *\ +\;\}$$

计算示例：

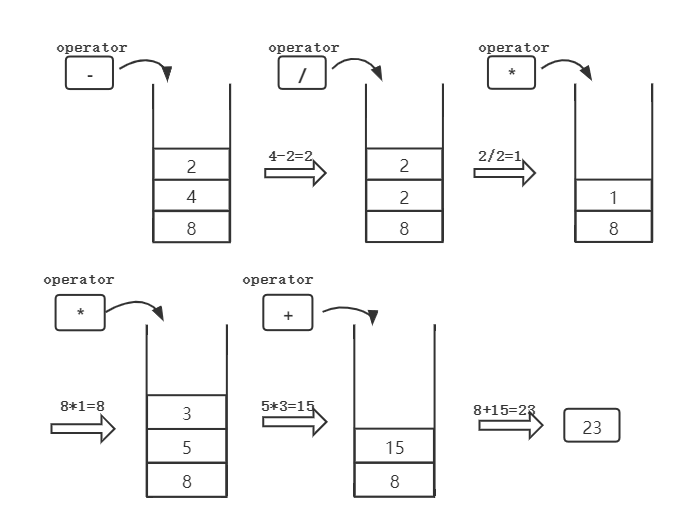
变换|_{Transformation}

前面我们反复提及将不同的表示方法相互转化。其中中缀转前缀和中缀转后缀的算法都十分类似，此处仅给出后者的算法以做示例。
算法包括手算和机算两种。

中缀转后缀 |手算

中缀转后缀的手算步骤如下：

1. 确定中缀表达式中各个运算符的运算顺序。

2. 选择下一个运算符，按照「左操作数 右操作数 运算符」的方式组合成一个新的操作数。

3. 如果还有运算符没被处理，就继续第 (2) 步。

继续以$8*(4-2)/2+5*3$ 为例：

第一步，先处理括号内的内容，把 (4 - 2) 调整为 4 2 - ；
第二步，处理除号，把 (4 2 -) 这个整体与 /后面的 2 作为操作数，调整得 4 2 - 2 /；
第三步，把 8 与第二步得到的 (4 2 - 2 /) 看作操作数，调整得 8 4 2 - 2 / *；
第四步，处理加号后面的 5 * 3 ，方法一样（也可以从加号处拆开，两边同时处理）。

最终得到如下结果：

$$\begin{aligned} Nifix=8 * ( 4 - 2 ) / 2 + 5 * 3\\\\ \Rightarrow 8 &* \{ 4\ 2\ -\} / 2 &+ \{5\ 3\ *\}\\ \Rightarrow 8 &* \{ 4\ 2\ - \ 2\ /\} &+ \{5\ 3\ *\}\\ \Rightarrow \{&8\ 4 \ 2\ -\ 2\ /\ *\}&+ \{5\ 3\ *\}\\\\ RPH=8\ 4\ 2\ -\ 2 \ /\ *\ 5\ 3\ *\ + \end{aligned}$$

中缀转后缀 |机算

创立$2$ 个栈：一个作为临时存储运算符的栈$S1$（含一个结束符号）；一个作为存放结果（逆波兰式）的栈$S2$（空栈）.
$S1$ 栈可先放入优先级最低的运算符#(可指定其他字符，不一定非#不可)

从中缀式的左端开始取字符，逐序进行如下步骤：

1. 若取出的字符是操作数则直接送入$S2$栈；

2. 若取出的字符是运算符，则：

   • 如果该运算符（不包括括号运算符）的优先级高于$S1$ 栈顶运算符（包括左括号）优先级，则将该运算符进$S1$ 栈；
     否则，将$S1$ 栈的栈顶运算符弹出，送入$S2$栈中，直至$S1$ 栈栈顶运算符（包括左括号）低于该运算符优先级时停止弹出运算符，再将该运算符送入$S1$ 栈；
   • 若取出的字符是(，则直接送入$S1$ 栈顶；
   • 若取出的字符是)，则将距离$S1$ 栈栈顶最近的(之间的所有运算符，逐个出栈，依次送入$S2$ 栈，此处抛弃(；
   • 若取出的字符是#，则将$S1$栈内所有运算符（不包括#），逐个出栈，依次送入$S2$栈。

3. 重复上述步骤，直至处理完所有的输入字符；

最终$S2$ 栈的内容便为逆波兰式输出结果（$S2$ 的输出需做逆序处理）

---

事实上，根据前面的描述，也可以通过构建二叉树并对二叉树进行先序遍历、后序遍历的方式实现，此为利用二叉树的算法。

关于二叉树的各类遍历将在我们后续介绍二叉树时重点阐述。

---

代码实现|_C++

待更

参考

1. 怎么理解出栈顺序有多少种？|知乎
2. 双端队列的实现（有图）|博客园
3. 算术表达式求解——堆栈的应用|Healist
4. 逆波兰式|百度百科
5. 数据结构.3 栈与队列 |CSDN