基本思想 在计算机科学中,分治法是一种很重要的算法。
字面上的解释是“分而治之 ”,就是把一个复杂的问题分成 两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解 ,原问题的解即子问题的解的合并 。
不难总结出分治策略的三大步骤:
分解|Divide 将原始问题划分或者归结 为规模较小的子问题解决|Conquer 递归或迭代求解每个子问题 合并|Combine 将子问题的解综合 得到原问题的解注意:
子问题应与原始问题性质完全一样 子问题之间可彼此独立地求解 递归停止时子问题可直接求解 对于分治法求解问题的分析,通常我们可以用递推式 ,又叫 递归式|Recurrence 来进行刻画。并且一般地,其递归式形如:
T ( n ) = ∑ i k a i T ( n − i ) + f ( n ) (1) T(n)=\sum_i^ka_iT(n-i)+f(n)\tag{1} T ( n ) = i ∑ k a i T ( n − i ) + f ( n ) ( 1 )
或:
T ( n ) = c T ( n / b ) + g ( n ) (2) T(n)=cT(n/b)+g(n)\tag{2} T ( n ) = c T ( n / b ) + g ( n ) ( 2 )
即 规模 为n n n 子问题 时间的线性组合,再加上非递归代价f ( n ) f(n) f ( n ) 用于分解和合并的代价 ,组成。
对于递归式的分析与计算,已在下面的本站文章中给出,此处从略。
改进措施 减少子问题个数 增加预处理 经典实例一览 排序问题类运用 二分查找问题 二分排序问题 归并排序问题 快速排序问题 移步👉🏻 排序算法全TIPS收集企划
快速选择类运用 最大最小选择问题 第k k k 线性时间选择问题 移步 👉🏻 选择算法也要收录
数学运用 最大子序和问题 最近点对问题 快速幂算法 大整数乘法问题 Stassen算法 FFT快速傅里叶变换 其他生活运用 汉诺塔问题 芯片测试问题 棋盘覆盖问题 循环赛日程表 最大子序和| Maximum Subarray 给定一个整数序列 L = ( a 1 , a 2 , . . . , a n ) L=(a_1,a_2,...,a_n) L = ( a 1 , a 2 , ... , a n ) 连续子序列 (子序列最少包含一个元素),返回其最大和。
不难写出,最大和的表示 :
max i , j { 0 , max 1 ≤ i ≤ j ≤ n ∑ k = i j a k } \max_{i,j}\left\{0,\max_{1\leq i\leq j\leq n}\sum_{k=i}^ja_k\right\} i , j max { 0 , 1 ≤ i ≤ j ≤ n max k = i ∑ j a k }
输入:整数序列 L = ( a 1 , a 2 , . . . , a n ) L=(a_1,a_2,...,a_n) L = ( a 1 , a 2 , ... , a n ) 输出:最大和 实例:最大子数组和|LeetCode 算法思想 假设给定序列L L L nums 进行存储,考虑如下的分治策略.
将数组n u m s [ l e f t . . r i g h t ] \boldsymbol{nums[}left..right\boldsymbol ] nums [ l e f t .. r i g h t ] m i d mid mi d 划分 为左右两个子数组:n u m s [ l e f t . . m i d ] , n u m s [ m i d + 1.. r i g h t ] \boldsymbol{nums[}left..mid\boldsymbol ],\quad \boldsymbol{nums[}mid+1..right\boldsymbol ] nums [ l e f t .. mi d ] , nums [ mi d + 1.. r i g h t ]
则原始问题的解只有3种情况:
由左子数组内的某个最大连续子数组 组成; 由右子数组内的某个最大连续子数组 组成; 横跨中心点 由某个最大连续子数组n u m s [ i . . m i d ] + n u m s [ m i d . . j ] \boldsymbol{nums[}i..mid]+\boldsymbol{nums[}mid..j\boldsymbol ] nums [ i .. mi d ] + nums [ mi d .. j ] 对于1,2两点,相当于是规模更小的同类子问题,可以直接递归实现 。从中心点出发往左右两边扩展 ,直到子数组的和最大。
算法伪码如下:
Algorithm: Find-Max-in-Mid ( n u m s , l e f t , m i d , r i g h t ) 1. l e f t - s u m ← − ∞ 2. s u m ← 0 3. f o r i = m i d d o w n t o l e f t d o 4. s u m ← s u m + n u m s [ i ] 5. i f s u m > l e f t - s u m t h e n 6. l e f t - s u m ← s u m 7. m a x - l e f t ← i 8. r i g h t - s u m ← − ∞ 9. s u m ← 0 10. f o r j = m i d + 1 t o r i g h t d o 11. s u m ← s u m + n u m s [ j ] 12. i f s u m > r i g h t - s u m t h e n 13. r i g h t - s u m ← s u m 14. m a x - r i g h t ← j 15. r e t u r n ( m a x - l e f t , m a x - r i g h t , l e f t - s u m + r i g h t - s u m ) \begin{aligned} &\text{Algorithm: }\;\text{Find-Max-in-Mid}(nums,left,mid,right)\\\\ 1.&\;left\text{-}sum\leftarrow-\infty\\ 2.&\;sum\leftarrow0\\ 3.&\;\mathbf{for}\;i=mid\;\mathbf{downto}\;left\;\mathbf{do}\\ 4.&\;\qquad sum\leftarrow sum+nums[i]\\ 5.&\;\qquad \mathbf{if}\;sum\gt left\text{-}sum\;\mathbf{then}\\ 6.&\;\qquad\qquad left\text{-}sum\leftarrow sum\\ 7.&\;\qquad\qquad max\text{-}left\leftarrow i\\ 8.&\;right\text{-}sum\leftarrow-\infty\\ 9.&\;sum\leftarrow0\\ 10.&\;\mathbf{for}\;j=mid+1\;\mathbf{to}\;right\;\mathbf{do}\\ 11.&\;\qquad sum\leftarrow sum+nums[j]\\ 12.&\;\qquad \mathbf{if}\;sum\gt right\text{-}sum\;\mathbf{then}\\ 13.&\;\qquad\qquad right\text{-}sum\leftarrow sum\\ 14.&\;\qquad\qquad max\text{-}right\leftarrow j\\ 15.&\;\mathbf{return}\;(max\text{-}left,max\text{-}right,left\text{-}sum+right\text{-}sum) \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Algorithm: Find-Max-in-Mid ( n u m s , l e f t , mi d , r i g h t ) l e f t - s u m ← − ∞ s u m ← 0 for i = mi d downto l e f t do s u m ← s u m + n u m s [ i ] if s u m > l e f t - s u m then l e f t - s u m ← s u m ma x - l e f t ← i r i g h t - s u m ← − ∞ s u m ← 0 for j = mi d + 1 to r i g h t do s u m ← s u m + n u m s [ j ] if s u m > r i g h t - s u m then r i g h t - s u m ← s u m ma x - r i g h t ← j return ( ma x - l e f t , ma x - r i g h t , l e f t - s u m + r i g h t - s u m )
Algorithm: Maximum-Subarray ( n u m s , l e f t , r i g h t ) 1. i f l e f t = r i g h t t h e n 2. r e t u r n n u m s [ l e f t ] 3. e l s e 4. m i d ← ⌊ ( l e f t + r i g h t ) / 2 ⌋ 5. l e f t - m a x ← Maximum-Subarray ( n u m s , l e f t , m i d ) 6. r i g h t - m a x ← Maximum-Subarray ( n u m s , m i d + 1 , l e f t ) 7. m i d - m a x ← Find-Max-in-Mid ( n u m s , l e f t , m i d , r i g h t ) 8. r e t u r n max ( l e f t - m a x , r i g h t - m a x , m i d - m a x ) \begin{aligned} &\text{Algorithm: }\;\text{Maximum-Subarray}(nums,left,right)\\\\ 1.&\;\mathbf{if}\;left=right\;\mathbf{then}\\ 2.&\;\qquad\mathbf{return}\;nums[left]\\ 3.&\;\mathbf{else}\\ 4.&\;\qquad mid\leftarrow \lfloor(left+right)/2\rfloor\\ 5.&\;\qquad left\text{-}max\leftarrow \text{Maximum-Subarray}(nums,left,mid)\\ 6.&\;\qquad right\text{-}max\leftarrow \text{Maximum-Subarray}(nums,mid+1,left)\\ 7.&\;\qquad mid\text{-}max\leftarrow \text{Find-Max-in-Mid}(nums,left,mid,right)\\ 8.&\;\qquad\mathbf{return}\;\max{(left\text{-}max,right\text{-}max,mid\text{-}max)} \end{aligned} 1. 2. 3. 4. 5. 6. 7. 8. Algorithm: Maximum-Subarray ( n u m s , l e f t , r i g h t ) if l e f t = r i g h t then return n u m s [ l e f t ] else mi d ← ⌊( l e f t + r i g h t ) /2 ⌋ l e f t - ma x ← Maximum-Subarray ( n u m s , l e f t , mi d ) r i g h t - ma x ← Maximum-Subarray ( n u m s , mi d + 1 , l e f t ) mi d - ma x ← Find-Max-in-Mid ( n u m s , l e f t , mi d , r i g h t ) return max ( l e f t - ma x , r i g h t - ma x , mi d - ma x )
时间复杂度 T ( n ) = 2 T ( n / 2 ) + Θ ( n ) T(n)=2T(n/2)+\Theta(n) T ( n ) = 2 T ( n /2 ) + Θ ( n ) 主定理 可以得出其时间复杂度为Θ ( n log n ) \Theta(n\log n) Θ ( n log n ) 编程实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 int maxInMid (vector<int >& nums,int left, int mid, int right) int left_sum = INT_MIN; int right_sum = INT_MIN; int sum = 0 , max_left = 0 , max_right = 0 ; for (int i = mid; i >= left; i--){ sum += nums[i]; if (sum > left_sum){ left_sum = sum; max_left = i; } } sum = 0 ; for (int j = mid+1 ; j <= right; j++){ sum += nums[j]; if (sum > right_sum){ right_sum = sum; max_right = j; } } return left_sum+right_sum; } int maxSubArrayReal (vector<int >& nums, int left, int right) if (left == right) return nums[left]; int mid = (left + right)/2 ; int left_max = maxSubArrayReal (nums, left, mid); int right_max = maxSubArrayReal (nums, mid+1 , right); int cross_max = maxInMid (nums, left, mid, right); return max (max (left_max,right_max),cross_max); } int maxSubArray (vector<int >& nums) return maxSubArrayReal (nums, 0 , nums.size ()-1 ); }
快速幂算法| Quick Power 最近点对问题| Closest pair of points 采用暴力算法需要对C n 2 C_n^2 C n 2 O ( d n 2 ) O(dn^2) O ( d n 2 ) O ( n log n ) O(n\log n) O ( n log n )
对于一维空间,我们可以用目前最好是排序算法先对数据进行排序,然后进行一次相邻点距离搜索即可得到结果,复杂度也在O ( n log n ) O(n\log n) O ( n log n ) d d d
这里我们只以二维空间为例,探讨如何利用分支方法处理二维平面的最近点对问题。
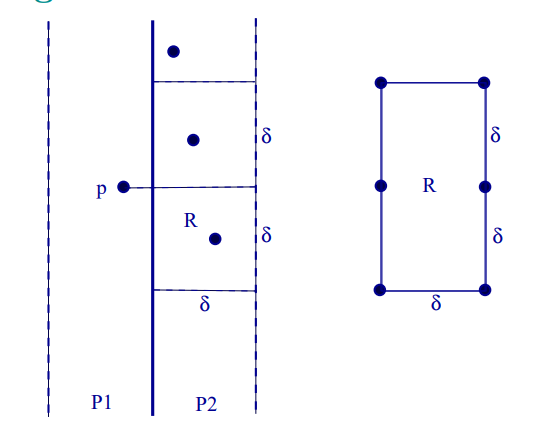
算法思想 将二维平面P P P 点个数大致相等 的两个平面P L , P R P_L,P_R P L , P R
Divide:作中垂线l l l P L , P R P_L,P_R P L , P R n / 2 n/2 n /2 S 1 , S 2 S_1,S_2 S 1 , S 2 Conquer:分别计算两个平面里面最近的点对δ 1 , δ 2 \delta_1,\delta_2 δ 1 , δ 2 Combine:计算两个平面之间的最近点对( p , q ) p ∈ S 1 , q ∈ S 2 (p,q)\quad p\in S_1,q\in S_2 ( p , q ) p ∈ S 1 , q ∈ S 2 δ c r o s s \delta_{cross} δ cross 取三个值中的最小值返回对应点对. 事实上,取δ = min ( δ 1 , δ 2 ) \delta=\min(\delta_1,\delta_2) δ = min ( δ 1 , δ 2 ) δ \delta δ δ c r o s s < δ \delta_{cross}\lt\delta δ cross < δ
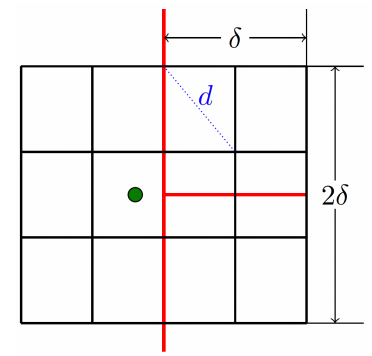
如图,以其中一个p ∈ S 1 p\in S_1 p ∈ S 1 δ \delta δ q ∈ S 2 q\in S_2 q ∈ S 2 δ × 2 δ \delta\times2\delta δ × 2 δ R R R
值得注意的是,如果将这个矩形按δ / 2 × 2 δ / 3 \delta/2\times2\delta/3 δ /2 × 2 δ /3 d = 5 δ / 6 < δ d=5\delta/6\lt\delta d = 5 δ /6 < δ δ \delta δ
也就是说,p p p 最多 只需要和6个q ∈ S 2 q\in S_2 q ∈ S 2 p p p q q q
事实上,如果我们对( l − δ , l + δ ) (l-\delta,l+\delta) ( l − δ , l + δ ) x x x y y y P L P_L P L P R P_R P R 计算该点与此后7个点的距离 。如果有小于δ \delta δ δ \delta δ
为什么是“此后”,不考虑“此前”?因为是按顺序遍历的,所以当前点之前的点已经把当前点与“此前”的距离计算一遍了。 为什么是7个点?与前面我们推出S 2 S_2 S 2 p p p δ \delta δ 另外,其实我们可以不必每一次都对点进行排序,只需在分治之前一次性先排序一次即可。这样一来我们便可以求出其时间复杂度:W ( n ) = T ( n ) + Θ ( n log n ) W(n)=T(n)+\Theta(n\log n) W ( n ) = T ( n ) + Θ ( n log n ) T ( n ) T(n) T ( n )
T ( n ) = 2 T ( n / 2 ) + O ( n ) ⇒ T ( n ) = O ( n log n ) T(n)=2T(n/2)+O(n)\Rightarrow\;T(n)=O(n\log n) T ( n ) = 2 T ( n /2 ) + O ( n ) ⇒ T ( n ) = O ( n log n )
编程实现 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 #include <iostream> #include <string.h> #include <vector> #include <cstdlib> #include <climits> #include <algorithm> using namespace std;long long min_d = INT64_MAX;struct Point { int id; int x,y; Point (){} Point (int _x, int _y){ x = _x; y = _y; } }; long long distence (Point a, Point b) if (a.id == b.id) return INT_MAX; return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y); } int cmp_with_x (Point a, Point b) if (a.x != b.x) return (a.x)<(b.x); else return (a.y)<(b.y); } Point CrossPart (Point *S, int mid, Point P_L, Point P_R, int l, int r) { long long Lmin = distence (S[P_L.x],S[P_L.y]); long long Rmin = distence (S[P_R.x],S[P_R.y]); long long delta = min (Lmin, Rmin); Point P; if (Lmin > Rmin) P = P_R; if (Lmin < Rmin) P = P_L; if (Lmin == Rmin){ if (S[P_L.x].id < S[P_R.x].id || (S[P_L.x].id == S[P_R.x].id && S[P_L.y].id < S[P_R.y].id)){ P = P_L; }else { P = P_R; } } vector<int > BarSet; for (int i = l; i <= r; i++){ if ((S[i].x-S[mid].x)*(S[i].x-S[mid].x) < delta){ BarSet.push_back (i); } } min_d = delta; long long temp_d; int a, b; for (int i = 0 ; i < BarSet.size (); i++){ for (int j = i+1 ; j < BarSet.size () && S[BarSet[j]].y <= S[BarSet[i]].y+delta; j++){ temp_d = distence (S[BarSet[i]],S[BarSet[j]]); if (temp_d > min_d) continue ; a = BarSet[i]; b = BarSet[j]; if (S[a].id > S[b].id) swap (a, b); if (temp_d == min_d){ if (S[a].id < S[P.x].id || (S[a].id == S[P.x].id && S[b].id < S[P.y].id)){ P.x = a; P.y = b; } }else { min_d = temp_d; P.x = a; P.y = b; } } } return P; } Point PartCacula (Point *S, int l, int r) { if (r - l + 1 < 3 ){ if (S[l].id > S[r].id) return Point (r, l); return Point (l, r); } int mid = l+(r-l+1 )/2 ; Point P_L = PartCacula (S, l, mid); Point P_R = PartCacula (S, mid+1 , r); return CrossPart (S, mid, P_L, P_R, l, r); } Point ClosestPair (Point* S, int n) { sort (S, S+n, cmp_with_x); return PartCacula (S, 0 , n-1 ); } #define CPC int main (void ) #ifdef CPC char bufin[40012 ],bufout[40012 ]; for (int k = 2 ; k <= 2 ; k++){ sprintf (bufin,"%02d.in" , k); sprintf (bufout,"%02d.out2" ,k); freopen (bufin,"rb" , stdin); freopen (bufout, "wb" , stdout); #endif int n, m; int i, j; while (scanf ("%d" , &n) != EOF){ Point* S = new Point[n]; for (int i = 0 ; i < n; i++){ S[i].id = i; scanf ("%d%d" , &S[i].x, &S[i].y); } Point res = ClosestPair (S, n); int id1 = S[res.x].id; int id2 = S[res.y].id; cout << id1 << " " << id2 << endl; cout << "=> distance: " << distence (S[res.x],S[res.y]) << endl; } #ifdef CPC } #endif return 0 ; }
大整数乘法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 #include <stdio.h> #include <string.h> #include <stdlib.h> #include <iostream> #include <algorithm> #include <vector> using namespace std;struct BigBinary { vector<int > x; bool neg; void Init () clear (); neg = false ;} BigBinary (){Init ();} int is_zero () for (int i = (int )x.size () - 1 ; i >= 0 ; i --) { if (x[i] == 0 ) x.pop_back (); else break ; } return x.empty (); } void Print () if (neg && !x.empty ()) printf ("-" ); for (int i = x.size () - 1 ; i >= 0 ; i--) printf ("%d" , x[i]); if (x.empty ()) printf ("0" ); printf ("\n" ); } }; BigBinary Add (BigBinary &a, BigBinary &b) BigBinary c; int jinwei = 0 , temp; for (int i = 0 ; i < std::max (a.x.size (), b.x.size ()); i ++){ if (i < a.x.size () && i < b.x.size ()) temp = a.x[i] + b.x[i] + jinwei; else if (i < a.x.size ()) temp = a.x[i] + jinwei; else temp = b.x[i] + jinwei; c.x.push_back (temp % 2 ); jinwei = temp / 2 ; } if (jinwei) c.x.push_back (jinwei); return c; } BigBinary Minus (BigBinary &a, BigBinary &b) BigBinary c; int jiewei = 0 , temp; for (int i = 0 ; i < a.x.size (); i ++){ if (i < b.x.size ()) temp = a.x[i] - b.x[i] - jiewei; else temp = a.x[i] - jiewei; if (temp < 0 ) {c.x.push_back (temp + 2 ); jiewei = 1 ;} else {c.x.push_back (temp); jiewei = 0 ;} } return c; } BigBinary Mul (BigBinary &a, BigBinary &b) BigBinary c; for (int i = 0 ; i < a.x.size () + b.x.size (); i ++) c.x.push_back (0 ); for (int i = 0 ; i < a.x.size (); i ++) for (int j = 0 ; j < b.x.size (); j ++) c.x[i + j] += a.x[i] & b.x[j]; int temp = 0 ; for (int i = 0 ; i < c.x.size (); i ++){ c.x[i] += temp; temp = c.x[i] / 2 ; c.x[i] = c.x[i] % 2 ; } c.is_zero (); return c; } void MulN2 (BigBinary &a, int n_2) for (int i = 0 ; i < n_2; i++){ a.x.insert (a.x.begin (),0 ); } } BigBinary FasterMul (BigBinary &a, BigBinary &b) if (a.x.size () <= 500 && b.x.size () <= 500 ){ return Mul (a, b); } int i, j, k; BigBinary A, B, C, D; BigBinary AC, BD, ApB, DpC, ApB_DpC; int n = max (a.x.size (), b.x.size ()); if (n%2 !=0 ) n++; if (n-a.x.size () > 0 ){ k = n-a.x.size (); for (int i = 0 ; i < k; i++) a.x.push_back (0 ); } if (n-b.x.size () > 0 ){ k = n-b.x.size (); for (int i = 0 ; i < k; i++) b.x.push_back (0 ); } for (i = 0 ; i < n/2 ; i++){ B.x.push_back (a.x[i]); D.x.push_back (b.x[i]); } for (j = n/2 ; j < n; j++){ A.x.push_back (a.x[j]); C.x.push_back (b.x[j]); } AC = FasterMul (A, C); BD = FasterMul (B, D); ApB = Add (A, B); DpC = Add (D, C); ApB_DpC = FasterMul (ApB, DpC); ApB_DpC = Minus (ApB_DpC, AC); ApB_DpC = Minus (ApB_DpC, BD); MulN2 (ApB_DpC, n/2 ); MulN2 (AC, n); ApB_DpC = Add (ApB_DpC, BD); ApB_DpC = Add (ApB_DpC, AC); return ApB_DpC; } #define CPC int main (void ) #ifdef CPC char bufin[40012 ],bufout[40012 ]; for (int k = 1 ; k <= 1 ; k++){ sprintf (bufin,"%02d.in" , k); sprintf (bufout,"%02d.out2" ,k); freopen (bufin,"rb" , stdin); freopen (bufout, "wb" , stdout); #endif int n; int i, j; char ch_a[40012 ], ch_b[40012 ]; BigBinary a, b, c; cin >> ch_a >> ch_b; for (int i = (int )strlen (ch_a) - 1 ; i >= 0 ; i --) a.x.push_back (ch_a[i] - '0' ); for (int i = (int )strlen (ch_b) - 1 ; i >= 0 ; i --) b.x.push_back (ch_b[i] - '0' ); c = FasterMul (a,b); c.Print (); #ifdef CPC } #endif return 0 ; }
Strassen算法 目前还有一个更佳的算法:Coppersmith-Winograd 算法 ,该算法的时间复杂度能到达O ( n 2.376 ) O(n^{2.376}) O ( n 2.376 ) FFT快速傅里叶变换 汉诺塔问题| Hanoi Algorithm: Hanoi ( A , C , n ) 1. i f n = 1 t h e n Move ( A , C ) / / 只有一个盘子时,直接 A→C 2. e l s e 3. Hanoi ( A , B , n − 1 ) 4. Move ( A , C ) 5. Hanoi ( B , C , n − 1 ) 6. r e t u r n \begin{aligned} &\text{Algorithm: }\;\text{Hanoi}(A,C,n)\\\\ 1.&\;\mathbf{if}\;n=1\;\mathbf{then}\;\text{Move}(A,C)\;//\text{只有一个盘子时,直接 A→C}\\ 2.&\;\mathbf{else}\\ 3.&\;\qquad \text{Hanoi}(A,B,n-1)\\ 4.&\;\qquad \text{Move}(A,C)\\ 5.&\;\qquad \text{Hanoi}(B,C,n-1)\\ 6.&\;\mathbf{return} \end{aligned} 1. 2. 3. 4. 5. 6. Algorithm: Hanoi ( A , C , n ) if n = 1 then Move ( A , C ) // 只有一个盘子时,直接 A→C else Hanoi ( A , B , n − 1 ) Move ( A , C ) Hanoi ( B , C , n − 1 ) return
容易分析得出,有T ( n ) = 2 T ( n − 1 ) + 1 , T ( 1 ) = 1 T(n) = 2 T(n-1) + 1,\;T(1) = 1 T ( n ) = 2 T ( n − 1 ) + 1 , T ( 1 ) = 1 T ( n ) = 2 n − 1 = Θ ( 2 n ) T(n)=2^n-1=\Theta(2^n) T ( n ) = 2 n − 1 = Θ ( 2 n )
芯片测试| Chip testing 棋盘覆盖| Tromino Puzzle 这里的棋盘覆盖问题,又称 L型覆盖,Tromino谜题等。
Tromino是一个由棋盘上的三个邻接方块组成的L型骨牌 。2 n × 2 n 2^n\times 2^n 2 n × 2 n
🎲通过该网站 可以游玩一个8 × 8 8\times 8 8 × 8 The Tromino Puzzle
循环赛日程表 代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> #include <string.h> #include <vector> #include <stack> #include <cstdlib> #include <climits> #include <cmath> #include <queue> #include <algorithm> using namespace std;int main (void ) int n, m; int i, j; while (scanf ("%d" , &n) != EOF){ vector<vector<int >> a (n+1 ,vector <int >(n+1 )); for (i = 1 ; i <= n; i++){ a[1 ][i] = i; } for (m = 1 ; m <= n/2 ; m = m*2 ){ for (i = m+1 ; i <= 2 *m; i++){ for (j = m+1 ; j <= 2 *m; j++){ a[i][j] = a[i-m][j-m]; a[i-m][j] = a[i-m][j-m]+m; a[i][j-m] = a[i-m][j]; } } } for (i = 1 ; i <= n; i++){ for (j = 2 ; j <= n; j++){ printf ("%d " , a[i][j]); } printf ("\n" ); } } return 0 ; }
参考 《算法导论 (原书第三版)》 《算法设计与分析 (第3版)》,陈慧南著 算法设计与分析|中国大学MOOC 最大子数组和|LeetCode CLRS Solutions|算法导论习题答案 Tromino Puzzle|Stonybrook大学课件 Closest pair of points|UCSB大学课件